实验二 典型环节MATLAB仿真及控制系统时域分析

目录

一、实验目的

二、实验原理

三、实验环境

四、实验内容

 五、核心代码和实验结果

第一题

比例环节G1(s)=1和G2(s)=2

惯性环节G1(s)=1/s+1和G2(s)=1/0.5s+1

积分环节G1(s)=1/s

微分环节G1(s)=s

比例+微分环节（PD）G1(s)=s+2和G2(s)=s+1

比例+积分环节（PI）G1(s)=1+1/s和G2(s)=1-1/2s

 第二题

问题1

问题2

第三题

 五、实验总结

---

一、实验目的

1. 熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法
2. 通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解
3. 定性了解各参数变化对典型环节动态特性的影响。

二、实验原理

1.比列环节的传递函数为

2.惯性环节的传递函数为

 

3.积分环节的传递函数为

 

4.微分环节的传递函数为

5.比列+微分环节的传递函数

 

6.比例+积分环节的传递函数

 

7.控制系统的稳定性是评价控制系统性能的重要指标之一，而使用时域分析法是一种常见的判定控制系统稳定性的方法。该方法主要基于控制系统的时域响应，通过分析系统的过渡过程、调节时间、超调量等参数来判断系统是否稳定。具体实验步骤如下：

1. 将控制系统连通性调至闭合状态，并在输入端施加阶跃输入信号。
2. 利用示波器等仪器来记录系统输出信号，以观察系统的过渡过程，包括上升时间、峰值时间和调节时间等参数。
3. 根据系统的过渡过程及输出信号的变化，分析系统的稳定性，常用的方法包括根轨迹、极点位置等分析方法。
4. 如果系统稳定，则输出信号会逐渐稳定在某一固定值附近，如果系统不稳定，则输出信号会发生不断震荡或越过一定幅度范围。

8.控制系统的动态性能是评价控制系统品质的重要指标之一，主要包括系统的上升时间、峰值时间、调节时间、超调量以及稳态误差等参数。而使用时域分析法是一种常用的分析系统动态性能的方法。该方法主要基于控制系统的时域响应，通过分析系统的响应曲线、波形和变化规律来评价系统的动态性能。具体实验步骤如下：

1. 将控制系统连通性调至闭合状态，并在输入端施加特定的输入信号。
2. 利用示波器等仪器来记录系统输出信号，以观察系统的响应曲线和波形，确定系统的各项动态参数。
3. 根据系统响应的曲线、波形和变化规律，分析系统的动态性能。常用的方法包括绘制阶跃响应曲线、振荡周期分析、频率响应分析等。
4. 根据分析结果，对系统进行优化设计和调节，以改善系统的动态性能。

三、实验环境

MATLAB、windows7操作系统

四、实验内容

第一题：对以下典型环节进行MATLAB仿真，输入信号为阶跃信号，用示波器展示输出结果。

第二题：用控制系统时域分析法判定系统稳定性

 第三题：用系统时域分析法分析系统动态性能

 五、核心代码和实验结果

第一题

• 比例环节G1(s)=1和G2(s)=2

 

• 惯性环节G1(s)=1/s+1和G2(s)=1/0.5s+1

 

• 积分环节G1(s)=1/s

 

• 微分环节G1(s)=s

 

• 比例+微分环节（PD）G1(s)=s+2和G2(s)=s+1

• 比例+积分环节（PI）G1(s)=1+1/s和G2(s)=1-1/2s

 

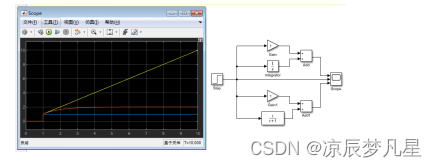
 第二题

问题1

问题2

 

第三题

 五、实验总结

通过这次接触MATLAB真正的体会到它强大的数值计算和符号计算功能，以及强大的数据可视化、人际智能交互能力。该工具主要处理以传递函数为主要特征的经典控制和以状态空间为主要特征的现代控制中的主要问题，它能够使图形生动形象的展现给我们，使理解更加深刻