典型环节的仿真实验（自控实验一）

实验目的     1）了解MATLAB Simulink的组成； 2）掌握线性系统Simulink仿真模型的建立方法； 3）通过典型环节阶跃响应的仿真，了解典型环节的动态特性； 4）了解MATLAB进行线性系统仿真的相关函数，编写线性系统仿真程序。

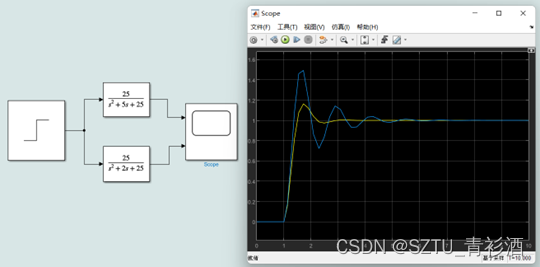
实验原理     1.典型环节 典型环节主要包括：比例环节（K）、积分环节（1s）、惯性环节（1Ts+1）、理想微分环节（s）、实际微分环节（0）和振荡环节（）等。各环节中特征参数的变化决定了系统具有不同的动态过程，例如：振荡环节的动态过程与其两个特征参数，即：自然频率和阻尼比有关。本实验主要任务之一是针对上述几种典型环节的传递函数，通过simulink仿真模型，观察各环节的动态响应特性，并分析动态过程随着参数变化而发生的改变。 2.matlab仿真程序 可以通过结构图的等效变换或者梅逊公式求解系统的传递函数，例如，可以求出下图中=      G1sG2(s)           1+G1sG2sHs+G1sG2(s)2；  =G2sG3s-(1+G1sG2(s)H(s))1+G1sG2sHs+G1sG2(s)   实际上当系统较为复杂时，也可以采用matlab程序的方式计算系统的传递函数，求解系统的零点、极点、增益等关键系统参数，以及分析系统的动态响应等等。本实验的另一个主要任务是，学习编写控制系统仿真及参数计算的matlab程序。相关matlab函数主要包括：tf(),zpk(),pzmap(),series(), parallel(), feedback(),impulse(),step()等。

实验条件     1）熟悉MATLAB的基本使用方法，了解MATLAB的基本数学函数及用法； 2）掌握典型环节的传递函数； 3）安装MATLAB（包括“Control System Tookbox”模块）的个人电脑。

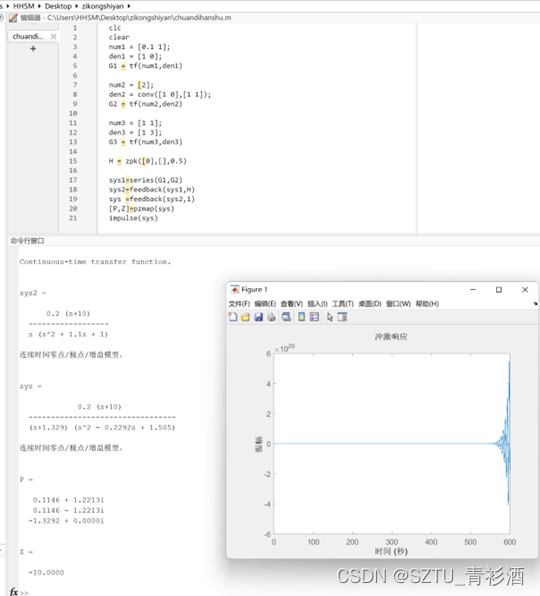
实验内容及记录 1.比例环节   Figure 1比例环节仿真模拟图 2.积分环节   Figure 2积分环节仿真模拟图 3.惯性环节   Figure 3惯性环节仿真模拟图 4.实际微分环节   Figure 4实际微分环节仿真模拟图 5.振荡环节 Figure 5振荡环节仿真模拟图（Wn不变）     Figure 6振荡环节仿真模拟图（ξ不变） 6.matlab控制系统仿真程序 (A) 用 tf 或 zpk 函数生成G1、G2、G3、H传递函数模型，其中 H 中令时间常数为0.5   Figure 7使用tf或zpk函数生成的传递函数模型 (B1)该传递函数的零点和极点 Figure 8该函数的零点与极点 (C1)改为1后，系统稳定   Figure 9改成1后，该系统稳定 (B2)该传递函数的零点和极点，可见下图   Figure 10该函数的零点和极点（见下图） (C2)改为1后，系统稳定   Figure 11改成1后，系统稳定

实验结果分析 1.对于典型环节方面的实验，有以下五个分析： ①比例环节：由以上阶跃响应波形图知，比例环节使得输出量与输入量成正比，既无失真也无延迟，响应速度快，能对输入立即做出响应，因此系统易受外界干扰信号的影响，从而导致系统不稳定。 ②积分环节：由以上阶跃响应波形图知，积分环节的输入量反映了输入量随时间的积累，积分作用随着时间而逐渐增强，其反映速度较比例环节迟缓。 ③惯性环节：由以上单位阶跃响应波形图知，惯性环节使得输出波形在开始时以指数曲线上升，上升速度与时间常数（当中的s的系数）有关。 ④实际微分环节：由以上单位阶跃响应波形图知，微分环节的输出反映了输入信号的变换速度，即微分环节能预示输入信号的变化趋势，若输入为一定值，输出为零。 ⑤振荡环节：由以上单位阶跃响应波形图知，振荡环节的图像与Wn和ξ有关，当Wn一定时，ξ与振荡峰值有关。当ξ一定时，Wn与振荡时间有关。 2. 对于matlab仿真程序方面的实验，有以下三个分析： ①可以通过matlab的tf和zpk函数生成传递函数。 ②可以通过matlab的程序求得函数的零点和极点。 ③可以通过matlab的程序来求得有一个输入时，该传递函数对应的响应图像。

结论及总结 本次实验我熟悉了matlab桌面和命令窗口，初步了解simulink功能模块的使用方法。Matlab中simulink是一个用来对动态系统进行建模、仿真和分析的软件包，利用simulink功能模块可以快速的建立控制系统的模型进行仿真和调试。 在实验中，我通过simulink功能模块建立控制系统各个典型环节的模型，进行仿真和调试，得到了各个典型环节在单位阶跃信号作用下的响应波形，通过观察各个典型环节在单位阶跃信号作用下的动态特性，我定性的了解各参数变化对典型环节动态特性的影响，同时也加深了我对各典型环节响应曲线的理解。此外，我还通过matlab仿真程序求得对应的响应图，我认为这一个实验是本次实验当中难度最大，也是用处最大的一个实验。

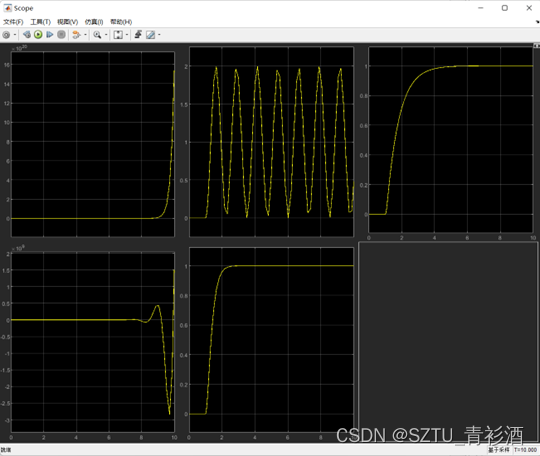
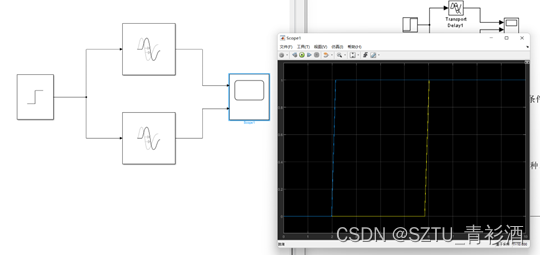
扩展实验及思考题     在中，令=-1、-0.5、0、1、2，=5，给出相应的传递函数，建立它们的阶跃响应的仿真模型，并分析其阶跃响应的特征。   Figure 12仿真图   Figure 13响应图 从左到右依次为ξ=-1、-0.5、0、1、2，对应的响应图。可以通过图像分析出改变ξ对函数的影响。 建立延迟环节的仿真模型，改变延迟时间，观察单位阶跃响应曲线变化情况。仿真框图如图所示。     Figure 14延迟环节仿真模型 积分环节能否用惯性环节近似？如果可以，近似的条件是什么？为什么？（可以以例子方式进行说明） 当时间常数趋于无穷大时，惯性环节可以近似地视为积分环节，当时间常数趋于0时，惯性环节可以近似地视为比例环节，可以根据公式推出。 某控制系统闭环传递函数,列举四种求闭环极点的matlab函数，并写出matlab求解程序。 % 以下是四个用于查找闭环极点的 MATLAB 函数： % 1. pole() % 此函数以传递函数或状态空间模型作为输入，并返回系统的极点。 function poles = find_poles(tf)     poles = pole(tf); end % 2. rlocus() % 此函数以系统作为输入，并绘制系统的根轨迹。根轨迹可用于查找闭环极点。 function rlocus_plot(sys)     rlocus(sys); end % 3. feedback() % 此函数以系统作为输入，并计算系统的闭环传递函数。闭环传递函数可用于查找闭环极点。 function closed_loop_tf = find_closed_loop_tf(sys)     closed_loop_tf = feedback(sys); end % 4. step() % 此函数以系统作为输入，并绘制系统的阶跃响应。 function step_plot(sys)     step(sys); end