模式识别与机器学习 学习笔记（三）

第二章   统计决策方法

目录

第二章   统计决策方法

一、贝叶斯决策基础知识

二、最小错误率贝叶斯决策

1. 基本思路

2.计算题（针对两类问题）

 三、最小风险贝叶斯决策

1. 基本思路

 2.计算例题（针对两类问题）

四、贝叶斯分类器设计

1.对于两类问题：

 2.对于多类问题：

3.计算例题

 五、正态分布时的统计决策

---

在学习贝叶斯决策方法之前，

我们需要先了解贝叶斯公式以及会出现在贝叶斯公式里的一些专有名词。

---

一、贝叶斯决策基础知识

1. 先验概率：   预先已知的或者可以估计的模式识别系统位于某种类型的概率。根据大量统计确定某类事物出现的比例。

如：  和    

2. 类条件概率：  类别状态为 时，样本 出现的概率密度

3. 全概率：   样本 在所有类别里出现的频率之和，也称为 的全概率；

4. 后验概率：   一个具体事物属于某种类别的概率；

    后验概率 涉及一个具体事物，而 先验概率 泛指一类事物；

5. 贝叶斯公式：

6. 两类决策问题中，可能犯两类错误：

第一类错误， 也称为 虚警（false alarm）

• 实际为  而错判为  。

•第一类错误率往往用  表示 。

•第一类错误率   

第二类错误， 也称为 漏报（missed detection）

•实际为  而错判为   。

•第二类错误率往往用 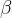 表示。

•第二类错误率   

7. 错误率 ：定义为所有服从同样分布的独立样本上错误概率的期 望，

即：               

                            

在实际应用中，常常通过下面的公式来计算分类错误率：

                     

                                 分类错误率=被错分的样本数/样本总数

8. 正确率 ：定义为所有服从同样分布的独立样本上正确概率的期 望，

即:

                                  

9. 贝叶斯决策 指的是在类条件概率密度和先验概率已知（或可以估计）的情况下，通过贝叶斯公式

比较样本属于两类的后验概率， 将类别决策为后验概率大的一类 ，这样做的目的是为了使总体错误率最小。

贝叶斯决策是基于贝叶斯公式

---

二、最小错误率贝叶斯决策

1. 基本思路

       在对样本进行决策时，从最小错误率的要求出发，利用概率论中的贝叶斯公式，得出使错误率最小的分类决策；也就是做出使后验概率最大的决策。

 最小错误率的贝叶斯准则对两类问题的决策规则：

如果  , 则  ; 反之，则 

在 多类情况下 ，最小错误率贝叶斯决策的原理是一样的，将 样本决策为后验概率最大的类别。

---

2.计算题（针对两类问题）

（1）

---

（2）

---

 三、最小风险贝叶斯决策

1. 基本思路

最小风险贝叶斯决策：是考虑各种错误造成损失不同的一种最优决策。

       具体如下：在采取每一个决策，都使其条件风险最小，则对所有的做出决策时，其期望风险也必然最小，这样的决策就是最小风险贝叶斯决策。

决策规则：若    ,  则  

 

---

 2.计算例题（针对两类问题）

（1）

---

（2） 

---

四、贝叶斯分类器设计

1.对于两类问题：

 2.对于多类问题：

---

3.计算例题

---

 五、正态分布时的统计决策

后续补充。。。