模式识别与机器学习学习笔记（四）

Rise9z

已于 2023-05-24 21:33:36 修改

阅读量530

点赞数 1

分类专栏：模式识别和机器学习文章标签：机器学习学习笔记

于 2023-05-24 21:31:06 首次发布

本文链接：https://blog.csdn.net/qq_63647674/article/details/130851699

版权

模式识别和机器学习专栏收录该内容

3 篇文章 1 订阅

订阅专栏

第三章、概率密度函数的估计

贝叶斯决策：利用类条件概率和先验概率来设计分类器；最核心的思想是利用后验概率；

贝叶斯决策的基础是概率密度函数的估计，即先验概率和类条件概率的估计。

第二章，在先验概率和类条件概率确定的情况下，我们通过贝叶斯公式来进行决策。

而第三章我们要解决的问题是估计先验概率 $P(\omega_{i})$ 和类条件概率 $P(x|\omega_{i})$

具体做法是：

利用训练样本估计先验概率和条件密度函数，并把这些估计的结果当作实际的先验概率和条件密度函数，然后再设计分类器。

二、最大似然估计与贝叶斯估计根本的区别（）

五、贝叶斯估计的基本原理（思路）、函数雅可比

一、概率密度估计的方法

1.参数估计

已知概率密度函数的形式，但其中部分或者全部参数未知，概率密度函数的估计问题就是用样本来估计这些参数，主要是方法有两大类：最大似然估计和贝叶斯估计 ，两者在很多实际情况下结果接近，但从概念上它们的处理方法是不同的。

2.非参数估计

就是概率密度函数的形式也未知，或者概率密度函数不符合目前研究的任何分布模型，因此不能仅仅估计几个参数，而是用样本把概率密度函数数值化的估计出来。

3.参数估计中的基本概念

统计量：每一种训练样本都包含着总体的某种信息，一个训练样本集包含总体的全部信息，针对不同的参数估计要求构造某种函数以便从样本集中抽取有关信息，这种函数称为统计量。

参数空间：所有未知参数的可能取值的集合称为参数空间，记为 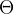$\Theta$ 。

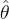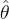点估计、估计量和估计值：估计总体分布的一个或几个具体参数叫点估计。针对某未知参数 $\theta$ 构造一个统计量作为 $\theta$ 的估计，称 $\hat{\theta}$ 为 $\theta$ 的估计量； $\hat{\theta}$ 的值叫做 $\theta$ 的估计值。

区间估计：除点估计外，还有另一类估计，他要求用区间 $(d_{1},d_{2})$ 作为 $\theta$ 可能取值范围的一种估计。这个区间称为 置信区间，这类估计问题称为 区间估计。

本章要求估计总体分布的具体参数，属于点估计问题。

我将介绍两种主要的点估计方法——最大似然估计和贝叶斯估计

二、最大似然估计与贝叶斯估计根本的区别（ $\bigstar$ ）

（1）最大似然估计是把待估计的参数当作未知但固定的量，要做的是根据观测数据估计这个量的取值；

（2）贝叶斯估计是把待估计的参数本身也看作是随机变量，要做的是根据观测数据对参数的分布进行估计，除了观测数据外，还可以考虑参数的先验分布。

三、最大似然估计的基本原理

已知某一类样本集包含 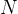$N$ 个样本 $\chi =\left \{ \right.x_{1},x_{2},\cdot \cdot \cdot ,x_{N}\left. \right \}$ ，带估计的未知参数为 $\theta$ ,由于假设样本是独立抽取的，那么

$l(\theta)=p(\chi |\theta)=p(x_{1},x_{2},\cdot \cdot \cdot ,x_{N}|\theta)=\prod_{i=1}^{N}p(x_{i}|\theta)$

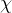看做是参数 $\theta$ 的函数，称联合概率密度 $p(\chi |\theta)$ 为样本集 $\chi$ 的似然函数，通常我们把这个函数用 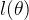$l(\theta)$ 来表示。

为了便于分析，由于对数函数的单调性，还可以定义对数似然函数：

$H(\theta)=\ln l(\theta)=\ln\prod_{i=1}^{N}p(x_{i}|\theta)=\sum_{i=1}^{N}\ln p(x_{i}|\theta)$

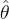
参数向量 $\theta$ 的最大似然估计，就是使 $p(\chi|\theta)$ 达到最大值的那个参数估计向量 $\hat{\theta}$

“最有可能出现的”样本 $\leftrightarrow {}$ 似然函数最大的样本

四、最大似然估计的求解（求均值、方差）

1. 求解方法：

根据已知的样本集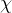 $\chi$ ，使似然函数 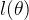$l(\theta)$ 取极大值 $\arg \max\ln l(\theta)$ 时得到的参数，

就是我们要找的估计量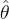 $\hat{\theta}$

2.计算例题

（1）

（2）

（3）

（4）

五、贝叶斯估计的基本原理（思路）、雅可比函数

1.基本原理（思路）

贝叶斯估计就是根据一个样本集 $\chi =\left \{ x_{1},x_{2},\cdot\cdot\cdot,x_{N} \right \}$ ,找出估计量 $\hat{\theta}$ ,估计 $\chi$ 所属总体分布的某个真实参数 $\theta$ ，使带来的贝叶斯风险最小。

具体来说，

就是利用先验概率 $p(\chi|\theta)$ 、类条件概率 $p(\theta)$ 和贝叶斯公式先求 $\theta$ 的后验概率密度函数 $p(\theta|\chi)$ ，然后，用 $\theta ^{*}=\int_{\Theta }^{}\theta p(\theta|\chi) d\theta$ ，即求在后验概率密度 $p(\theta|\chi)$ 下的期望值或平均值作为 $\theta$ 的估计。