编译原理——LR分析实验全过程+实验代码

一、实验目的

设计一个 LR 分析器，实现对表达式语言的分析，加深对 LR 语法分析方法的基本思想的理解，掌握 LR 分析器设计与实现的基本方法。

二、实验要求

建立文法及其 LR 分析表表示的数据结构，设计并实现一个 LALR(1)的分析器，对源程序经词法分析后生成的二元式代码流进行分析，如果输入串是文法定义的句子则输出“是”，否则输出“否”。

三、实验内容

（1）文法描述及其 LALR(1)分析表

描述表达式语言的文法 G 如下：

1. 1. S → E
   2. E → E+T
   3. E → T
   4. T → T*F
   5. T → F
   6. F → (E)
   7. F → ID

该文法的 LALR(1)分析表如下：

 

（2）LR 分析器总控程序框架

如下： 

（3）存放 LR 分析表的数据结构

① 实现方法一：用一个二维整数数组表示

数组元素为表示动作的整数。数组的行下标为状态号，列下标用来表示终结符与非终结符的整数表示。数组元素可作如下约定：

正整数：表示移进动作，如 S6 用数 6 表示；负整数：表示归约动作，如 R5 用数-5 表示；

0 ：表示接受，通常为按产生式 0 归约；状态号也用整数表示；

用不可能是状态号的较大的整数表示错误转移。

请将上述 LALR(1)分析表用这种表示方法，完成 LR 分析器的程序设计，并添加输出状态栈内容的功能。用上述表达式文法 G 的一个句子作为输入，进行测试。

② 实现方法二：采用压缩表示法

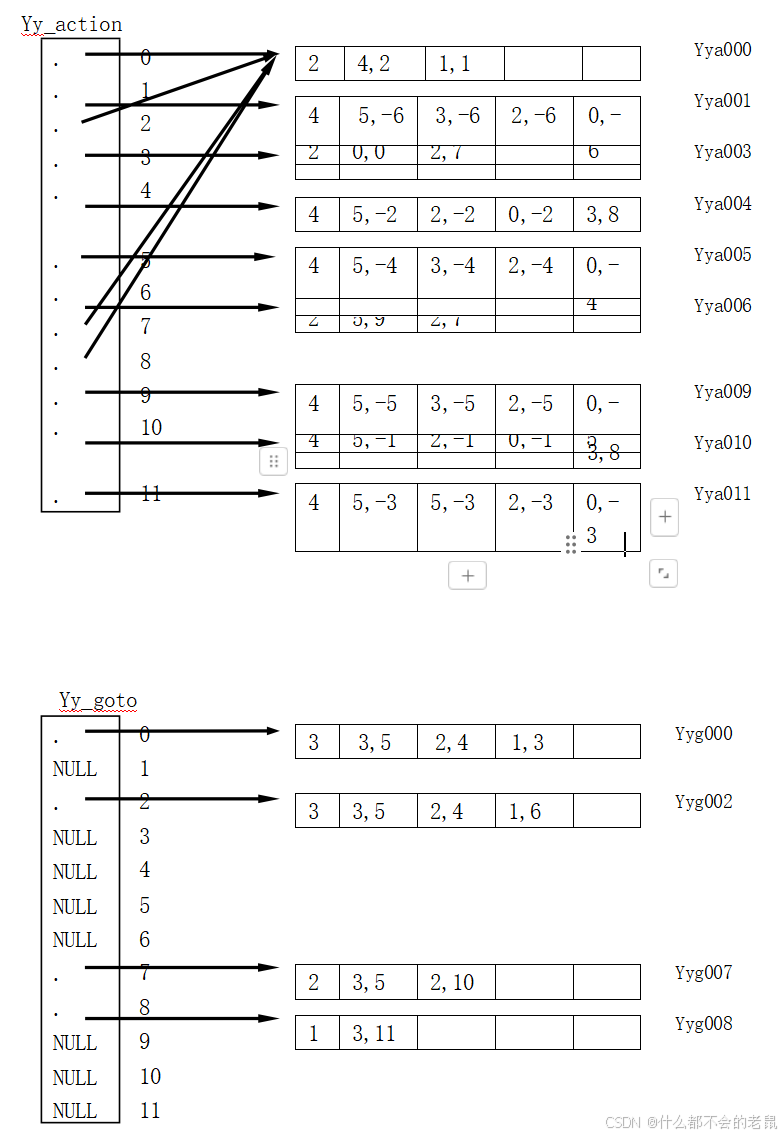
动作 Action 表的每一行用一个数组表示，数组的第一个元素是本数组中存放的数偶个数，第二个元素到最后一个元素都以[终结符，动作]的数偶的形式存放。再用一个以状态号为下标的下标数组，每个元素含一个指向数偶数组的指针。若数组元素的值为 NULL，则表示从此状态无转移弧发出。若分析表有几行相同，则只需保存一行，其它元素则都指向存放这一行表的数组即可。转移 Goto 表也按同样方式组织，只是这个行数组的数偶为[非终结符，下一状态号]。

每个行数组 Yyan 表示动作表 Yy_action 的一行，每个行数组 Yygn 表示转移表 Yy_goto 的一行。假定上述表达式文法 G 中终结符及非终结符的整数值为：

 

Yy_action 数组是以状态号为下标的下标数组，每个元素含有指向数组

Yyan 的指针；下标数组 Yy_goto 的每个元素含有指向数组 Yygn 的指针。表达式文法 G 的 LALR(1)分析表的具体压缩表示如下：

 

 

Yy_action

Yya009 Yya010 Yya011

 

 

 

 

 

 

 

Yyg000 Yyg002

 

 

 

 

Yyg007 Yyg008

 

 

 

 

 

以上分析表用 C 语言程序描述如下：

/*

* Yy_action 表

*/

int Yya000[]={2,4,2,1,1};

 

int Yya001[]={4,5,-6,3,-6,2,-6,0,-6}; int Yya003[]={2,0,0,2,7};

int Yya004[]={4,5,-2,2,-2,0,-2,3,8};

int Yya005[]={4,5,-4,3,-4,2,-4,0,-4}; int Yya006[]={2,5,9,2,7};

int Yya009[]={4,5,-5,3,-5,2,-5,0,-5};

int Yya010[]={4,5,-1,2,-1,0,-1,3,8};

int Yya011[]={4,5,-3,3,-3,2,-3,0,-3};

int Yy_action[]=

{

Yya000, Yya001, Yya000, Yya003, Yya004, Yya005, Yya006, Yya000, Yya000, Yya009, Yya010, Yya011

};

/*

* Yy_goto 表

*/

int Yyg000[]={3,3,5,2,4,1,3};

int Yyg002[]={3,3,5,2,4,1,6};

int Yyg007[]={2,3,5,2,10};

int Yyg008[]={1,3,11};

int Yy_goto[]=

{

Yyg000, NULL, Yyg002, NULL, NULL, NULL, NULL, Yyg007, Yyg008, NULL, NULL, NULL

};

/*

• 为了进行归约，使用一个 Yy_lhs[]数组，其值为代表产生式左部符

号的

• 整数，数组的下标为产生式号

*/

int Yy_lhs[7]=

{

 

		/*	0	*/	0,
		/*	1	*/	1,
		/*	2	*/	1,
		/*	3	*/	2,
		/*	4	*/	2,
		/*	5	*/	3,
		/*	6	*/	3
	};
/*

• Yy_reduce[]数组元素的值为产生式右部符号的个数，
• 以产生式号为数组的下标索引

*/

 

int Yy_reduce[]=

{

 

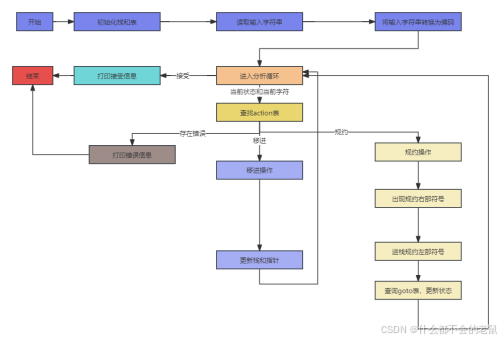
（4）实验流程图

（5）实验流程图解释

开始：程序启动

初始化栈和表：初始化状态栈和符号栈，以及goto表

读取输入字符串：从用户那里获取需要分析的字符串

将输入字符串转换为编码：将输入的字符串转换成对应的终结符和非终结符编码

初始化栈和指针：初始化栈的栈顶指针和活动指针

进入分析循环：开始循环分析过程

查找action表：根据当前状态和当前字符查找action表，确定是移进、规约还是接受

存在错误：如果查找到错误，则打印错误信息并结束

移进操作：如果是移进操作，更新栈和指针

规约操作：如果是规约操作，出栈规约右部符号，然后进栈规约左部符号，并查询goto表更新状态

打印接受信息：如果接受，则打印接受信息并结束

结束：程序结束

 

四、实验结果

对D+D*D该字符串分析的结果：

五、实验代码及注释

实验源代码：

#include <iostream> 
#include <cstring>  
#include <stack>    
#include <string>   
using namespace std; 

// 定义分析栈结构体
typedef struct analysisStack {
    int data[MAXSTACKSIZE]; // 栈内数据数组，存储栈中元素
    int top;               // 栈顶指针，指向栈内最后一个元素
} sqstack;

// 终结符集合，包括'#','D','+','*','(',')'
char VT[] = { '#', 'D', '+', '*', '(', ')' };
// 非终结符集合，包括'S','E','T','F'
char VN[] = { 'S', 'E', 'T', 'F' };
const int numVT = 6;  // 终结符数量
const int numVN = 4;  // 非终结符数量
const int stateNum = 12; // 状态数量，文法分析的状态机状态数
const int prodNum = 7; // 产生式数量，文法规则的数量

// 符号分析栈，用于存放输入字符串的终结符和非终结符
sqstack charStack;
// 状态分析栈，用于存放当前状态机的状态
sqstack stateStack;

// action表，用于存放对输入符号进行的动作，正数表示移进，负数表示规约，0表示接受
int action[stateNum][numVT] = {
    // ... 状态机的动作表，每个元素对应一个状态和一个终结符的动作
};

// goto表，用于状态转移，从当前状态根据输入的非终结符转移到新的状态
int gotoTable[stateNum][numVN];

// 记录每个产生式右部长度，即每个产生式右侧符号的个数
int reduceLen[prodNum] = { 1, 3, 1, 3, 1, 3, 1 };
// 记录每个产生式左部的非终结符编码，增加了100的偏移量，避免与终结符编码冲突
int leftProd[prodNum] = { 100, 101, 101, 102, 102, 103, 103 };

// 函数声明部分，声明了后面定义的函数原型
void process(string str, int strCode[]);
void strToNum(string str, int res[]);
void printContent(int charTop, int stateTop, string str, int ip);

int main() {
    // 初始化gotoTable，将所有元素设置为-1，表示未定义转移
    memset(gotoTable, -1, stateNum * numVN * sizeof(int));

    // 初始化goto表的特定元素，定义了特定状态下根据输入非终结符的转移状态

    // 从键盘读入需要分析的字符串，并添加结束符'#'
    string str;
    int strCode[MAX];
    cout << "请输入要分析的字符串:" << endl;
    cin >> str;
    str += '#'; // 添加结束符，以便进行语法分析
    strToNum(str, strCode); // 将输入字符串转换为终结符和非终结符的编码

    // 打印分析开始的提示信息
    cout << "开始分析..." << endl;
    for (int i = 0; i < 100; i++) cout << "-";
    cout << endl;
    cout << "stack(state)                   " << "stack(char)                    " << "input               " << "action          " << "goto" << endl;

    // 调用process函数开始语法分析过程
    process(str, strCode);
    return 0;
}

// 编码转换函数，将输入的字符串转换为终结符和非终结符的编码
void strToNum(string str, int res[]) {
    for (int i = 0; i < str.size(); i++) {
        switch (str[i]) {
            // 根据输入字符，将其转换为对应的终结符或非终结符编码
            case '(': res[i] = 4; break;
            case '+': res[i] = 2; break;
            case ')': res[i] = 5; break;
            case 'D': res[i] = 1; break;
            case '*': res[i] = 3; break;
            case '#': res[i] = 0; break;
            default:  res[i] = ERROR; // 无效字符，设置为ERROR
        }
    }
}

// 自下而上语法分析函数
void process(string str, int strCode[]) {
    // 初始化栈顶指针和活动指针
    stateStack.top = charStack.top = 0;
    stateStack.data[stateStack.top] = 0;  // 将文法开始状态0压入状态栈
    charStack.data[charStack.top] = 0;    // 将结束符'#'的编码0压入符号栈
    int ip = 0; // 初始化活动指针

    // 进入分析循环，直到分析结束或出现错误
    do {
        // 打印当前分析状态
        printContent(charStack.top, stateStack.top, str, ip);

        // 获取当前状态和当前字符对应的动作
        int state = stateStack.data[stateStack.top];
        int currentCode = strCode[ip];
        int currenAction = action[state][currentCode];

        // 根据当前动作进行相应的处理
        if (currenAction == ERROR || currentCode == ERROR || ip >= str.size()) {
            // 打印错误信息，结束分析
            for (int i = 0; i < 100; i++) cout << "-";
            cout << endl;
            cout << "分析语法错误!" << endl;
            break;
        } else if (currenAction > 0) {
            // 移进动作，将终结符对应的状态压入状态栈，并将符号压入符号栈，更新活动指针
            cout << "S" << currenAction << endl; // 打印移进动作编号
            stateStack.top++; // 状态栈压入新状态
            charStack.top++;  // 符号栈压入当前终结符编码
            stateStack.data[stateStack.top] = currenAction; // 压入新状态
            charStack.data[charStack.top] = currentCode;    // 压入当前终结符编码
            ip++; // 更新活动指针
        } else if (currenAction < 0) {
            // 规约动作，根据产生式编号进行规约
            cout << "R" << -currenAction << endl; // 打印规约产生式编号
            int len = reduceLen[-currenAction]; // 获取规约产生式的右部长度
            // 出栈规约右部符号，同时状态栈也要相应出栈
            for (int i = 0; i < len; ++i) {
                stateStack.top--;
                charStack.top--;
            }
            // 进栈规约左部符号的编码
            int left = leftProd[-currenAction];
            charStack.top++;
            charStack.data[charStack.top] = left;
            // 根据goto表查询下一个状态，并压入状态栈
            int top = stateStack.data[stateStack.top];
            int nextState = gotoTable[top][left - OFFSET];
            cout << nextState << endl; // 打印新状态
            stateStack.top++;
            stateStack.data[stateStack.top] = nextState;
        } else {
            // 接受状态，打印接受信息，结束分析
            cout << "ACC" << endl;
            for (int i = 0; i < 100; i++) cout << "-";
            cout << endl;
            cout << "结束分析" << endl;
            return;
        }

    } while (1); // 继续循环直到分析结束
}

// 打印当前分析情况的函数
void printContent(int charTop, int stateTop, string str, int ip) {
    // 打印状态栈内容，每个状态后面打印一个空格
    int stateLen = 0;
    for (int i = 0; i <= stateTop; ++i) {
        cout << stateStack.data[i] << " ";
        stateLen += to_string(stateStack.data[i]).size() + 1;
    }
    // 打印空格，使状态栈和符号栈对齐
    for (int i = stateLen; i < 31; ++i) cout << " ";

    // 打印符号栈内容，根据编码打印对应的终结符或非终结符
    for (int i = 0; i <= charTop; ++i) {
        char c = (charStack.data[i] <= numVT) ? VT[charStack.data[i]] : VN[charStack.data[i] - OFFSET];
        cout << c << " ";
    }
    // 打印空格，使符号栈和输入串对齐
    for (int i = 2 * charTop; i < 29; ++i) cout << " ";
    //输入串
    for (int i = ip; i < str.size(); ++i) {
        cout << str[i];
    }
    for (int i = 0; i < 20 - str.size() + ip; i++) cout << " ";

}