Dijkstra 算法的简易推导及练习

图的基本概念及术语

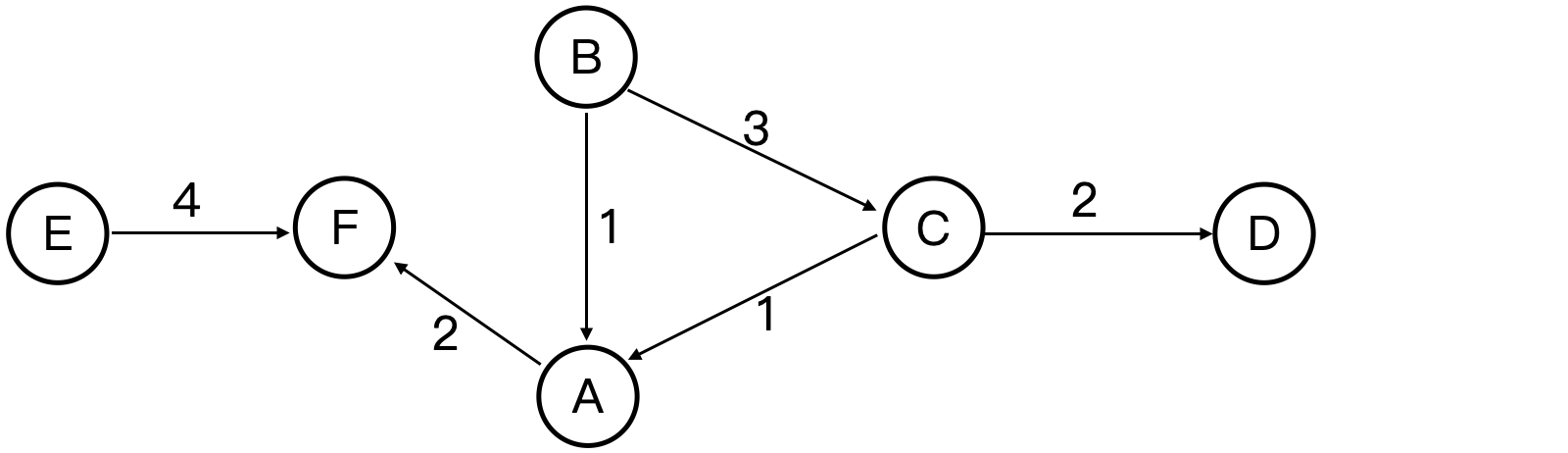
读者可能不熟悉图论基础知识的一些符号，特此解释一部分。

突然接收这么多知识确实有些挑战，跟着学术一点的图论教程逐步学到这里会好很多，具体可参考《图论入门》。

• $G$：图
• $V$: 点集, 在上图中， V = { a , b , c , d , e , f } V = \{a,b,c,d,e,f\} V={a,b,c,d,e,f}
• $E$：边集
• $w$: 权重函数，上图中边上的数字，比如 $w(c,a)=1$。读者如果不熟悉图理解为边的长度即可。
• $\forall$: 任意
• $(u,v)$: 从点 $u$ 到点 $v$ 的边，一般表示能从 $u$ 走向 $v$。
• $\in$: 属于

所以 $\forall (u,v)\in E,w(u,v)\ge 0$ 表示边集中任意边的权重 $\ge 0$。

其他的相关符号还有：

• $|V|$ 或者 $|G.V|$表示集合 $V$ 的 size
• $\delta (u,v)$ 表示图中 $u,v$ 两点的距离（最短路径的权重和）。
• V δ ∪ { e } V_\delta \cup \{e\} Vδ​∪{e} 表示向点集 $V_{\delta }$ 中加入点 $e$。
• $G.Adj$ 表示邻接表, 上图中 G . A d j [ c ] = { a , d } G.Adj[c] = \{a,d\} G.Adj[c]={a,d}。存储从各点出发的可直达点以及权重，但在学术中权重用权重函数 𝑤 来表达。

最短路径

最短路径 (shortest paths) 的相关实际场景比较广泛，比如地图、网络等。

单源最短路径 (SSSP / single-source shortest paths) 是求解给定某一源点到其所有可达点的最短路径，即使得这些无权路径的边数或者带权路径的权重和最小。

Dijkstra 算法解决的是非负权图的 SSSP，未使用堆查找优化时，也被称为 Dijkstra 暴力算法。

Dijkstra 发音 /ˈdaɪkstrə/，译作“迪杰斯特拉“。

松弛 (Relax)

"松弛"这个术语出现得较多，含义同数学意义上的松弛相同，减少声明成立的约束条件。图的两点之间存在多条路径，找到最短的一条需要比较，每比较一次就减少一次约束。

但我认为此处从数学中沿用这个命名并不好。

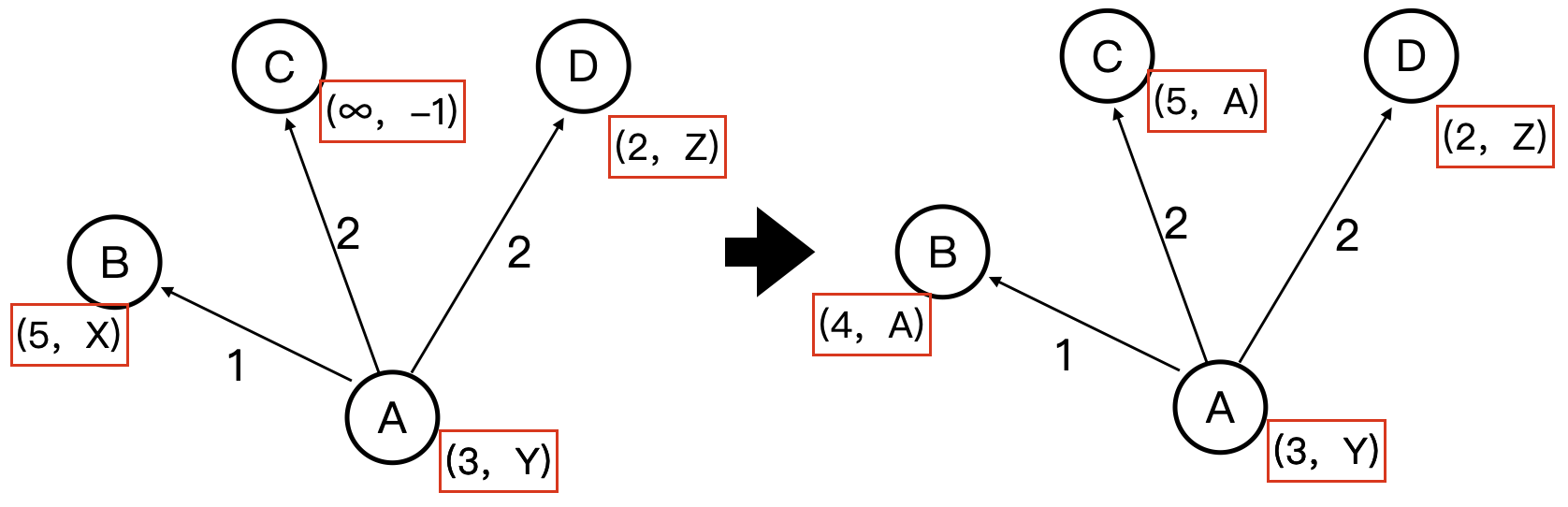
上图表示在 SSSP 中，忽略原图中的其他点和边，探索过程中某一时刻点 A 对其邻接点的松弛。

红框中的下标：

• 第一个：在当前探索范围内，源点到该点的的距离。

• 第二个：相应路径上的父节点。和各顶点一样，都是实际以数字存储，-1 表示没有父节点。

观察 A B 两点状态，3 + 1 < 5，说明 A 点所处路径向 B 延伸后比此前源点到 B 的路径更短，松弛有效。
同理可得对 C 松弛有效，对 D 松弛无效。
如果之后某刻 A 点再次被有效松弛了，那么应该继续松弛 B C D 点。

原理

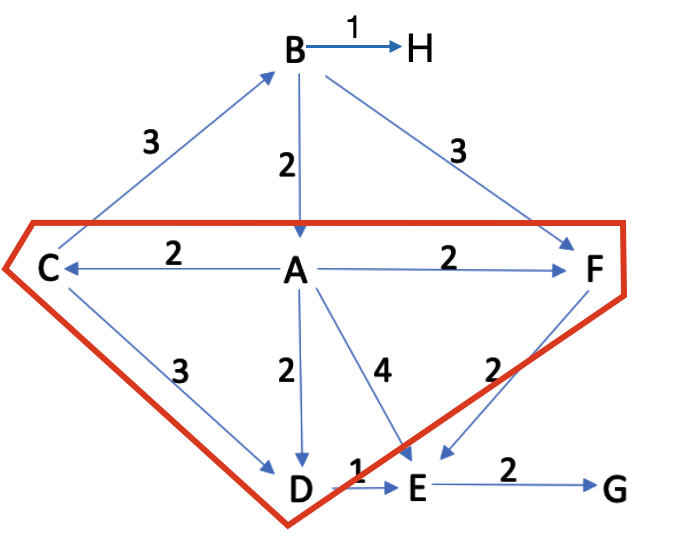
如上图所示，给定图 $G=(V,E,w)，\forall (u,v)\in E,w(u,v)\ge 0$。$a$ 为源点，求其到各可达点的最短路径。
设红框区域中的点集为 $V_{\delta }$，表示 $V$ 中前 $|V_{\delta }|$ 个从 $a$ 出发最近的点。
记某时刻 V δ = { a , c , d , f } V_{\delta} = \{a, c, d, f\} Vδ​={a,c,d,f}。这与 Prim 算法很相似。

从 $V_{\delta }$ 外的可直达点 $b,e$ 中选择离 $a$ 最近的 $e$ 点，记录相应路径 $⟨a,d,e⟩$ 和其长度。
从 $V_{\delta }$ 外的不可直达点 $h,g$ 中任选一点记为 $v^{⇝}$，路径 $a⇝v^{⇝}$ 上一定至少经过 $b$ 或 $e$，记该点为 v → ∈ { b , e } v^\rightarrow \in \{b, e\} v→∈{b,e}，路径为 $a⇝v^{\to }⇝v^{⇝}$。
既然 $\forall (u,v)\in E,w(u,v)\ge 0$，则 $\delta (a,v^{\to })\le \delta (a,v^{⇝})$
根据 $e$ 点的选择条件可知 $\delta (a,e)\le \delta (a,v^{\to })$，结合上式可得 $\delta (a,e)\le \delta (a,v^{⇝})$
所以 $e$ 为 { b , e , h , g } \{b,e,h,g\} {b,e,h,g} 即 $V-V_{\delta }$ 中离 $a$ 最近的点，此前记录的 $⟨a,d,e⟩$ 为最短路径。

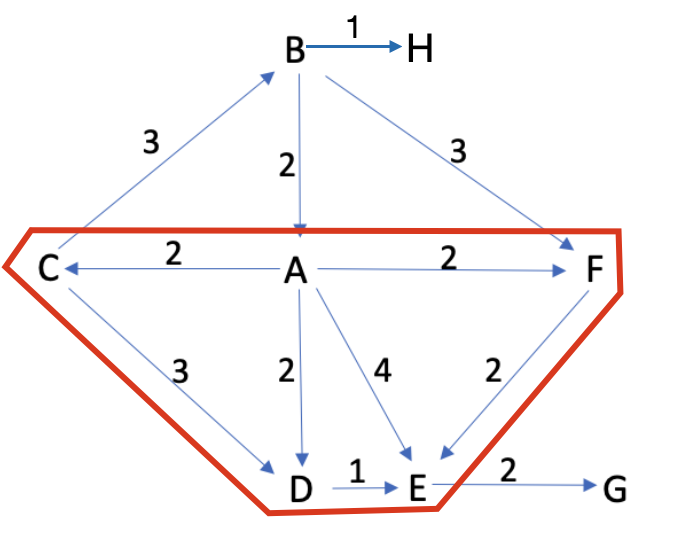
如上所示，令 V δ = V δ ∪ { e } V_\delta = V_\delta \cup \{e\} Vδ​=Vδ​∪{e}。再执行上一步，逐渐扩张即可找到 $a$ 到所有可达点的最短路径。

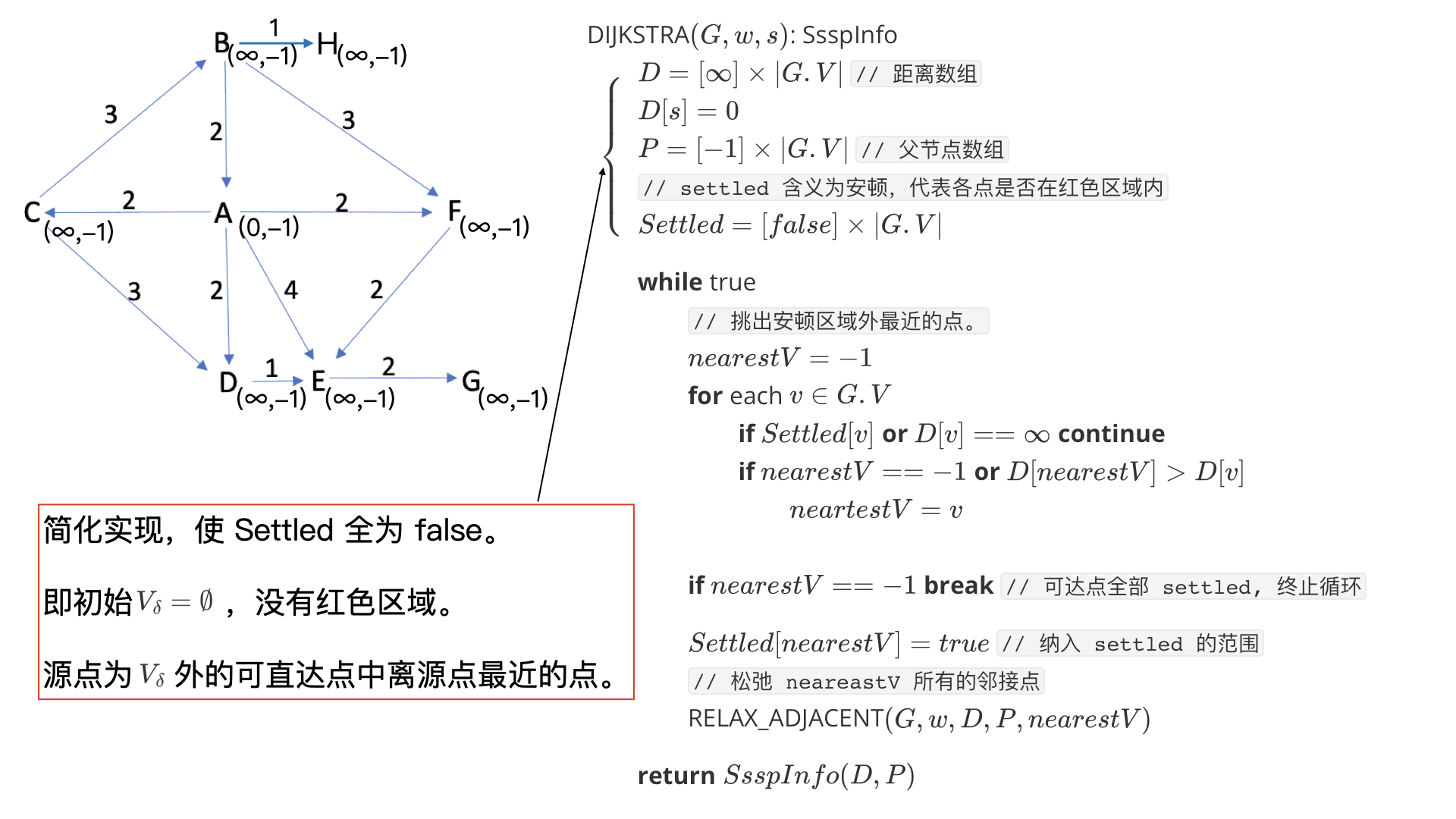
初始 V δ = { a } V_\delta = \{a\} Vδ​={a}

Dijkstra 算法和 Prim 算法相比，取得周围最近点的思路有所变化，详见下面的算法实现。

求解

$[-1]\times |G.V|$ 表示长度为 $|G.V|$，元素都为 $-1$ 的数组。
读者在初次接触伪代码时会不习惯。但据笔者的调查反馈，习惯后体验还是不错的。具体的术语和符号均在《图论入门》的附录中有介绍。

松弛部分被我抽离为一个函数，此函数表示松弛点 $u$ 的所有邻接点。

• $D$ 为数组 Distances，表示在当前探索范围内，源点到各点的距离。
• $P$ 为数组 Parents，表示相应路径上的父节点。
• $D$ 和 $P$ 的数组下标表示顶点。

-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-

-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=--=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
记源点只通过已知的 $V_{\delta }$ 到周围可直达点的最短距离和路径为 $f(V_{\delta })$。

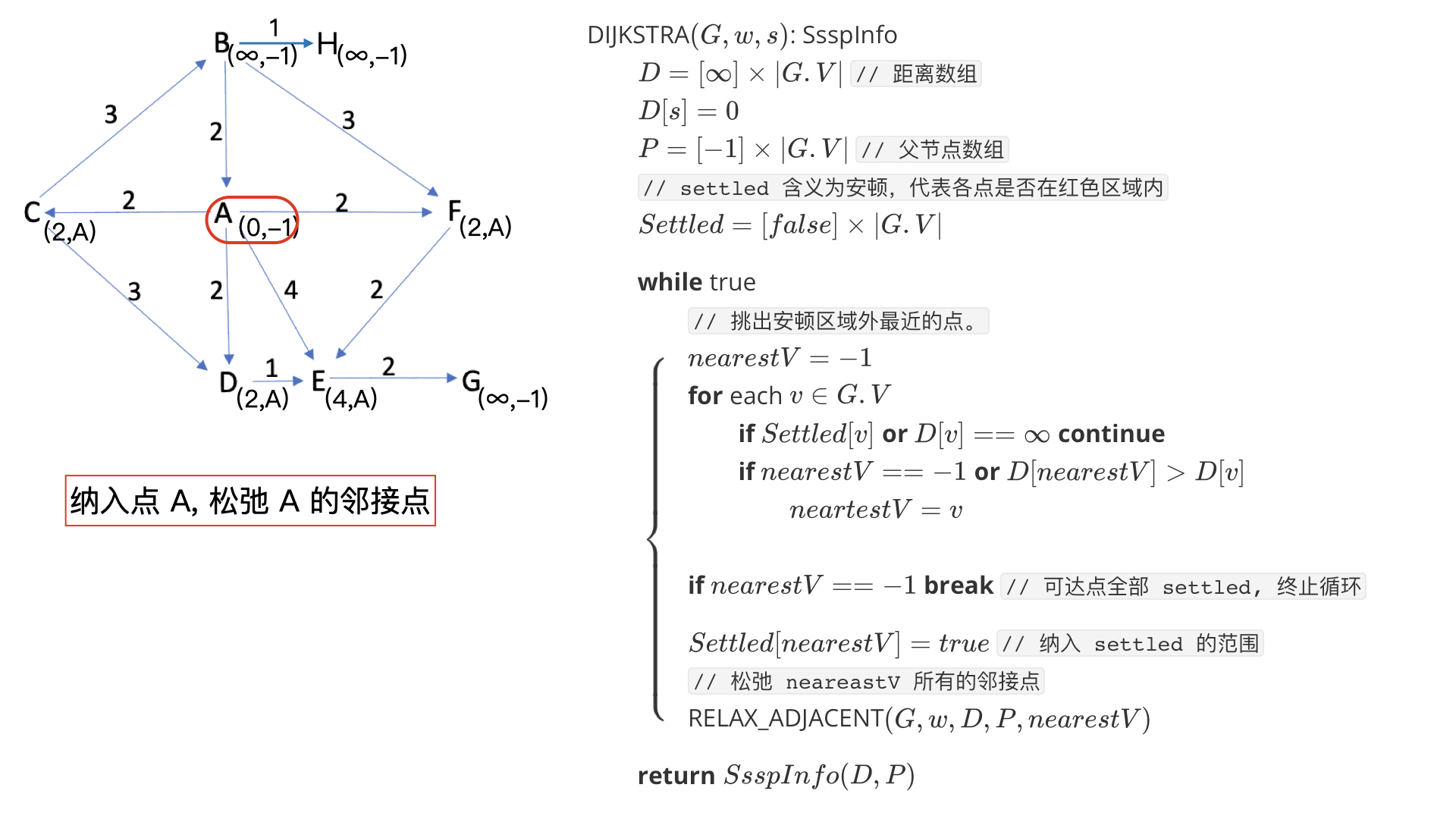
可得如果某一次松弛前，我们已经确定了 $V_{\delta }$ 和 $f(V_{\delta })$，那么我们根据以上证明取最近的一点纳入 $V_{\delta }$ 是没错的，而且松弛该点的邻接点后就可以更新 $f(V_{\delta })$。

完整代码

思考为什么松弛前不用判断点 $nearestV$ 的邻接点是否 settled?

答：因为处于 settled 的点已经找到最短距离，松弛会一直无效。

除 Settled 外还有一些常见的命名，如 Visited、Done、Used。从语义上来看，Settled 和 Done 更加合适一些。

在很多只考虑距离的应试题中，$D[v]$ 的更新可以简写为 $D[v]=min(D[v],D[nearestV]+w(nearestV,v))$。

复杂度

时间：$O(V^2)$
空间：$\Theta (V)$

与 Prim 算法的复杂度分析大体相同，但本章考虑不可达导致提前截止的情况，所以时间复杂度不是 $\Theta (V^2)$。还可以用堆查找优化，但实现稍复杂，这在《图论进阶》中有讲到。

练习

给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例1:

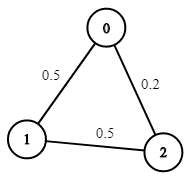
输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2

输出：0.25000

解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

求解：

Dijkstra 算法中的权重累计方式是相加，秉承非递减原则，最短路径上的权重和最小。

本题的权重累计方式是相乘，但权重(概率) $\in [0,1]$，秉承非递增原则，求解概率最大的路径。

所以可以镜像转换松弛过程，代码如下所示。

根据原题中的提示部分（未展示在这里），可知该图是稀疏图，所以主流解法是二叉堆查找优化的版本。但这不属于内地本科的教学范围，在面试中也经常不太苛刻。二叉堆查找优化正好也属于《图论进阶》中免费的试读部分，读者有兴趣可以结合《图论入门》中 Prim 算法的两种堆查找优化看一下。

以下均为个人所著，兼顾了面试、本科、硕士阶段，包含清晰的 PPT 动画展示以及配套的练习题。读者也在陆续写其他算法教程。

• 附个人题解的双指针题单

• 图论入门

• 图论进阶