多臂老虎机问题

多臂老虎机问题

问题简介

每次在多个动作(选项–老虎机)中选择一个,只考虑一个状态(即选择玩每个老虎机所得到的奖励不随时间变化),每次选择后获得一个随机分布(此随机分布取决于你的动作)的奖励(这里定义为真实奖励加一个高斯扰动).你的目标是在一定时间步内使(真实)收益最大化.

注意:步步最优非全局最优,我们要平衡"explore"和"exploit"的问题,即"步步最优非全局最优".

动作价值方法

首先定义几个变量:
1.动作$a=0,1,2,...,n-1$, 其中$n$代表老虎机数量;
2.每个动作的价值$q(a)$
3.每个时间步下每个动作的价值$R_t(a)$,$t$代表时间.
3.每个时间步下的动作评价函数$Q_t(a)$
由大数定律,我们可以直接定义$Q_t$如下:
$$Q_t(a)=\frac{{\sum }_i^{N_t(a)}{R}_i}{N_t(a)}$$
其中$N_t(a)$代表在时间t之前动作a被选择的次数,每个$R_i$则是记录过的关于选择过a所获得的价值.由于$$R_i(a)=q(a)+ϵ,ϵ-N(0,1)$$则容易知道$$Q_t(a)\to q(a),N_t(a)\to +\infty$$.这样我们便可以选出最优的那个动作(老虎机).我们由greedy算法和$ϵ$-greedy算法.

greedy算法: 每步都选择动作$a=argma{x}_a{R}_t(a)$,由于噪声的存在以及初始选择的不确定性不一定能在有限时间内选择到最好的动作;

$ϵ$-greedy算法: 每步有$1-ϵ$的概率执行greedy算法操作, $ϵ$的概率从动作中随机选择一个.此方法能保证每个动作都被选择到,确保收敛.

代码如下:

'''an algorithmn about n-armed bandit  
introduction
n -- number of slot machine
q(a) -- scores about each action, obeying the gauss distribution with the mean of 0 and varience of 1. 
        the action is which machine you choose, from 1 to n(or 0 to n-1)


'''
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)
n = 10
T = 10000
tspan = np.arange(T)
eps = 0
q = np.random.normal(0,1,n)

class ArmedBandit:
    def __init__(self, n,  q) -> None:
        self.n = n
        self.q = q
        self.Actions = np.arange(n)
    def Action(self, t, eps):
        exploration_flag = True if np.random.uniform() <= eps else False
        noise = np.random.normal(0,1,self.n)
        repay = q + noise
        if exploration_flag:
            a = np.random.randint(self.n)
        else: 
            Q = []
            for i in range(n):
                Q.append((sum(self.Repay_list[i]) + repay[i]) / len(self.Repay_list[i]))
            a = np.argmax(np.array(Q))
        self.Repay_list[a].append(repay[a])
        avg = (q[a] + self.Reward_avg[-1] * t) / (t + 1)
        self.Reward_avg.append(avg)
        return a
    def play(self, T, eps):
        self.ActionRecord = []
        self.Repay_list = [[0] for _ in range(n)]
        self.Reward_avg = [0]
        for t in range(T):
            a = self.Action(t, eps)
            self.ActionRecord.append(a)
        return self.ActionRecord, self.Reward_avg[:-1]

if __name__ == "__main__":
    slot_machine = ArmedBandit(n, q)
    actions, reward_avg=  slot_machine.play(T, eps=0)
    actions1, reward_avg1 = slot_machine.play(T, eps=0.01)
    actions2, reward_avg2 = slot_machine.play(T, eps=0.1)
    plt.figure()
    plt.plot(tspan, reward_avg, label='eps=0')
    plt.plot(tspan, reward_avg1, label='eps=0.01')
    plt.plot(tspan, reward_avg2, label='eps=0.1')
    plt.xlabel('Steps')
    plt.ylabel("Average reward")
    plt.title("n Armed Bandit")
    plt.legend()
    print(actions2)
    plt.show()

结果如下:

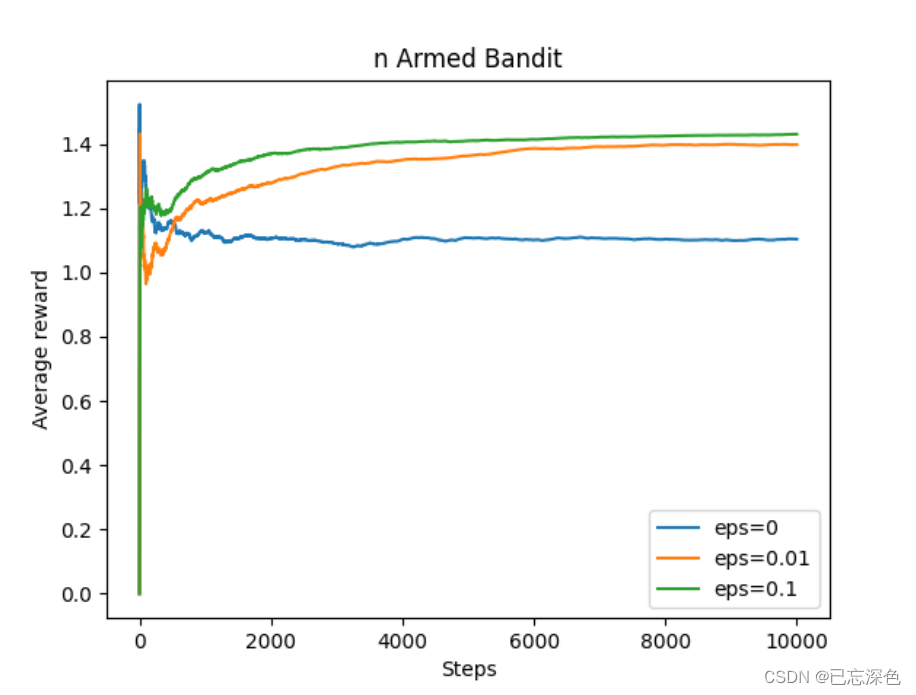
可见在学习过程中,适当的"explore"是有必要的.

简化实现

我们可以利用上述思想实现,但及其消耗计算和存储资源(每次都要存储一个$R_t$, 每次都要计算所有的$R_t$相加以比较).为此,我们简化公式:
$$\begin{array}{rl}{Q}_{k+1}& =\frac{1}{k}\sum _{i=1}^k{R}_k\\ & =\frac{1}{k}(R_k+(k-1)Q_k)\\ & =Q_k+\frac{1}{k}(R_k-Q_k)\end{array}$$
这样,我们每次只需要存储$Q_k,R_k$了,极大节省资源.且我们推出一个在强化学习中的一个重要公式:
$$NewEstimate\leftarrow OldEstimate+StepSize(Target-OldEstimate)$$
这里我们的$step=1/k$.

在处理单状态任务(如此任务时)此步长满足大数定律,是合乎逻辑的,但当处理状态改变情形时,步长的选择更加复杂.

此外,初始动作评估函数的设置对"expolre"或是"exploit"有影响.如果初始评估函数设置较大,开始获得的动作价值函数吸引力不够大,从而增强一定时间的"explore".

参考:
多臂老虎机入门
Reinforcement Learning: An Introduction