vLLM学习笔记-FlashAttention-更新ing

Ref：

理论：

1. Flash Attention学习过程【详】解（已完成！）_哔哩哔哩_bilibili
2. 神经网络量化与部署
3. Flash Attention 为什么那么快？
4. 关于KVCache
5. 关于CUDA版本实现
6. 论文
7. 知乎
8. 关于Transformer
9. 关于3Pass-OnlineSoftmax

面经：

1. 鹅厂
2. 面试连环炮

OnlineSoftmax

我把知乎的知识点进行了简单总结：

注意：

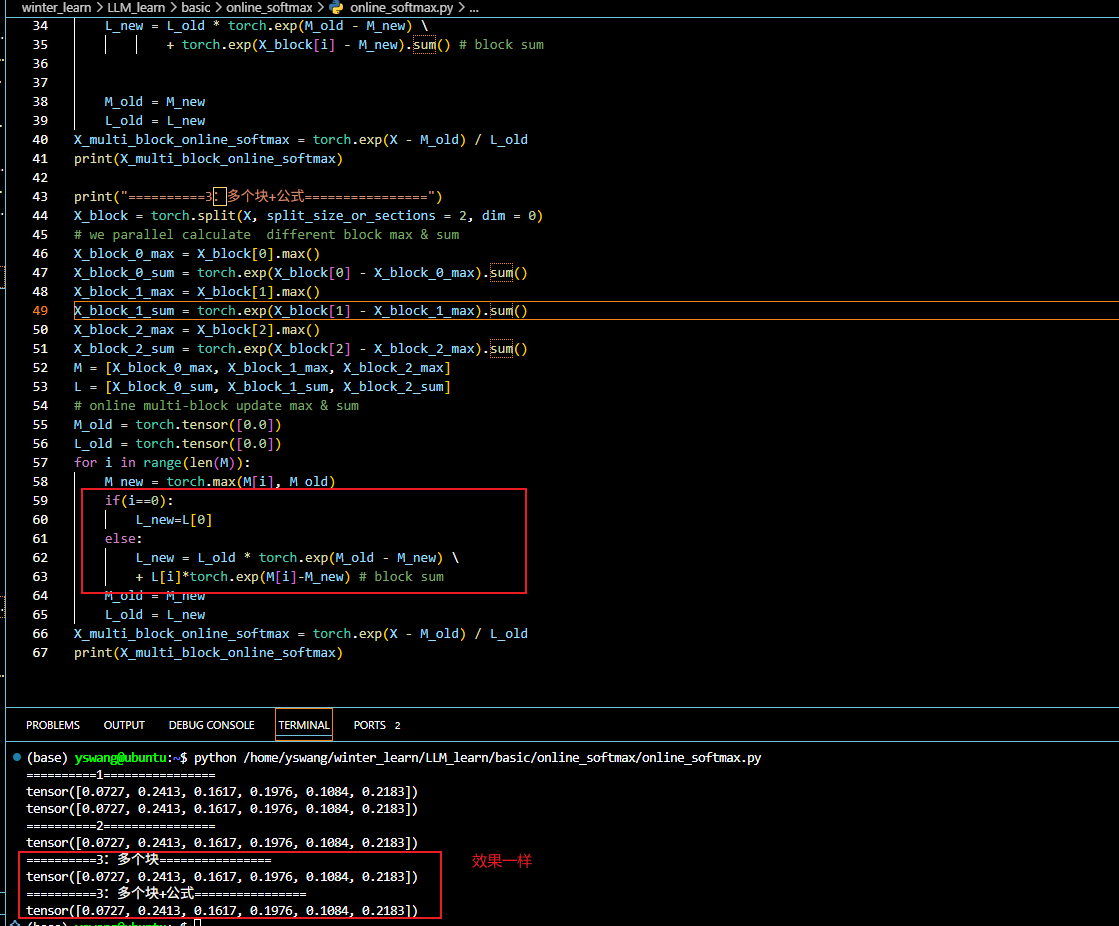
3个块的OnlineSoftmax的处理上，作者进行了一个顺便的推导和优化，我这里用原公式结果是一样的。

代码手撕

前文的学习代码实现如下：

import torch
print("==========1================")
X = torch.tensor([-0.3, 0.9, 0.5, 0.7, 0.1, 0.8])
X_sum_exp=X.exp().sum()
X_exp=X.exp()
X_exp1=torch.exp(X)
X_head=X_exp/X_sum_exp
X_head1=X_exp1/X_sum_exp
print(X_head1)
# print(X_exp)
# print(X_exp1)
print(X_head)
print("==========2================")
X_max=X.max()
X_sub=X-X_max
X_head_sub=torch.exp(X_sub)/torch.exp(X_sub).sum()
print(X_head_sub)
print("==========3：多个块================")
X_block = torch.split(X, split_size_or_sections = 2, dim = 0) 
# we parallel calculate  different block max & sum
X_block_0_max = X_block[0].max()
X_block_0_sum = torch.exp(X_block[0] - X_block_0_max).sum()
X_block_1_max = X_block[1].max()
X_block_1_sum = torch.exp(X_block[1] - X_block_1_max).sum()
X_block_2_max = X_block[2].max()
X_block_2_sum = torch.exp(X_block[2] - X_block_2_max).sum()
M = [X_block_0_max, X_block_1_max, X_block_2_max]
L = [X_block_0_sum, X_block_1_sum, X_block_2_sum]
# online multi-block update max & sum
M_old = torch.tensor([0.0])
L_old = torch.tensor([0.0])
for i in range(len(M)):
    M_new = torch.max(M[i], M_old) 
    L_new = L_old * torch.exp(M_old - M_new) \
            + torch.exp(X_block[i] - M_new).sum() # block sum，因为这个是一个block的
    

    M_old = M_new
    L_old = L_new
X_multi_block_online_softmax = torch.exp(X - M_old) / L_old
print(X_multi_block_online_softmax)

print("==========3：多个块+公式================")
X_block = torch.split(X, split_size_or_sections = 2, dim = 0) 
# we parallel calculate  different block max & sum
X_block_0_max = X_block[0].max()
X_block_0_sum = torch.exp(X_block[0] - X_block_0_max).sum()
X_block_1_max = X_block[1].max()
X_block_1_sum = torch.exp(X_block[1] - X_block_1_max).sum()
X_block_2_max = X_block[2].max()
X_block_2_sum = torch.exp(X_block[2] - X_block_2_max).sum()
M = [X_block_0_max, X_block_1_max, X_block_2_max]
L = [X_block_0_sum, X_block_1_sum, X_block_2_sum]
# online multi-block update max & sum
M_old = torch.tensor([-1000.0])
L_old = torch.tensor([0.0])
for i in range(len(M)):
    M_new = torch.max(M[i], M_old) 
    if(i==0):
        L_new=L[0]
    else:
        L_new = L_old * torch.exp(M_old - M_new) \
        + L[i]*torch.exp(M[i]-M_new) # block sum
    #比完后就成旧的了
    M_old = M_new 
    L_old = L_new
X_multi_block_online_softmax = torch.exp(X - M_old) / L_old
print(X_multi_block_online_softmax)

print("==========4：2Pass-Online================")
M_old = torch.tensor([-1000.0])
L_old = torch.tensor([0.0])
O=torch.zeros(len(X))
for i in range(len(X)):
    M_new=torch.max(X[i],M_old)
    L_new=L_old*torch.exp(M_old-M_new)+torch.exp(X[i]-M_new)#不需要sum，因为就一个 
    M_old=M_new
    L_old=L_new
for i in range(len(X)):
    O[i]=torch.exp(X[i]-M_new)/L_new

# 用O=torch.exp(X-M_old)/L_old也行

print(O)

FlashAttention

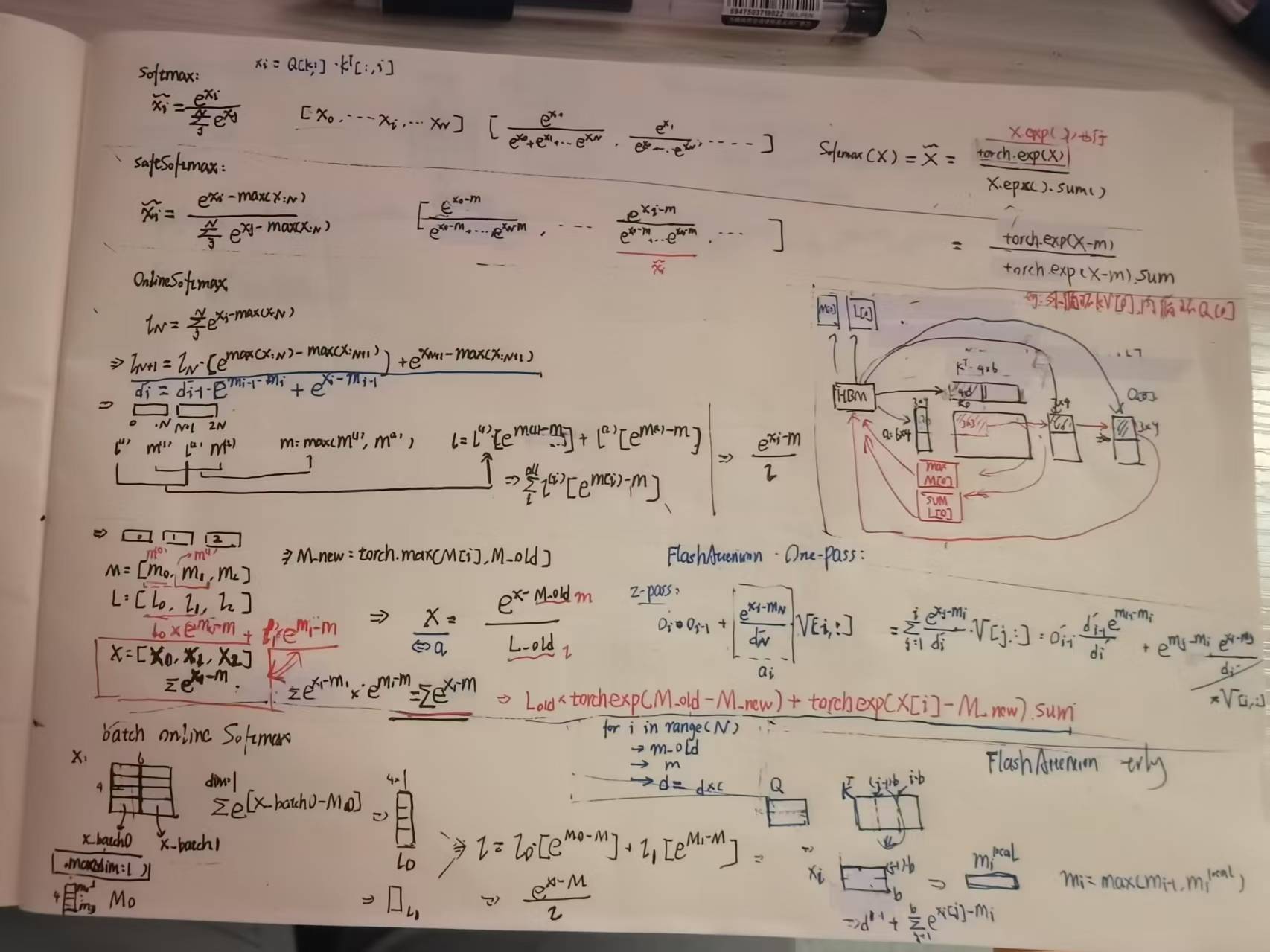
对照前面的OnlineMax和batch形式的SoftMax可以很容易推导出One-Pass形式的FlashAttention以及tiling形式的FlashAttention。基于上，便可以理解HBM和SRAM中KVCache是如何交换的了。

注意蓝笔部分，d即为之前的l，也即三个循环。基于这个可以推导出o也就是One-Pass的FlashAttention。

内存访问优化

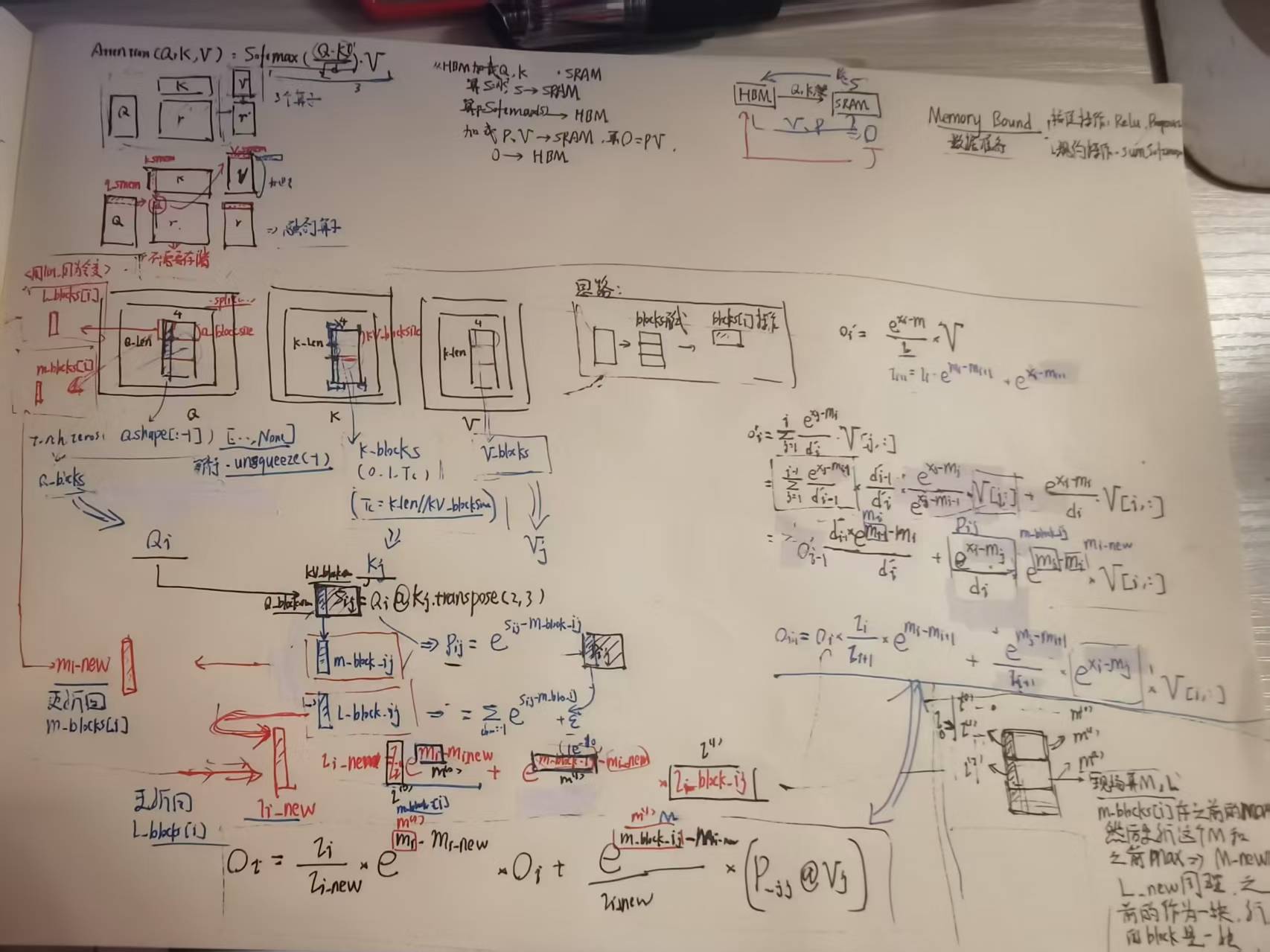
如上，访存优化主要是针对Memory Bound。

CPU版本的FlashAttention实现可以算出$Q{K}^T$也就相当于之前的X了，然后可以算出OnlineSoftMax然后和V计算。

不过之前推导了One-Pass形式，所以也可以用那个公式。

代码手撕

给出FlashAttention的CPU版本代码手撕

import torch
INF=-1e10
EPSILON=1e-8
Q_len=6
KV_len=8
Q_block_size=3
KV_block_size=2
Q=torch.randn(1,1,Q_len,4,requires_grad=True).to(device='cpu')
K=torch.randn(1,1,KV_len,4,requires_grad=True).to(device='cpu')
V=torch.randn(1,1,KV_len,4,requires_grad=True).to(device='cpu')
Tc=KV_len//KV_block_size
Tr=Q_len//Q_block_size
m=torch.ones(Q.shape[:-1])[...,None]*INF
l=torch.zeros(Q.shape[:-1])[...,None]
m_blocks=list(m.split(split_size=Q_block_size, dim=2))
l_blocks=list(l.split(split_size=Q_block_size, dim=2))
O=torch.zeros_like(Q,requires_grad=True)
Q_blocks=Q.split(split_size=Q_block_size, dim=2)
K_blocks=K.split(split_size=KV_block_size, dim=2)
V_blocks=V.split(split_size=KV_block_size, dim=2)
O_blocks=list(O.split(split_size=Q_block_size, dim=2))

for j in range(Tc):
    K_j=K_blocks[j]
    V_j=V_blocks[j]
    for i in range(Tr):
        Q_i=Q_blocks[i]
        X=Q_i @ K_j.transpose(-2,-1)
      
        M=X.max(dim=-1, keepdim=True).values
        L=torch.exp(X-M).sum(dim=-1, keepdim=True)+EPSILON
        P=torch.exp(X-M)

        M_new= torch.maximum(m_blocks[i], M)
        L_new=L*torch.exp(M-M_new)+torch.exp(m_blocks[i]-M_new)*l_blocks[i]
        

        O_blocks[i]=(l_blocks[i]/L_new)*torch.exp(m_blocks[i]-M_new)*O_blocks[i] + torch.exp(M-M_new)/L_new*(P@V_j)
        m_blocks[i]=M_new
        l_blocks[i]=L_new
        print(f'-----------Attn : Q{i}xK{j}---------')
#         print(O_BLOCKS[i].shape)
        print(O_blocks[0])
        print(O_blocks[1])
        print('\n')

print('-----------------Final O-----------------')
O=torch.cat(O_blocks, dim=2)

print(O)

print('-----------------Final O-----------------')
O = torch.softmax ( Q @ K.transpose(2,3), dim = -1) @ V
print(O)

面经

按 softmax 公式的计算有什么问题，在工程实现的时候怎么做的？

• 数值溢出->SafeSoftmax

你能够降低 softmax 的 GPU 访存复杂度吗？

• 第一，你知不知道 softmax 可以通过流式计算降低 GPU 访存复杂度。
• 第二，能否阐述一下流式计算的核心思想。

softmax 能做到流式计算，核心思想就是把 softmax 分母的计算做了一个优化，让它不依赖全局的最大值 $m_N$，而是依赖局部的最大值$m_i$，这样就把前两个步骤合并成了一个。

所以最终我们可以借助 GPU 的 share memory 来存储中间结果，将上面的两步只用一个 kernel 实现，这样就只需要与 global memory 通信两次，一次写入数据，一次读取结果。

不过这里要注意，就是由于第二步的计算仍然需要依赖第一步计算的分母 $d_N$，所以还是需要两步，换句话说，不能做成 one pass。

既然 softmax 不能做到 one-pass，为什么 Flash Attention 可以，解释一下背后的核心思想？

• 核心思想是 Flash Attention 让 Attention 的所有计算都符合加法结合律，这样就可以充分利用 GPU 的并行优势，这是面试官希望我们答出的第一个点。
  

详细解释一下 Flash Attention 中的 tiling 策略？

• 知不知道什么是 tiling，为什么要使用它？以及使用之后有什么作用？其次在 Flash Attention 中的 tiling 策略是如何做的，能否说一下它的整个流程以及具体的效果？

FlashAttention 对 MQA 和 GQA 是怎么处理的？

• 一个关键词，就是 Indexing 思想。对于 MQA 和 GQA，FlashAttention 采用了 Indexing 的方式，而不是直接复制多份 KV Head 的内容到显存然后再进行计算。
  
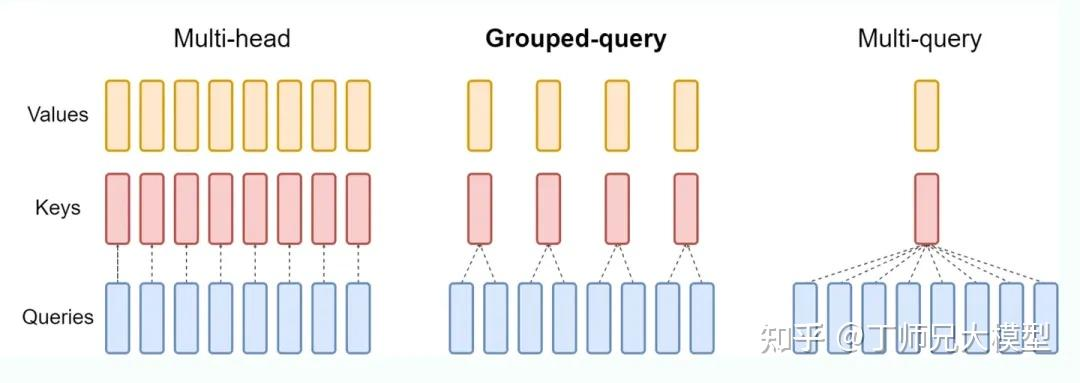
  Indexing 的思想，就是通过传入 KV Head 索引到 GPU Kernel 中，然后根据内存地址，直接从内存中读取 KV。

vllm-FlashAttention源码

FlashAttentionBackend

class FlashAttentionBackend(AttentionBackend):

获取head_sizes等属性，继承自AttentionBackend作为后端。
注意：类似-> Type["FlashAttentionImpl"]的用法。
注意：

    @staticmethod
    def swap_blocks(
        src_kv_cache: torch.Tensor,
        dst_kv_cache: torch.Tensor,
        src_to_dst: torch.Tensor,
    ) -> None:
        src_key_cache = src_kv_cache[0]
        dst_key_cache = dst_kv_cache[0]
        ops.swap_blocks(src_key_cache, dst_key_cache, src_to_dst)
        src_value_cache = src_kv_cache[1]
        dst_value_cache = dst_kv_cache[1]
        ops.swap_blocks(src_value_cache, dst_value_cache, src_to_dst)

用于交换KVCache中特定块。为什么这样做？（分别交换键缓存和值缓存？）

FlashAttentionMetadata

@dataclass
class FlashAttentionMetadata(AttentionMetadata):

其中：

seq_lens: Optional[List[int]]           # 每个序列的总长度（列表形式）
seq_lens_tensor: Optional[torch.Tensor]  # 序列长度的张量表示
max_prefill_seq_len: int                 # 预填充阶段的最大序列长度
max_decode_seq_len: int                  # 生成阶段的最大序列长度
context_lens_tensor: Optional[torch.Tensor]  # 已计算的上下文长度（张量）

​