本篇将分享关于点积与对偶性相关内容
点积与对偶性
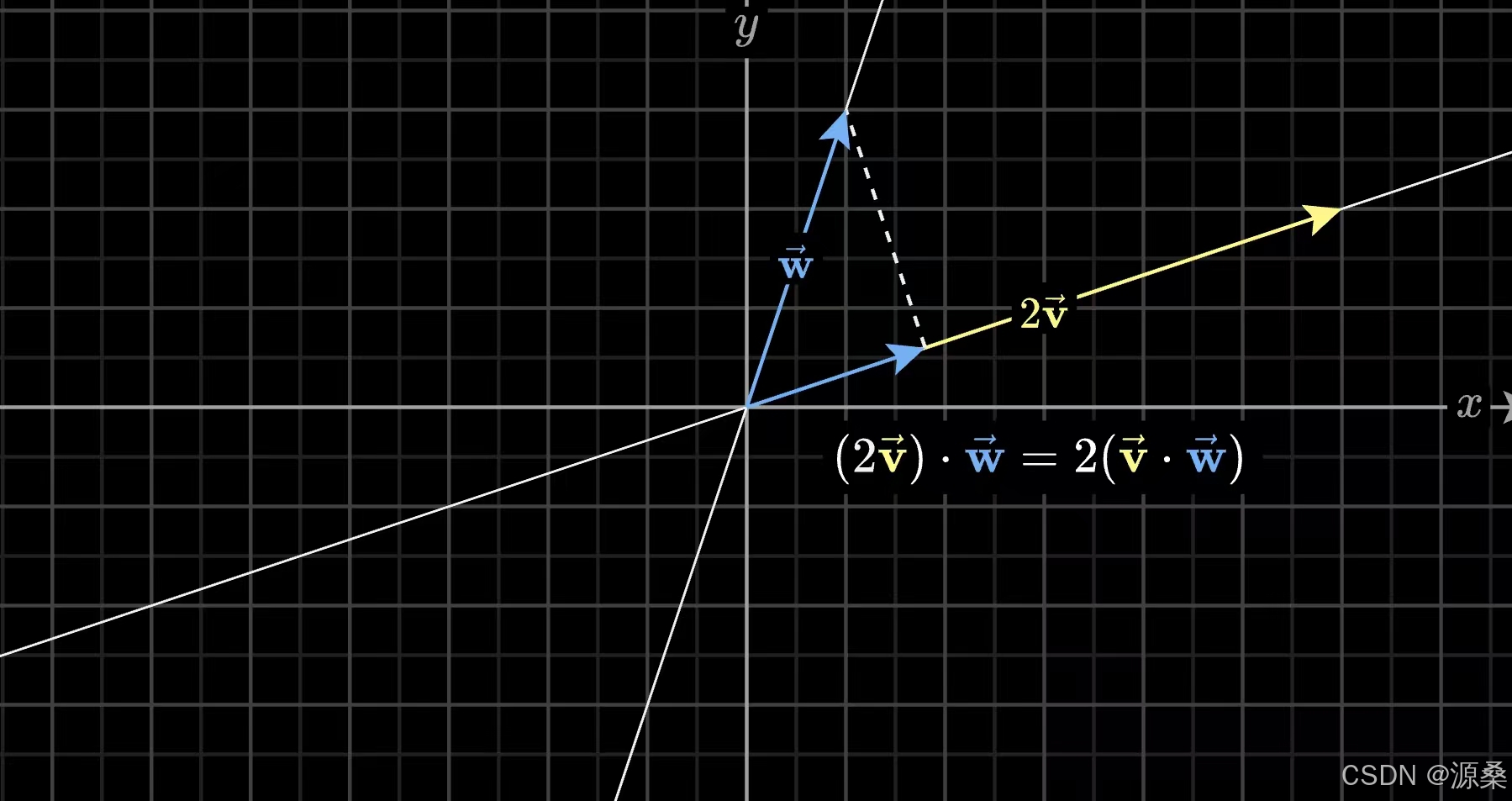
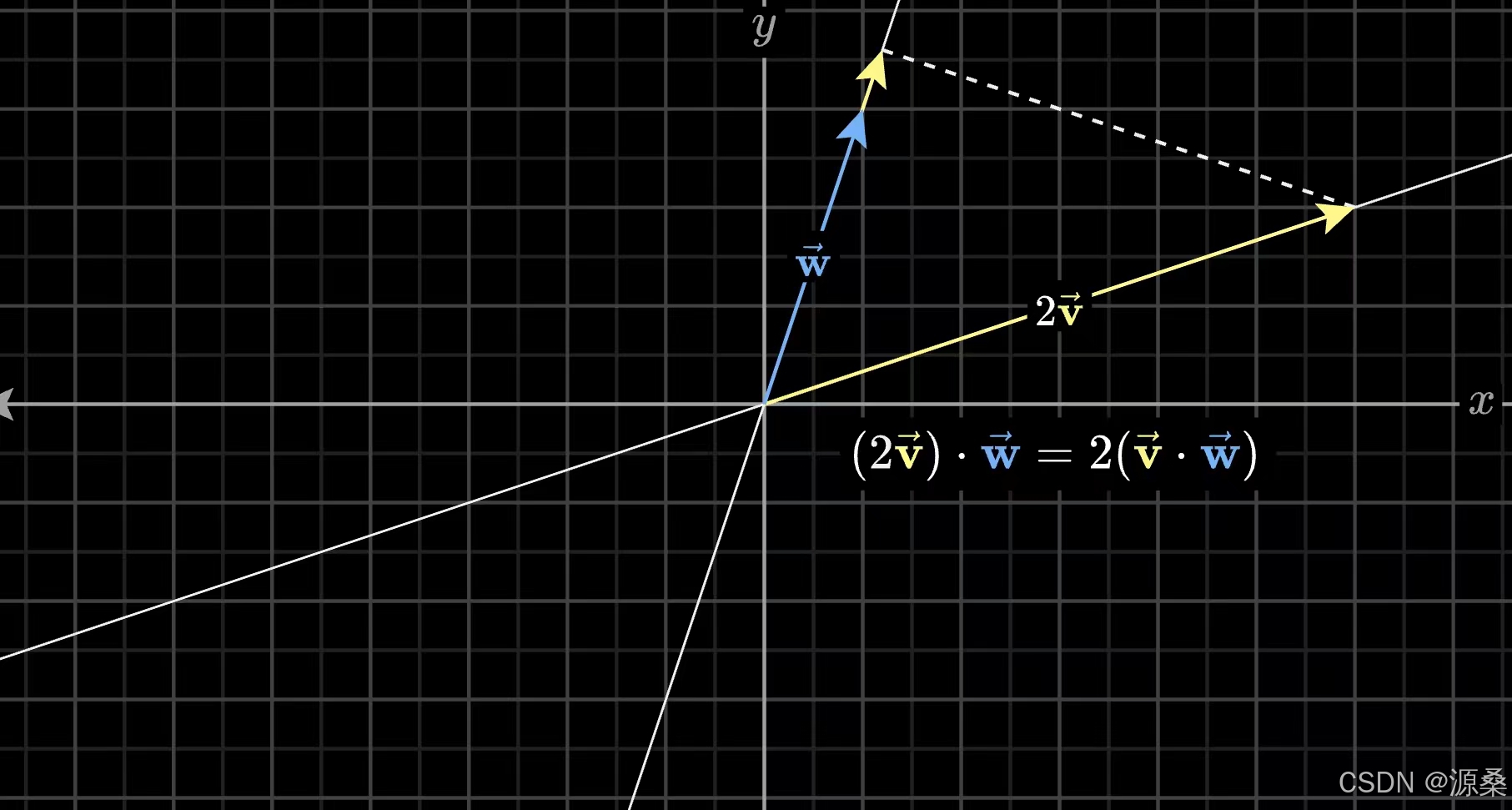
向量点积的计算过程是将向量对应坐标相乘再相加,这个过程在几何上的解释是:一个向量在另一个向量上投影,将投影的长度乘以另一个向量的长度。通过点积的正负可以很容易判断两个向量的方向是否大致相同,又或者通过是否为零判断向量垂直。这里有一点性质可能会使初学者有些迷惑:无论哪个向量向另一个向量投影,最后计算的值是相同的。我们先从两个长度相同的向量v、w举例,由对称性很容易证明这个性质,这时我们将向量v的长度变为原来的2倍,将w投影到v上,它们的点积写作,因为v的长度不影响w投影的长度,因此
应该等于
。然后换个方式投影,将2v投影到w上,此时投影长度变为了原来的2倍,从数值上来看它依然是
的两倍。因此点积的结果与投影方式无关。
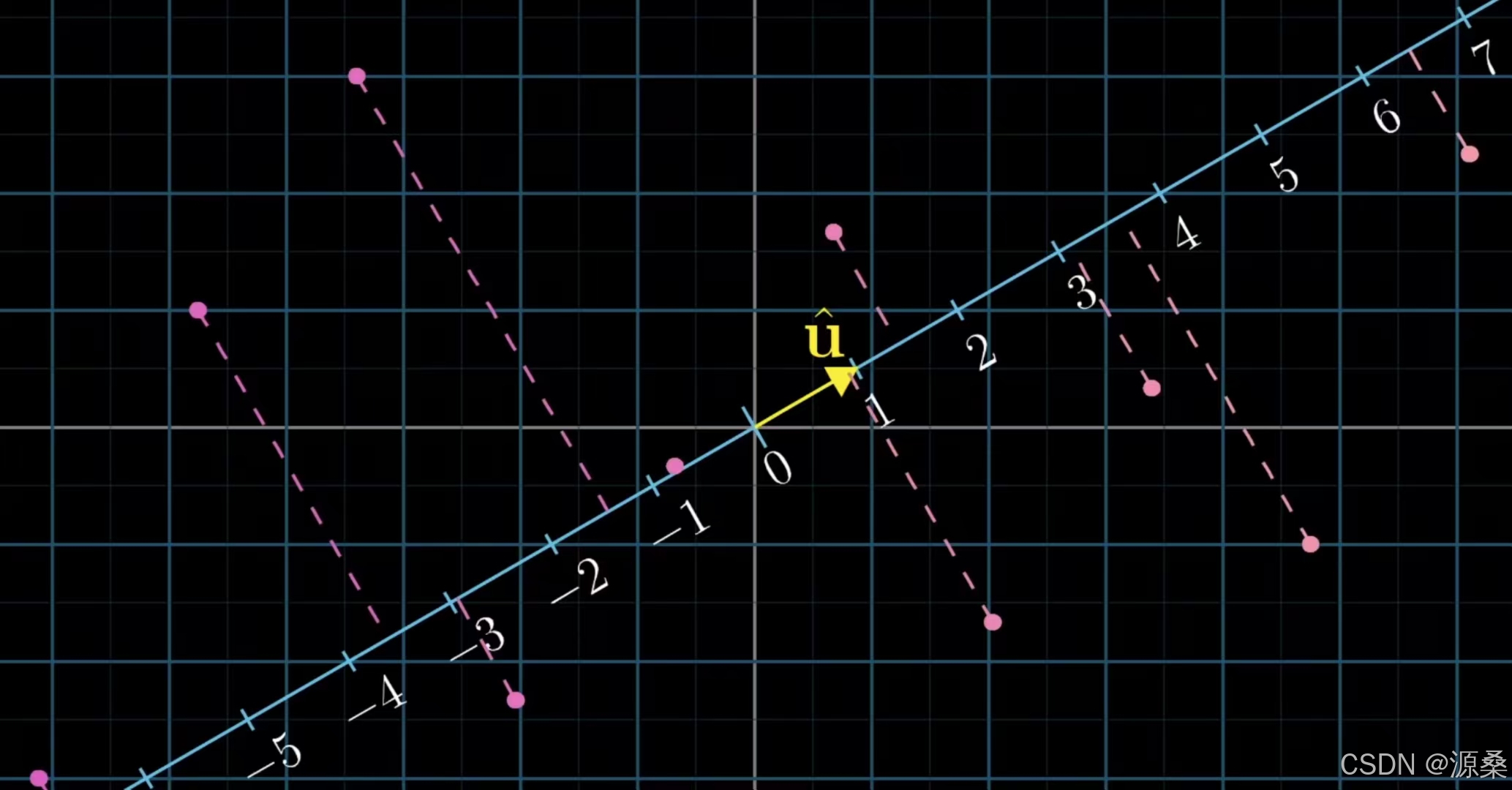
你有没有想过为什么点积要与投影联系在一起呢,接下来就由对偶性来解答点积的本质。首先我们想象二维平面中存在一个过原点斜着放的数轴,这时有一种线性变换使得平面中的任意向量在变换后直接投影在数轴上(这里要注意,向量在变换后变成了数轴上仅用一个数字表示的值,它已经不是一个二维向量,此时在二维平面内看它毫无意义,将数轴放到二维平面目的是让这个变换更加直观)。
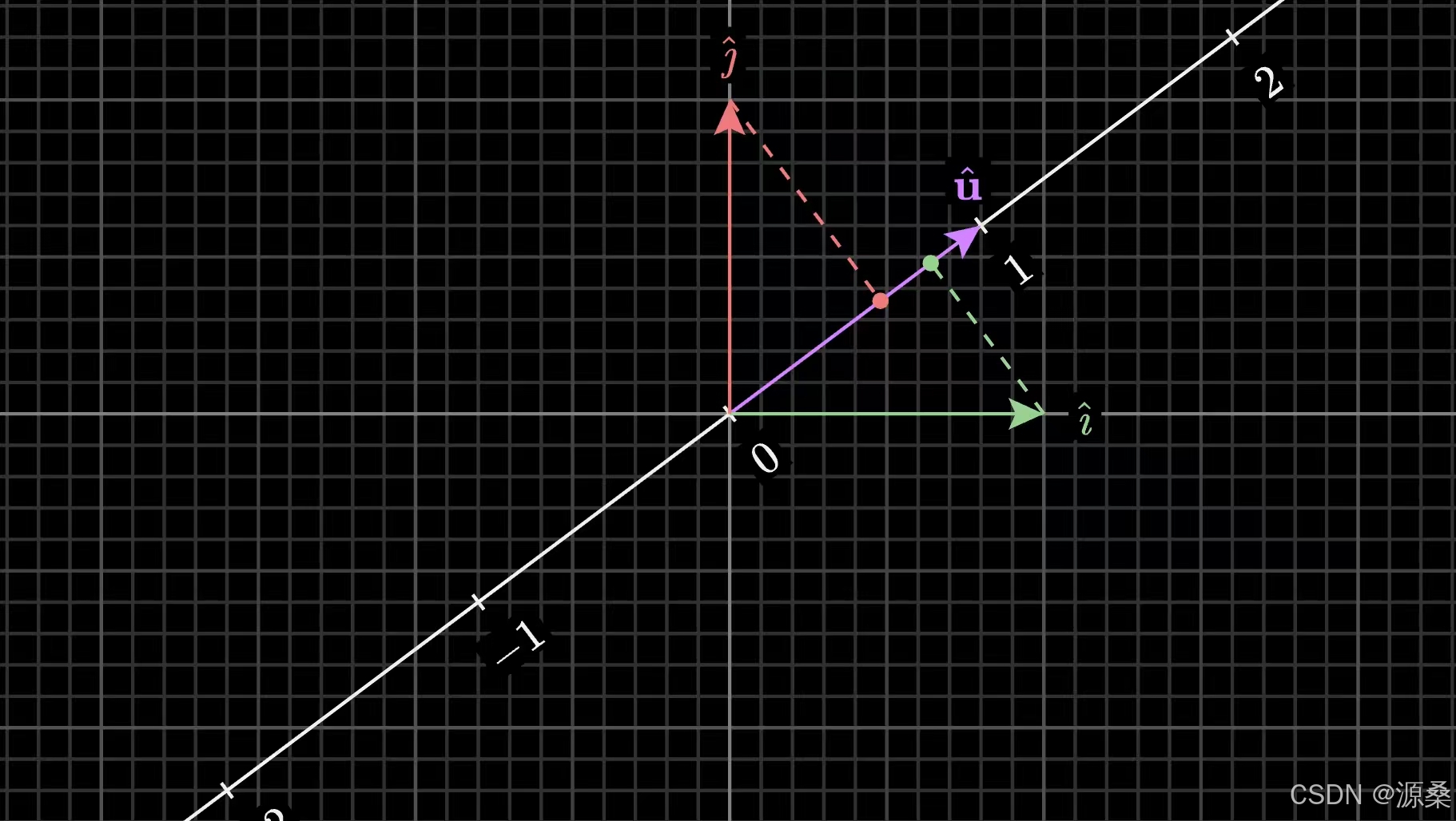
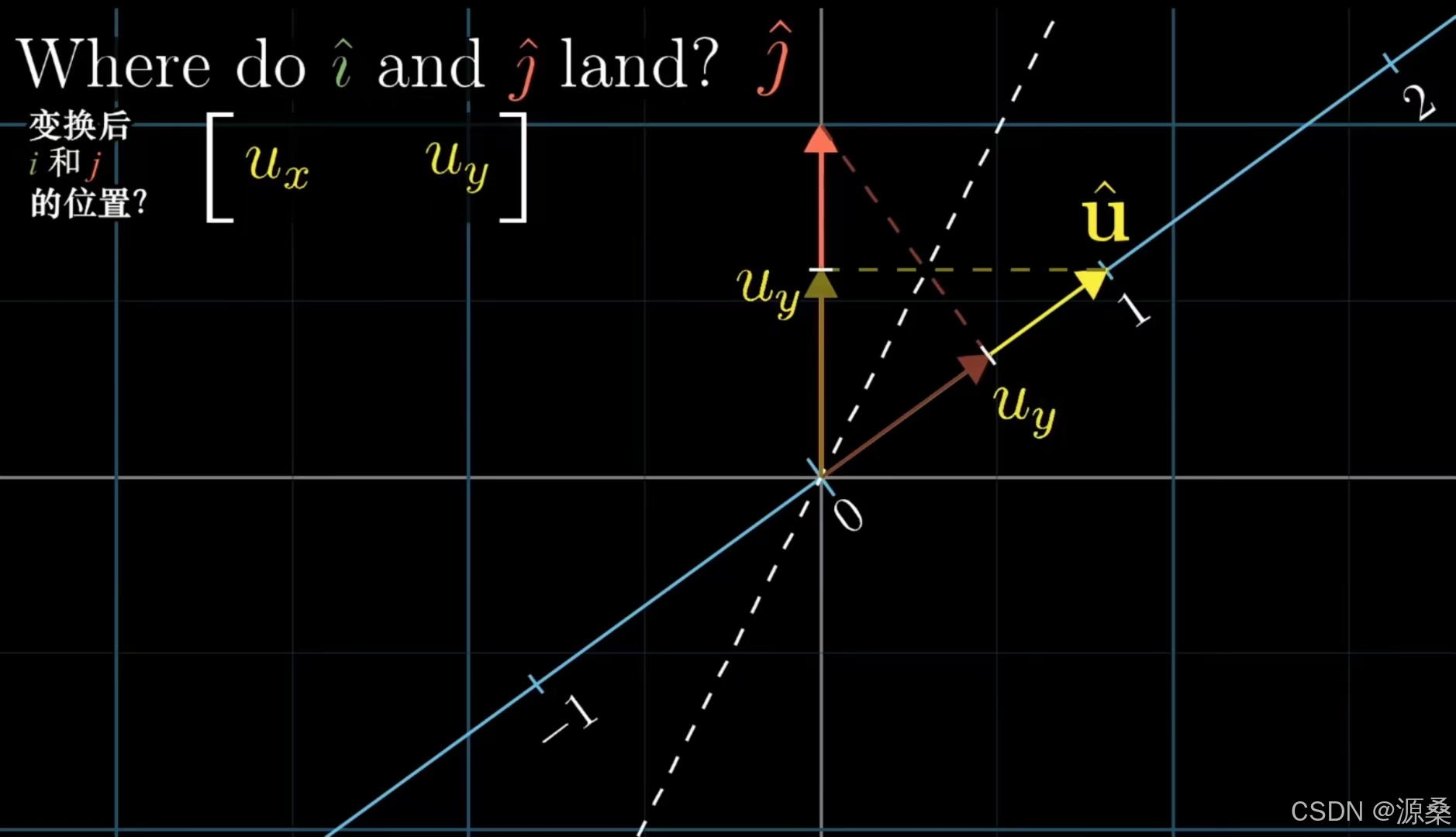
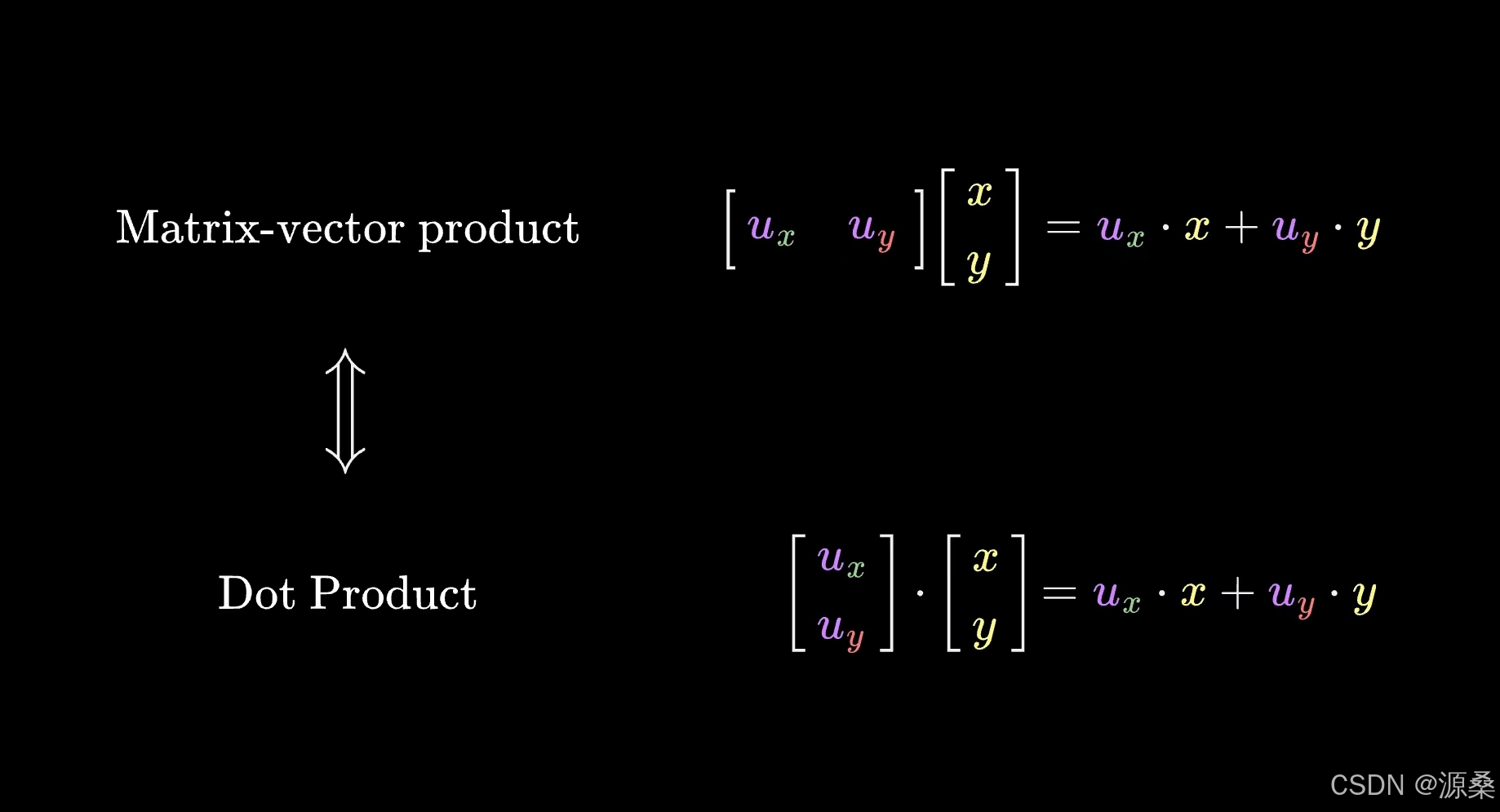
为了描述这一变换,们先考虑平面内两个坐标轴上的基向量i、j的变换,假设平面中恰好存在一个单位向量U与数轴重合,我由对称性质可以得到:向量i变换后在数轴上的长度等于单位向量U投影到横轴上的长度,因此i变换后的i’就是向量u的横坐标Ux。同理j变换后的j‘就是向量U的纵坐标Uy,这样我们就得到了这一变换的矩阵[Ux, Uy]。这时可以发现计算矩阵向量乘积的计算过程与点积完全一致,这就是为什么与单位向量点积可以解读为向量在单位向量上投影的长度。
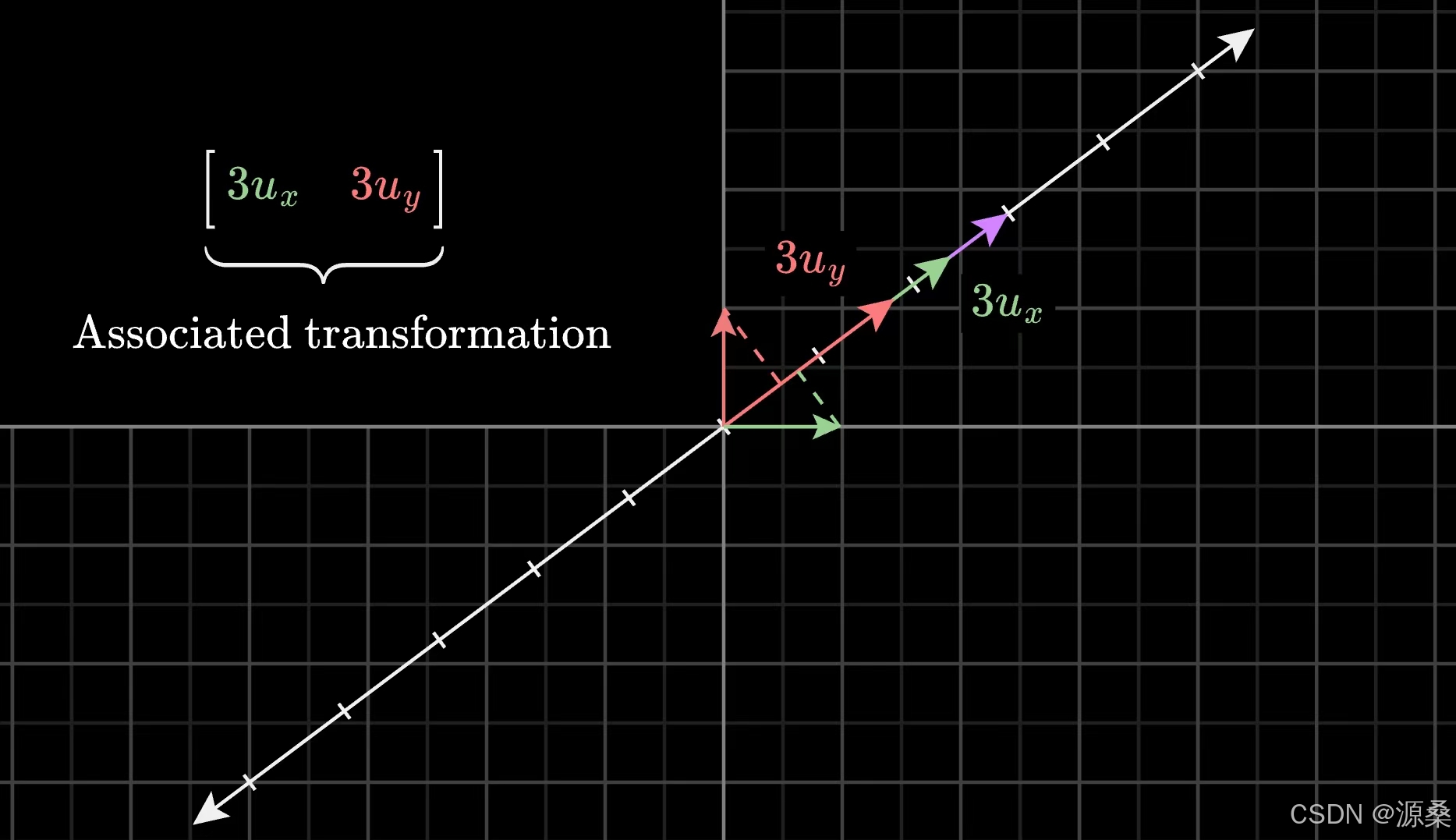
其次我们再考虑U不是单位向量的情况,如果要寻找与这个向量相关的投影矩阵,实际上就是先前由单位向量得到的矩阵的倍数。这就是为什么两个向量的点积就是一个向量先投影到另一个向量,再将投影的长度乘以另一个向量的长度(这里的长度就是相对于单位向量的倍数)。
回顾整个过程,首先我们定义了一个从二维平面到一维数轴的变换,这个变换过程仅仅是将向量投影到数轴上,因为变换是线性的,所以这个过程必然可以用一个1x2的矩阵表示,又因为1x2的矩阵与二维向量乘积的计算过程和该矩阵的转置与二维向量的点积的计算过程相同,所以二维平面内一定有一个向量的转置就是1x2矩阵。
综上:任何一个线性变换,如果他的输出空间是一维的,空间中会存在唯一的向量v与之相关,这时应用线性变换和与向量v(实际上就是该线性变换矩阵的转置,称之为对偶向量)做点积是一样的。
ps:这是对偶性的一个实例,我觉得这个过程非常amazing!
如果我的表述存在问题或者你也有自己的看法,欢迎大家在评论区讨论!
























 2661
2661

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








