PyTorch实例：预测房价

这个实例问题是：假如有历史房价数据，我们应如何预测未来某一天的房价？针对这个问题，我们的求解步骤包括：准备数据、设计模型、训练和预测。

准备数据

我们需要找到真实的房价数据来进行拟合和预测。简单起见，我们也可以人为编造一批数据，从而重点关注方法和流程。首先，我们编造一批时间数据。假设我们每隔一个月能获得一次房价数据，那么时间数据就可以为0, 1, …，表示第0、1、2……个月份，我们可以用PyTorch的linspace来构造0~100之间的均匀数字作为时间变量$x$：

x = torch.linspace(0,100,100).type(torch.FloatTensor) # 生成100个数据

然后，我们再来编造这些时间点上的历史房价数据。假设它就是在x的基础上加上一定的噪声：

rand =torch.randn(100)* 10
y = x + rand

这里的rand是一个随机数，满足均值为0、方差为10的正态分布。torch.randn(100)这个命令可以生成100个满足标准正态分布的随机数（均值为0，方差为1）。于是，我们就编造好了历史房价数据：$y$。
现在我们有了100个时间点$x_i$和每个时间点对应的房价$y_i$。其中$x_i{y}_i$被称为一个样本点。
之后我们将数据集分为训练集和测试集两部分。
所谓训练集，是指训练一个模型的所有数据；所谓测试集，则是指用于检验这个训练好的模型的所有数据。注意，在训练过程中，模型不会接触到测试集的数据。因此，模型在测试集上运行的效果模拟了真实的房价预测环境。
在下面这段代码中，:-10是指从$x$变量中取出倒数第10个元素之前的所有元素；而-10:是指取出$x$中倒数10个元素。所以，我们就把第0到第90个月的数据当作训练集，把后10个月的数据当作测试集:

x_train = x[: -10]
x_test = x[-10 :]
y_train = y[: -10]
y_test = y[-10 :]

接下来我们对训练的数据进行可视化：

import matplotlib.pyplot as plt # 导入画图的程序包

plt.figure(figsize=(10,8)) # 设定绘制窗口大小为10×8 inch
# 绘制数据，由于x和y都是自动微分变量，因此需要用data获取它们包裹的tensor，并转成NumPy 
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'o')
plt.xlabel('X') # 添加X轴的标注
plt.ylabel('Y') # 添加Y轴的标注
plt.show() # 画出图形

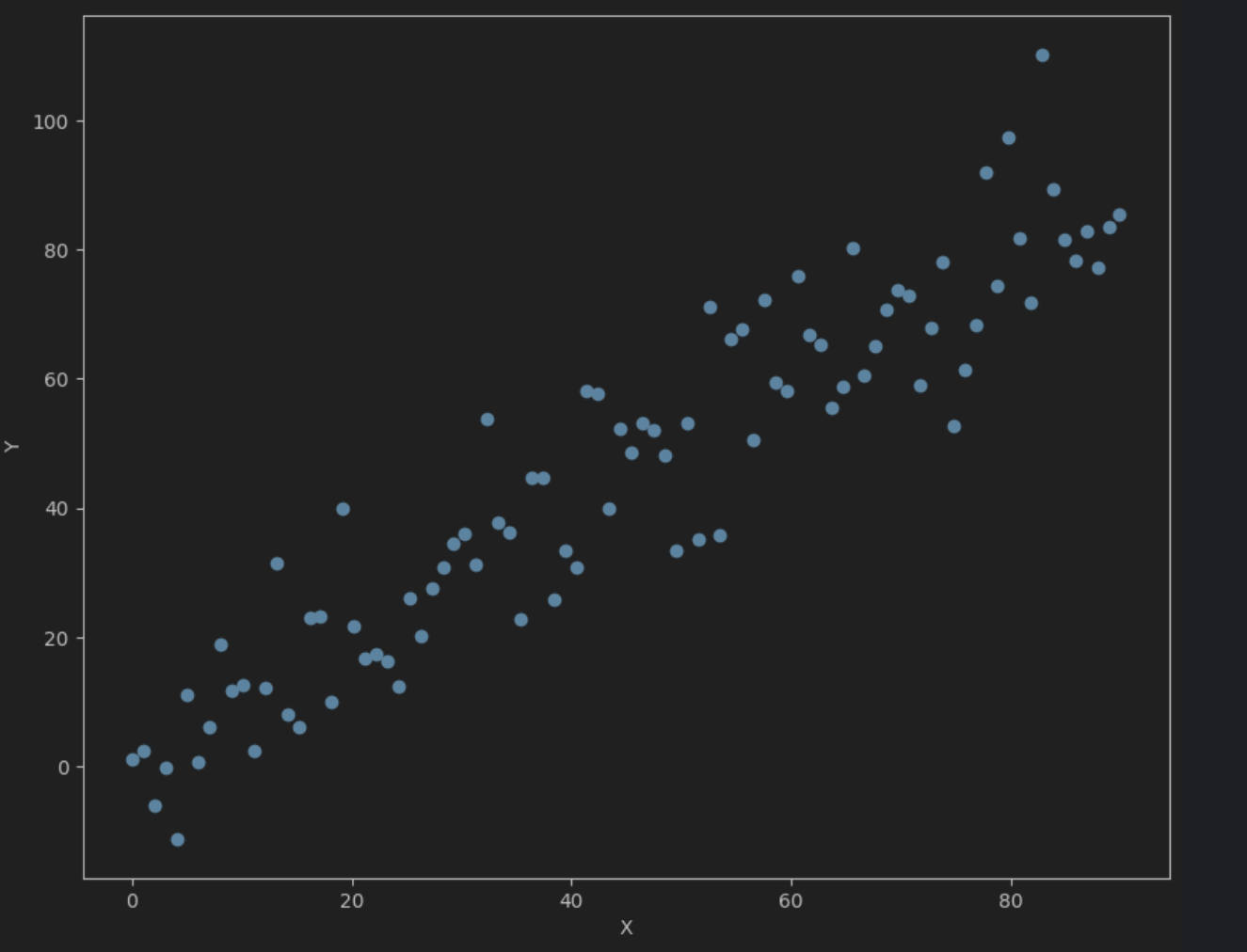
通过观察散点图，可以看出走势呈线性，所以可以用线性回归来进行拟合。

模型设计

我们希望得到一条尽可能从中间穿越这些数据散点的拟合直线。设这条直线方程为：
$y=ax+b$
接下来就是求解参数$a$和$b$的值。我们可以将每一个数据点$x_i$带入，得到${\hat{y}}_i$,
${\hat{y}}_i=a{x}_i+b$
显然，这个点越靠近$y_i$越好。所以我们定义一个平均损失函数：
$L=\frac{1}{N}{\sum }_i^N(y_i-{\hat{y}}_i{)}^2=\frac{1}{N}{\sum }_i^N(y_i-a{x}_i-b{)}^2$
并让它尽可能地小。其中$N$为所有数据点的个数，也就是100。由于$x_i$和$y_i$都是固定的数，而只有$a$和$b$是变量，那么$L$本质上就是$a$和$b$的函数。所以，我们要寻找最优的$a$、$b$组合，让$L$最小化.
我们可以利用梯度下降法来反复迭代$a$和$b$，从而让$L$越变越小。梯度下降法是一种常用的数值求解函数最小值的方法，它的基本思想就像是盲人下山,这里要优化损失函数$L(a,b)$.
假设有一个盲人站在山上的某个随机初始点（这就对应了$a$和$b$的初始随机值），他会在原地转一圈，寻找下降最快的方向来行进。所谓下降的快慢，其实就是$L$对$a$、$b$　在这一点的梯度（导数）；所谓的行进，就是更新$a$和$b$的值，让盲人移动到一个新的点。于是，每到一个新的点，盲人就会依照同样的方法行进，最终到达让$L$最小的那个点。
我们可以通过下面的迭代计算来实现盲人下山的过程：
$$\begin{gathered} a_{t+1}=a_t-\alpha \frac{\partial L}{\partial a}|a=a_t \\ {b}_{t+1}=b_t-\alpha \frac{\partial L}{\partial b}|b=b_t \end{gathered}$$
$\alpha$为一个参数，叫做学习率，它可以调节更新的快慢，相当于盲人每一步的步伐有多大。$\alpha$越大，$a$,$b$更新得越快，但是计算得到的最优值$L$就可能越不准确。
在计算的过程中,我们需要计算出$L$对$a$、$b$的偏导数,利用PyTorch的$backward()$可以非常方便地将这两个偏导数计算出来。于是,我们只需要一步一步地更新$a$和$b$的数值就可以了。当达到一定的迭代步数之后,最终的$a$和$b$的数值就是我们想要的最优数值, $y=ax+b$这条直线就是我们希望寻找的尽可能拟合所有数据点的直线。

训练

接下来，我们将上述思路转化为PyTorch代码。首先，我们需要定义两个自动微分变量$a$和$b$：

a = torch.rand(1, requires_grad = True)
b = torch.rand(1, requires_grad = True)

可以看到，在初始的时候，$a$和$b$都是随机取值的。设置学习率：

learning_rate = 0.0001

然后，完成对a和b的迭代计算：

for i in range(1000):
# 计算在当前a、b条件下的模型预测值
    predictions = a.expand_as(x_train) * x_train + b.expand_as(x_train)
    # 将所有训练数据代入模型ax+b，计算每个的预测值。这里的x_train和predictions都是(90, 1)的张量
    # Expand_as的作用是将a、b扩充维度到和x_train一致
    loss = torch.mean((predictions - y_train) ** 2) # 通过与标签数据y比较计算误差，loss是一个标量
    print('loss:', loss)
    loss.backward() # 对损失函数进行梯度反传
    # 利用上一步计算中得到的a的梯度信息更新a中的data数值
    a.data.add_(- learning_rate * a.grad.data)
    # 利用上一步计算中得到的b的梯度信息更新b中的data数值
    b.data.add_(- learning_rate * b.grad.data)
    # 增加这部分代码，清空存储在变量a、b中的梯度信息，以免在backward的过程中反复不停地累加
    a.grad.data.zero_() # 清空a的梯度数值
    b.grad.data.zero_() # 清空b的梯度数值

这个迭代计算了1000次，当然，我们可以调节数值，数值越大理论上计算得到的$a$$b$的值越准确。
在每一步计算的过程中，我们首先计算$predictions$,及所有点的${\hat{y}}_i$;然后计算平均误差函数$loss$，及前面定义的$L$；接着调用了$backward()$函数，求$L$对计算图中所有叶节点$(a,b)$的导数。于是这些导数信息分别存储在了$a.grad$以及$b.grand$之中；随后，通过$a.data.add\_(-learning\_rate\ast a.grad.data)$完成了对$a$的数值更新，也就是$a$的数值应该加上一个$-learning\_rate$乘以刚刚计算得到的$L$对$a$的偏导数值，$b$也是同样的道理；最后在更新完$a$$b$的数值后，需要清空它们的梯度信息，否则它会在下一步迭代的时候自动累加而导致错误。
**整个计算过程其实是利用自动微分变量 **$a$和$b$来完成动态计算图的构建，然后在其上进行梯度反传的过程。所以，整个计算过程就是在训练一个广义的神经网络，a和b就是神经网络的参数，一次迭代就是一次训练。

• 在计算$predictions$时,为了让$a$、$b$与$x$的维度相匹配,我们对$a$和$b$进行了扩维。我们知道$x\_train$的尺寸是$(90,1)$,而$a$、$b$的尺寸都是$1$,它们并不匹配。我们可以通过$expand\_as$增大$a$、$b$的尺寸,与$x\_train$一致。$a.expandas(xtrain)$的作用是将$a$的维度调整为和$x\_train$一致,所以函数的结果是得到一个尺寸为$(90,1)$的张量,张量中的数值全为$a$。
• PyTorch规定，不能直接对自动微分变量进行数值更新，只能对它的$data$属性进行更新。所以在更新$a$的时候，我们是在更新$a.data$，也就是$a$所包裹的张量。
• 在PyTorch中，如果某个函数后面加上了“_”，就表明要用这个函数的计算结果更新当前的变量。例如，$a.data.ad{d}_{(}3)$的作用是将$a.data$的数值更新为$a.data$加上3。

最后，将原始的数据散点联合拟合的直线画出来，如下所示：

x_data = x_train.data.numpy()  # 将x中的数据转换成NumPy数组
plt.figure(figsize = (10, 7))    # 定义绘图窗口
xplot, = plt.plot(x_data, y_train.data.numpy(), 'o')      # 绘制x和y的散点图
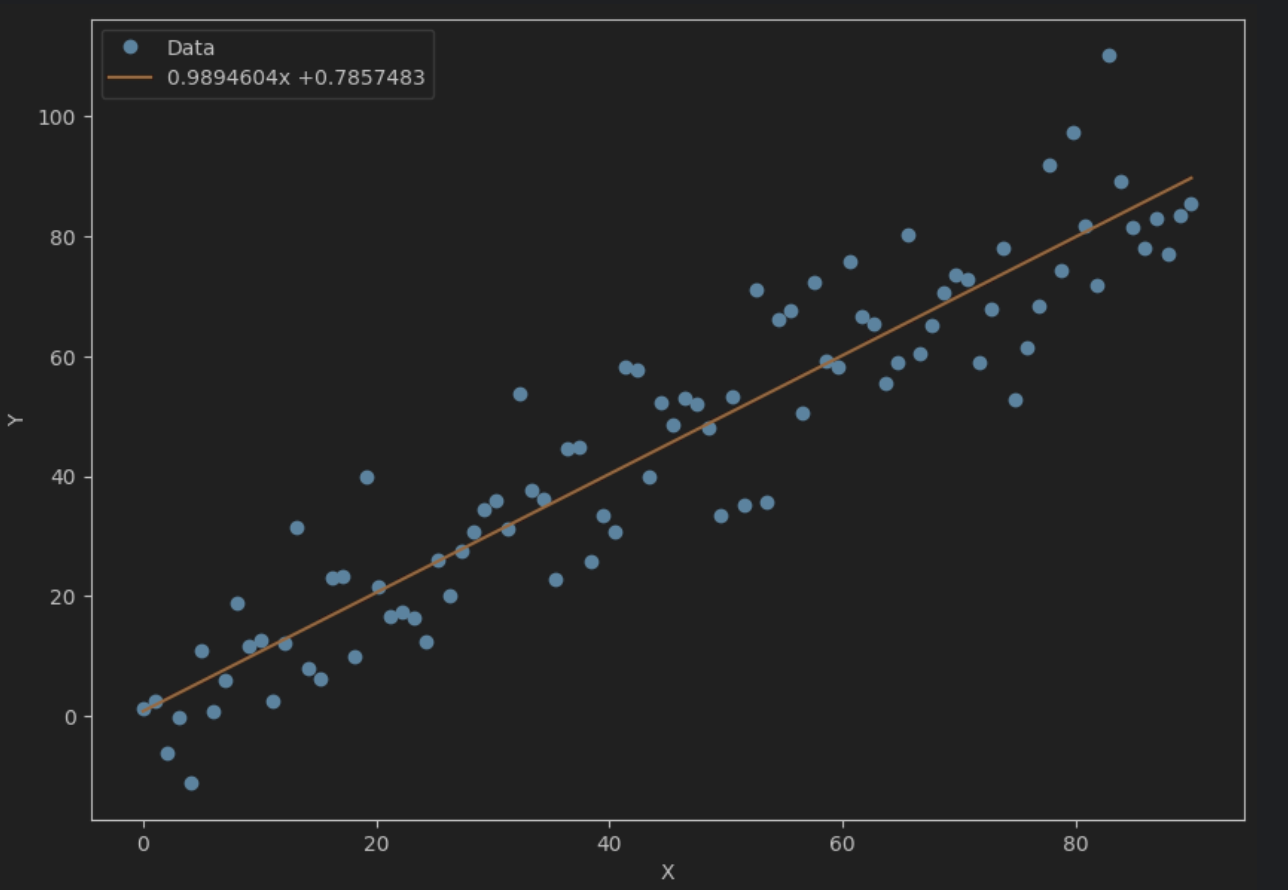
yplot, = plt.plot(x_data, a.data.numpy() * x_data +b.data.numpy())     # 绘制拟合直线图
plt.xlabel('X')      # 给横坐标轴加标注
plt.ylabel('Y')      # 给纵坐标轴加标注
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0])      # 将拟合直线的参数a、b显示出来
plt.legend([xplot, yplot],['Data', str1])      # 绘制图例
plt.show() # 绘制图形

预测

最后一步就是进行预测。在测试数据集上应用我们拟合的直线来预测对应的$y$，也就是房价。只需要将测试数据的$x$值带入我们拟合的直线即可:

predictions = a.expand_as(x_test) * x_test + b.expand_as(x_test) # 计算模型的预测结果
predictions # 输出

那么，预测结果到底准不准呢？我们不妨把预测数值和实际数值绘制在一起，如下所示：

x_data = x_train.data.numpy() # 获得x包裹的数据
x_pred = x_test.data.numpy() # 获得包裹的测试数据的自变量
plt.figure(figsize = (10, 7)) # 设定绘图窗口大小
plt.plot(x_data, y_train.data.numpy(), 'o') # 绘制训练数据
plt.plot(x_pred, y_test.data.numpy(), 's') # 绘制测试数据
x_data = np.r_[x_data, x_test.data.numpy()]
plt.plot(x_data, a.data.numpy() * x_data + b.data.numpy())  # 绘制拟合数据
plt.plot(x_pred, a.data.numpy() * x_pred + b.data.numpy(), 'o') # 绘制预测数据
plt.xlabel('X') # 更改横坐标轴标注
plt.ylabel('Y') # 更改纵坐标轴标注
str1 = str(a.data.numpy()[0]) + 'x +' + str(b.data.numpy()[0]) # 图例信息
plt.legend([xplot, yplot],['Data', str1]) # 绘制图例
plt.show()

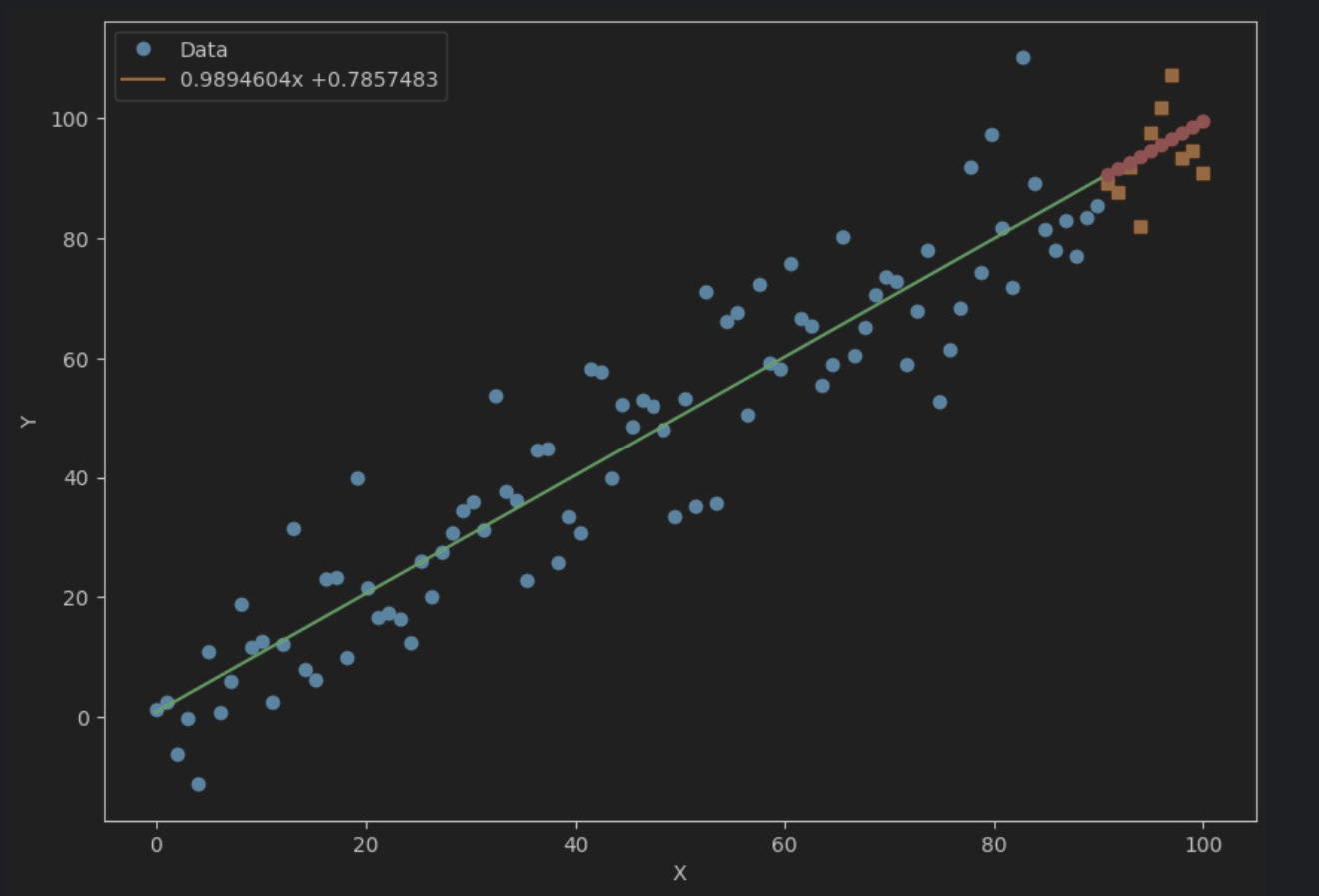
方块点表示测试集中实际的房价数据，直线上的圆点则表示在测试集上预测的房价数据
我们通过线性回归以及其他的简单示例代码展示了PyTorch的迷人优点：支持张量的计算和动态计算图，具有Python化的编程风格。总的来看，PyTorch可以利用自动微分变量将一般的计算过程全部自动转化为动态计算图。所以，一个完整的算法就可以搭建一个计算图，也就是一个广义的神经网络。之后可以利用PyTorch强大的$backward$功能自动求导，利用复杂的计算图进行梯度信息的反传，从而计算出每个叶节点对应的自动微分变量的梯度信息。有了这种值，我们就可以利用梯度下降算法来更新参数，也就是广义的训练或学习的过程。因此，PyTorch可以非常方便地将学习问题自动化。