考研数学积分学

一.一元函数积分学的概念与性质

1.不定积分

（1）原函数与不定积分

（2）原函数（不定积分）存在定理

• 连续函数必有原函数
• 含有第一类间断点和无穷间断点的函数，在包含该断点的区间内没有原函数
• 震荡间断点不一定有
  • 震荡间断点不一定是间断的，如果间断点的函数极限和那点的函数值相等，那么说明不是真的断了，是连续的，所以有原函数
  • 如果间断点的函数极限和那点的函数值不等，那么说明是真的断了，不是连续的，所以没有原函数

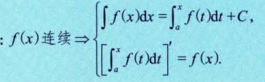
（3）f(x)与f'(x)区别

• 连续
  • f(x)在x=x0处的极限存在，不能得出f(x)在x=x0处连续
  • f(x)可导，且导函数的极限存在，能得出f‘(x)在x=x0处连续
• 介值
  • f(x)存在，不能得出f(x)有介值性
  • f’(x)存在，能得出f‘(x)有介值性

2.定积分

（1）定义

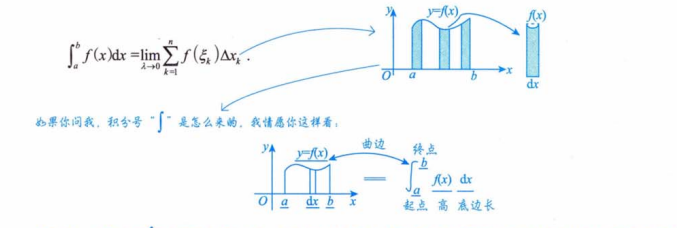
重要公式

注：定积分的值只与被积函数及积分区间有关，而与积分变量的是谁无关

（2）存在定理

充分条件

• f(x)在[a,b]上连续，则存在
• f(x)在[a,b]上单调，则存在
• f(x)在[a,b]上有界，且只有有限的间断点（不包含无穷间断点），则存在
• f(x)在[a,b]上有有限的第一类间断点，则存在

必要条件

• 可积函数必有界，若存在，则f（x）在[a,b]必有界

（3）性质

• 当b = a时，=0;
• 当b < a时，=-;(交换上下限填负号)
• 性质

重要不等式

3.变限积分

（1）概念

（2）性质

偶函数的变限积分是奇函数，奇函数的变限积分是偶函数

4.反常积分

（1）概念

（2）判是否收敛

二.一元函数积分学的计算

1.基本积分公式

2.不定积分的积分法

3.定积分的积分法

4.变限积分的计算

5.反常积分的计算

三.一元函数积分学的应用（1）

1.平面图形的面积

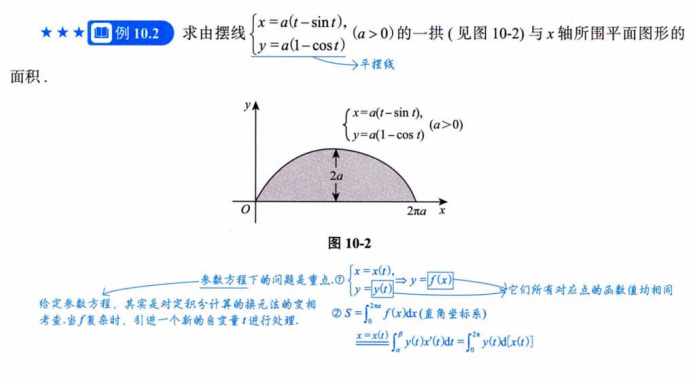
2.旋转体的体积

3.函数的平均值

4.其他几何应用

四.一元函数积分学的应用（2）

1.积分等式

2.积分不等式

五.一元函数积分学的应用（3）