机器学习6-支持向量机

最新推荐文章于 2024-06-11 16:13:44 发布

小趴菜️

最新推荐文章于 2024-06-11 16:13:44 发布

阅读量1.4k

点赞数 43

文章标签：机器学习支持向量机人工智能

本文链接：https://blog.csdn.net/qq_74065190/article/details/139303989

版权

一、什么是SVM

1、简介

SVM（支持向量机）是一种常见的监督学习算法，用于分类和回归问题。

考虑一个二分类问题：假设输入空间与特征空间为两个不同的空间，这两个空间的元素一一对应，并将输入空间的输入映射为特征空间中的特征向量，支持向量机的学习是在特征空间进行的。

在分类问题中，SVM通过在特征空间中找到一个最优的超平面来将不同类别的数据分隔开。在回归问题中，SVM通过寻找一个最优的超平面来拟合数据点，使得尽可能多的数据点位于超平面的边界上。

SVM的核心思想是将原始特征映射到一个高维特征空间，并在该空间中找到一个最优的超平面。为了找到最优的超平面，SVM采用了两个关键概念：间隔和支持向量。间隔表示超平面到最近的训练样本的距离，SVM的目标是找到具有最大间隔的超平面。支持向量是离超平面最近的训练样本点，它们对于定义超平面起到关键作用。

SVM算法可以使用不同的核函数，如线性核、多项式核和高斯核，来处理非线性的分类问题。这些核函数可以将数据从原始特征空间映射到一个更高维的特征空间，在新的特征空间中进行线性分类或回归。

简单概括为以下几点：

1.寻找最优的超平面：SVM 的目标是在特征空间中找到一个最优的超平面，以能够将不同类别的样本正确地分开。超平面是一个 d-1 维的子空间，其中 d 是特征空间的维度。

2.最大化间隔：SVM 在寻找超平面时，会尽可能地将不同类别的样本分开，并且使得支持向量（离超平面最近的样本点）到超平面的距离最大化。这个距离被称为间隔（margin），因此 SVM 也被称为最大间隔分类器。

3.核函数技巧：当样本数据线性不可分时，SVM 通过引入核函数来将数据映射到高维特征空间，从而使得非线性问题在高维空间中变得线性可分。常用的核函数有线性核、多项式核、高斯径向基函数（RBF）核等。

4.支持向量：在 SVM 中，只有少数关键的样本点对确定超平面起作用，这些样本点被称为支持向量。SVM 的决策边界只与支持向量有关，而与其他样本点无关，这也是 SVM 算法高效的原因之一。

5.正则化参数 C：SVM 中的正则化参数 C 控制了模型的复杂度与容错能力之间的权衡。较小的 C 值会使得分类器更加允许出现错误分类，使得决策边界更加平滑；而较大的 C 值会强制分类器尽可能正确分类所有样本，可能导致过拟合。

2、线性可分与线性不可分

线性可分如图左，不可分右

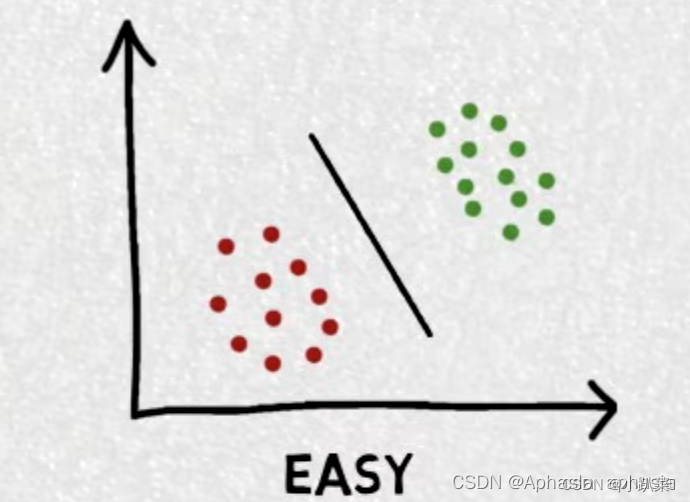
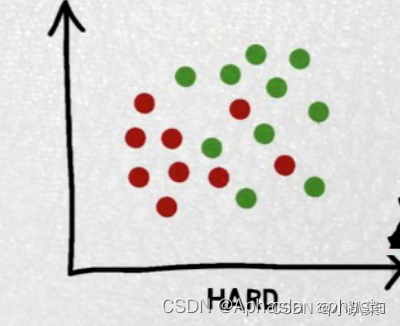
在线性可分问题中，可以通过求解一个凸优化问题来寻找最优的超平面。这个问题的目标是最大化间隔，并且要满足所有正样本和负样本的约束条件。

然而，实际应用中，许多问题并不是线性可分的，即使使用直线或平面也无法完全将不同类别的样本分开。这时候就需要引入一些方法来处理线性不可分问题。

一种常用的方法是引入松弛变量（slack variable），它允许样本出现错误分类。通过引入松弛变量，可以允许一些样本位于超平面的错误一侧，从而使得分类器具有容错能力。

线性不可分问题可以通过引入软间隔 SVM（Soft Margin SVM）来解决。软间隔 SVM 允许一些样本位于超平面的边界区域，同时尽可能地减小松弛变量的数量。这样可以在保持分类器简单性和泛化能力的同时，允许一些错误的分类。

另外，当线性不可分问题无法通过低维空间的超平面进行划分时，可以使用核函数。核函数可以将样本映射到高维特征空间，使得非线性问题在高维空间中变得线性可分。常用的核函数有线性核、多项式核、高斯径向基函数（RBF）核等。

二、寻找最大间隔

1、找到最好的参数

（1）什么是好的参数

支持向量机的核心思想：最大间隔化，最不受到噪声的干扰。如上图所示，分类器A比分类器B的间隔（蓝色阴影）大，因此A的分类效果更好。

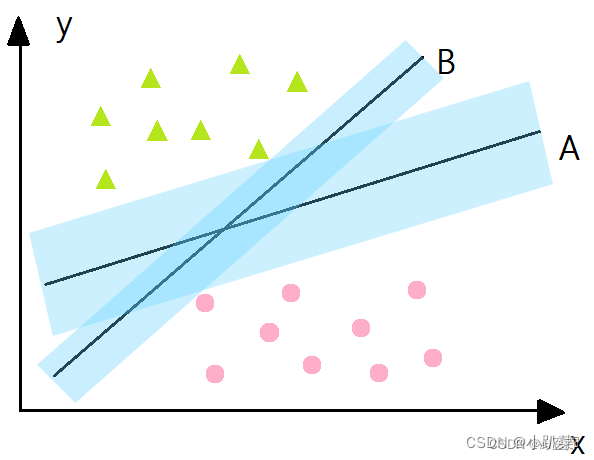
（2）如何找到

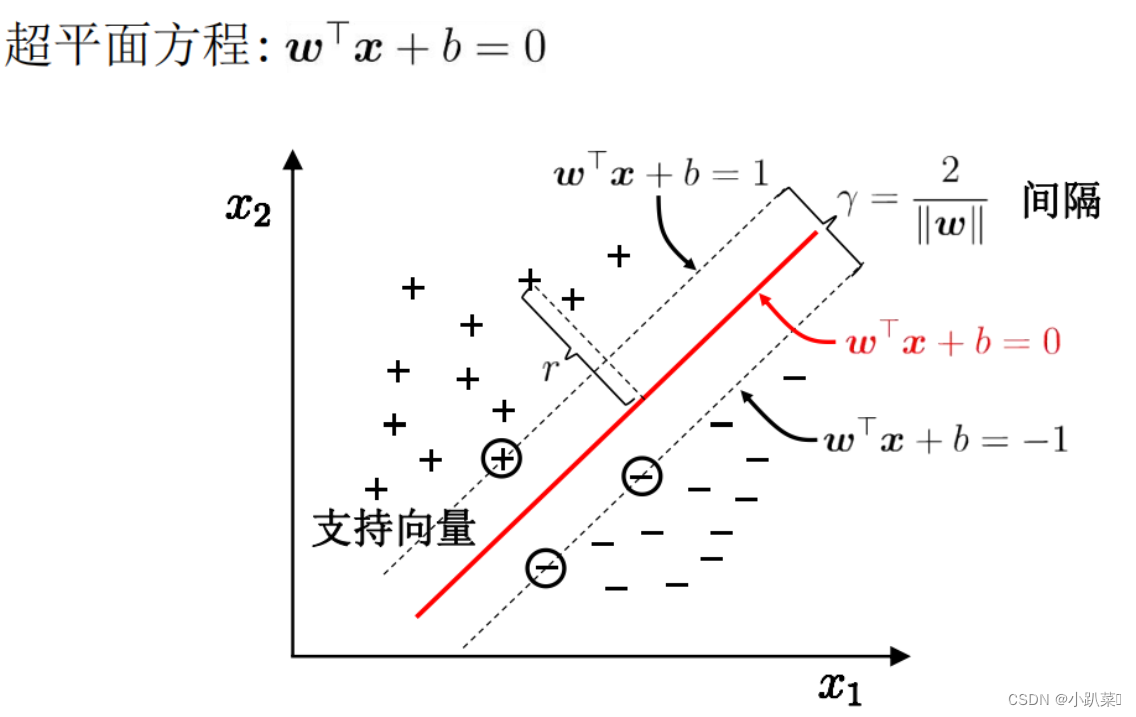
数学上，对于一个线性可分的二分类问题，可以用以下形式的方程表示超平面：

$w^{t}\times x+b=0$

其中：

X 为训练样本

b 为位移项，决定了超平面与原点之间的距离

r等同于d

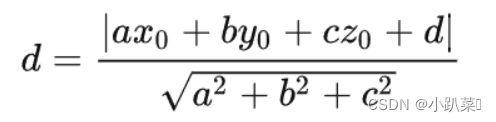
（3）应用实例

寻找支持向量

# sklearn 库中导入 svm 模块
from sklearn import svm

# 定义三个点和标签
X = [[2, 0], [1, 1], [2,3]]
y = [0, 0, 1]
# 定义分类器，clf 意为 classifier，是分类器的传统命名
clf = svm.SVC(kernel = 'linear')  # .SVC（）就是 SVM 的方程，参数 kernel 为线性核函数
# 训练分类器
clf.fit(X, y)  # 调用分类器的 fit 函数建立模型（即计算出划分超平面，且所有相关属性都保存在了分类器 cls 里）
# 打印分类器 clf 的一系列参数
print(clf)
# 支持向量
print(clf.support_vectors_)
# 属于支持向量的点的 index 
print(clf.support_)
# 在每一个类中有多少个点属于支持向量
print(clf.n_support_) 
# 预测一个新的点
print(clf.predict([[2,0]]))

输出结果：

# 打印分类器 clf 的一系列参数
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
  kernel='linear', max_iter=-1, probability=False, random_state=None,
  shrinking=True, tol=0.001, verbose=False)
# 支持向量
[[1. 1.]
 [2. 3.]]
# 属于支持向量的点的 index
[1 2]
# 在每一个类中有多少个点属于支持向量
[1 1]
# 预测一个新的点
[0]

对于线性可分问题的实现

print(__doc__)
# 导入相关的包
import numpy as np
import pylab as pl  # 绘图功能
from sklearn import svm

# 创建 40 个点
np.random.seed(0) # 让每次运行程序生成的随机样本点不变
# 生成训练实例并保证是线性可分的
# np._r表示将矩阵在行方向上进行相连
# random.randn(a,b)表示生成 a 行 b 列的矩阵，且随机数服从标准正态分布
# array(20,2) - [2,2] 相当于给每一行的两个数都减去 2
X = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]
# 两个类别 每类有 20 个点，Y 为 40 行 1 列的列向量
Y = [0] * 20 + [1] * 20

# 建立 svm 模型
clf = svm.SVC(kernel='linear')
clf.fit(X, Y)

# 获得划分超平面
# 划分超平面原方程：w0x0 + w1x1 + b = 0
# 将其转化为点斜式方程，并把 x0 看作 x，x1 看作 y，b 看作 w2
# 点斜式：y = -(w0/w1)x - (w2/w1)
w = clf.coef_[0]  # w 是一个二维数据，coef 就是 w = [w0,w1]
a = -w[0] / w[1]  # 斜率
xx = np.linspace(-5, 5)  # 从 -5 到 5 产生一些连续的值（随机的）
# .intercept[0] 获得 bias，即 b 的值，b / w[1] 是截距
yy = a * xx - (clf.intercept_[0]) / w[1]  # 带入 x 的值，获得直线方程

# 画出和划分超平面平行且经过支持向量的两条线（斜率相同，截距不同）
b = clf.support_vectors_[0] # 取出第一个支持向量点
yy_down = a * xx + (b[1] - a * b[0]) 
b = clf.support_vectors_[-1] # 取出最后一个支持向量点
yy_up = a * xx + (b[1] - a * b[0])

# 查看相关的参数值
print("w: ", w)
print("a: ", a)
print("support_vectors_: ", clf.support_vectors_)
print("clf.coef_: ", clf.coef_)

# 在 scikit-learin 中，coef_ 保存了线性模型中划分超平面的参数向量。形式为(n_classes, n_features)。若 n_classes > 1，则为多分类问题，(1，n_features) 为二分类问题。

# 绘制划分超平面，边际平面和样本点
pl.plot(xx, yy, 'k-')
pl.plot(xx, yy_down, 'k--')
pl.plot(xx, yy_up, 'k--')
# 圈出支持向量
pl.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
           s=80, facecolors='none')
pl.scatter(X[:, 0], X[:, 1], c=Y, cmap=pl.cm.Paired)

pl.axis('tight')
pl.show()

输出结果

三、核函数

1、简介

映射可以看作是一种拉伸，把低维数据拉伸到了高维。虽然现在我们到了高维空间号称线性可分，但是有几个困难：

不知道什么样的映射函数是完美的。
难以在各种映射函数中找到一个合适的。
高维空间计算量比较大。这样就会产生维灾难，计算内积是不现实的。

幸运的是，在计算中发现，我们需要的只是两个向量在新的映射空间中的内积结果，而映射函数到底是怎么样的其实并不需要知道。于是这样就引入了核函数的概念。

核函数事先在低维上计算，而将实质上的分类效果表现在了高维上，也就是

包含映射，内积，相似度的逻辑。
消除掉把低维向量往高维映射的过程。
避免了直接在高维空间内的复杂计算。

即核函数除了能够完成特征映射，而且还能把特征映射之后的内积结果直接返回。即把高维空间得内积运算转化为低维空间的核函数计算。

注意，核函数只是将完全不可分问题，转换为可分或达到近似可分的状态。

在实际中，我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去，但如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的，此时就需要使用核函数。核函数虽然也是将特征进行从低维到高维的转换，但核函数会先在低维上进行计算，而将实质上的分类效果表现在高维上，避免了直接在高维空间中的复杂计算。

如下图所示的两类数据，这样的数据本身是线性不可分的，当我们将二维平面的坐标值映射一个三维空间中，映射后的结果可以很明显地看出，数据是可以通过一个平面来分开的。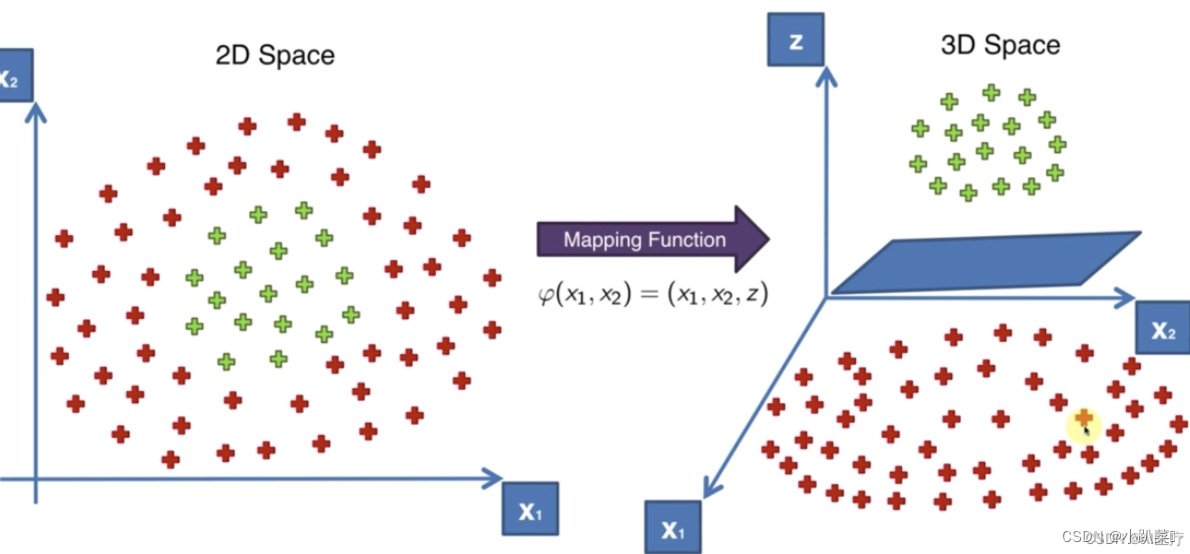

核函数方法处理非线性问题的基本思想：按一定的规则进行映射，使得原来的数据在新的空间中变成线性可分的，从而就能使用之前推导的线性分类算法进行处理。计算两个向量在隐式映射过后的空间中的内积的函数叫做核函数

2、计算

φ(x)是把训练集中的向量点转化到高维的非线性映射函数，变量x和y在新空间中，二者分别对应φ(x)和φ(y)，他们的内积则为<φ(x),φ(y)>。

我们令函数Kernel(x,y)=<φ(x),φ(y)>=k(x,y)，则称Κ(x,y)为核函数，φ(x)为映射函数

可以看出，函数Kernel(x,y)是一个关于x和y的函数！而与φ无关！这是一个多么好的性质！我们再也不用管φ具体是什么映射关系了，只需要最后计算Kernel(x,y)就可以得到他们在高维空间中的内积。

我们大致能够得到核函数如下性质：

核函数给出了任意两个样本之间关系的度量，比如相似度。
每一个能被叫做核函数的函数，里面都藏着一个对应拉伸的函数。这些核函数的命名通常也跟如何做拉伸变换有关系。
核函数和映射本身没有直接关系。选哪个核函数，实际上就是在选择用哪种方法映射。通过核函数，我们就能跳过映射的过程。
我们只需要核函数，而不需要那个映射，也无法显式的写出那个映射。
选择核函数就是把原始数据集上下左右前后拉扯揉捏，直到你一刀下去正好把所有的 0 分到一边，所有的 1 分到另一边。这个上下左右前后拉扯揉捏的过程就是kernel.

2、常见的核函数

通过前面的介绍，核函数的选择，对于非线性支持向量机的性能至关重要。但是由于我们很难知道特征映射的形式，所以导致我们无法选择合适的核函数进行目标优化。于是“核函数的选择”称为支持向量机的最大变数，我们常见的核函数有以下几种：

此外，还可以通过函数组合得到，例如：

对于非线性的情况，SVM 的处理方法是选择一个核函数 κ(⋅,⋅)，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。由于核函数的优良品质，这样的非线性扩展在计算量上并没有比原来复杂多少，这一点是非常难得的。当然，这要归功于核方法——除了 SVM 之外，任何将计算表示为数据点的内积的方法，都可以使用核方法进行非线性扩展。

3、实例

四、拓展到多分类问题

SVM 扩展可解决多个类别分类问题：
对于每个类，有一个当前类和其他类的二类分类器（one-vs-rest）
将多分类问题转化为 n 个二分类问题，n 就是类别个数。

SVM 算法特性
训练好的模型的算法复杂度是由支持向量的个数决定的，而不是由数据的维度决定的。所以 SVM 不太容易产生 overfitting。
SVM 训练出来的模型完全依赖于支持向量，即使训练集里面所有非支持向量的点都被去除，重复训练过程，结果仍然会得到完全一样的模型。
一个 SVM 如果训练得出的支持向量个数比较少，那么SVM 训练出的模型比较容易被泛化。

参考：
原文链接：https://blog.csdn.net/qq_31347869/article/details/88071930

原文链接：https://blog.csdn.net/qq_31347869/article/details/88071930

原文链接：https://blog.csdn.net/lsb2002/article/details/131338700

小趴菜️

关注

43
点赞
踩
45

收藏

觉得还不错? 一键收藏
0
评论
机器学习6-支持向量机

SVM（支持向量机）是一种常见的监督学习算法，用于分类和回归问题。考虑一个二分类问题：假设输入空间与特征空间为两个不同的空间，这两个空间的元素一一对应，并将输入空间的输入映射为特征空间中的特征向量，支持向量机的学习是在特征空间进行的。在分类问题中，SVM通过在特征空间中找到一个最优的超平面来将不同类别的数据分隔开。在回归问题中，SVM通过寻找一个最优的超平面来拟合数据点，使得尽可能多的数据点位于超平面的边界上。
复制链接

扫一扫