详解SVM支持向量机算法(三:软间隔SVM和非线性SVM)

作者：RayChiu_Labloy
版权声明：著作权归作者所有，商业转载请联系作者获得授权，非商业转载请注明出处

---

目录

背景 

线性支持向量机(软间隔SVM)

硬间隔的问题 

引入松弛变量

目标函数的优化 

生成拉格朗日函数 

软间隔原始问题

软间隔对偶问题

求解思路：

对偶问题的求解

先求L函数对w，b，ξ的极小值

分析软间隔支持向量得出结论

总结软间隔SVM算法分析求解过程

设定惩罚系数C-构造优化问题

用SMO算法求出α*

计算W

找到全部的支持向量，计算出b

求b均值

非线性支持向量机

升维处理线性不可分

SVM的升维

维度爆炸和计算量问题

引入核函数取代计算非线性映射函数的内积

常用的核函数

核函数解决非线性分类的效果 

非线性SVM目标函数和求解过程总结

选择某个核函数及其对应的超参数

选择惩罚系数C

构造最优化问题

利用SMO算法求解出一组α*根据α*计算w* 根据α*找到全部支持向量，计算每个支持向量对应的bs*对bs*求均值得到最后的b*

---

背景 

        上一篇我们说到支持向量机分为三类：线性可分支持向量机(硬间隔SVM)、线性支持向量机(软间隔SVM)、非线性支持向量机,并且详细分析了硬间隔SVM得目标函数推导和求解，接下来继续说一下剩下得两个种类。

线性支持向量机(软间隔SVM)

硬间隔的问题 

         线性可分svm可通过构造超平面令硬间隔最大化，要正负例完美分开，从而求得最好的分隔超平面,实际情况的数据一半都不会太理想，总在或多或少的噪声数据，根据目标函数最优化我们无法找到一组w和b, 也就是我们就很难找到一个泛化能力很好的超平面了，即使找到了，也有可能是过拟合的。

 

引入松弛变量

        也就是说，硬间隔支持向量机要求所有的样本均被最佳超平面正确划分，要严格满足条件：，而软间隔支持向量机允许某些样本点不满足间隔大于等于1的条件。也就是说在上边这个约束条件上加了一个松弛变量ξi≥0（每个数据点自己有一个ξi）约束变成：

 

        这样就至少肯定有好多的w和b满足条件了 但是这相当于没有约束条件了，只要ξi无穷大，那么所有w和b都满足条件，ξ代表异常点嵌入间隔面的深度，我们要在能选出符合约束条件的最好的w和b的同时， 让嵌入间隔面的总深度越少越好

目标函数的优化 

生成拉格朗日函数 

        那么原来硬间隔的目标函数

        将会优化成这样：

        其实就是在原函数中引入一个惩罚系数 C>0，并对每个样本点引入一个松弛变量（slack variables）ξ≥0。

        再次根据f(x)和约束调试整理成拉格朗日函数：

        其中 αi≥0、 μi≥0是拉格朗日乘子。

软间隔原始问题

 

软间隔对偶问题

 

求解思路：

        先求L函数对w，b，ξ的极小值，再求其对α和μ的极大值

对偶问题的求解

先求L函数对w，b，ξ的极小值

        对3个参数w，b，ξ分别求偏导得

        带回拉格朗日函数

 

        整理约束条件

 

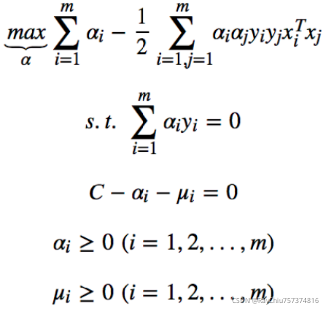
        发现基本式和硬间隔的一样，不过是约束条件变了。由于目标函数中并没有出现C，可将约束条件的第2，3，4项合并，消去C，得到最终的待优化函数为：

 

        与之前硬间隔相比，只是多了个约束条件而已，软间隔支持向量机对对偶变量的约束是 0≤αi≤C，硬间隔支持向量机对对偶变量的约束是 0≤αi，软间隔仍然可以使用 SMO来求解

分析软间隔支持向量得出结论

        •αi=0 -> 该点为分类正确的点

        •0<αi<C -> 该点为软边界上的点

        •αi=c -> 该点嵌入了软边界内

                • 此时如果ξ<1 ，该点被正确分类

                • 此时如果ξ=1 ，该点刚好落在超平面上

                • 此时如果ξ>1 , 该点被错误分类

总结软间隔SVM算法分析求解过程

设定惩罚系数C-构造优化问题

 

用SMO算法求出α*

计算W

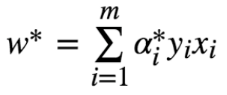
找到全部的支持向量，计算出b

 

求b均值

 

非线性支持向量机

升维处理线性不可分

 线性可分

 

 线性不可分

         不可分的数据通过一定方式升维到高维变成线性可分

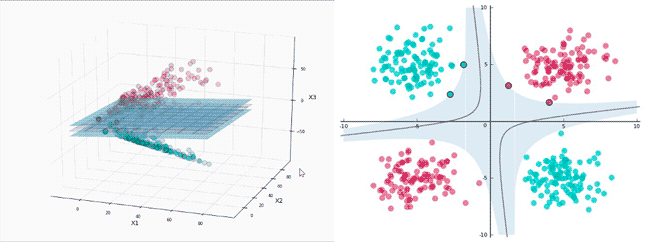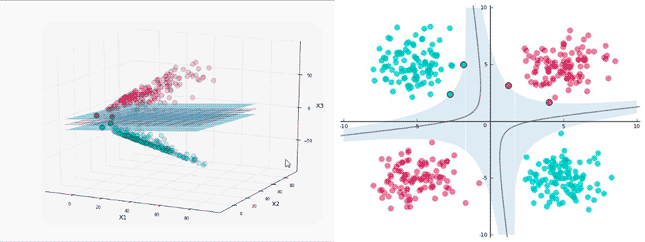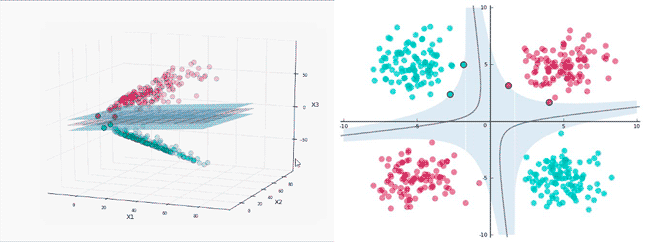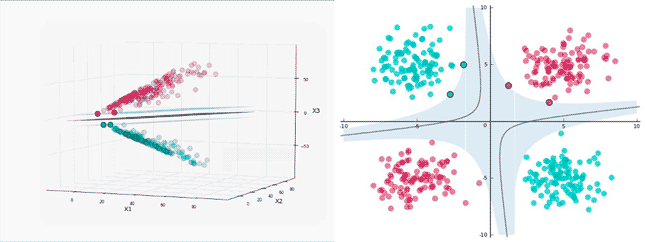
SVM的升维

        原始线性优化问题

     

        升维后：

维度爆炸和计算量问题

        升维有可能导致维度激增，例如使用多项式回归的方式进行升维，2维x1,x2会升到5维x1,x2,x1*x2,x1^2,x2^2，3维的升维会到19维，10维升维后会更夸张。

        而且升维后由于要计算即样本映射到特征空间之后的的内积，由于特征空间可能维度很高，甚至可能是无穷维，因此直接计算通常是很困难的

引入核函数取代计算非线性映射函数的内积

        由于优化问题中我们只需要求得的结果，并不需要知道具体的φ(x)是什么，于是为了解决该问题可设想存在核函数：

        这样跳过φ(x)直接定义的结果，既可以达到升维的效果，又可以避免维度爆炸的问题，这给求解带来很大的方便

         此时，对偶问题的目标函数变为了：

 

         判别函数(超平面f(x))变为了：

 

        补充一下之前的判别函数是这样： 又因为

 所以原来的判别式也可以写成这样：

常用的核函数

核函数解决非线性分类的效果 

        假设我们要建一个篱笆把羊群和狼群分开，这个篱笆就是分类器了，下边是SVM、逻辑回归、决策树分类的效果： 

 

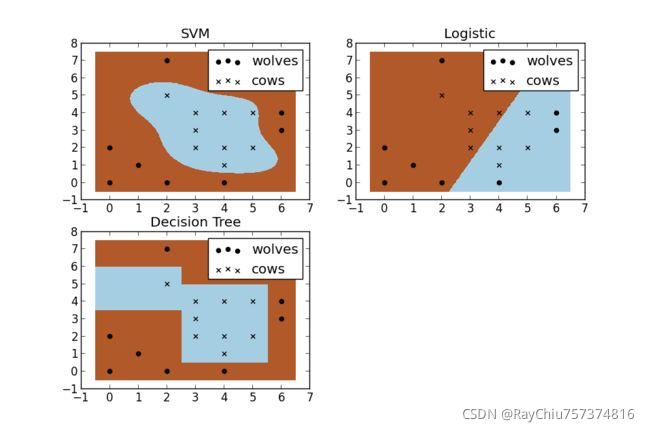
        可以看到SVM的效果是非常好的，从侧面简单说明了SVM使用非线性分类器的优势，而逻辑模式以及决策树模式都是使用了直线方法。 

非线性SVM目标函数和求解过程总结

选择某个核函数及其对应的超参数

选择惩罚系数C

构造最优化问题

 

利用SMO算法求解出一组α*
根据α*计算w* 
根据α*找到全部支持向量，计算每个支持向量对应的bs*
对bs*求均值得到最后的b*

        学得的超平面为：

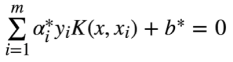
        最终的判别函数为： 

 

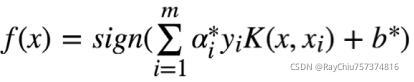
 参考：SVM_liugan528的博客-CSDN博客_svm

机器学习——svm支持向量机的原理 - it610.com

【如果对您有帮助，交个朋友给个一键三连吧，您的肯定是我博客高质量维护的动力！！！】