Coursera吴恩达《神经网络与深度学习》课程笔记（5）-- 深层神经网络

红色石头的个人网站：redstonewill.com

上节课我们主要介绍了浅层神经网络。首先介绍神经网络的基本结构，包括输入层，隐藏层和输出层。然后以简单的2 layer NN为例，详细推导了其正向传播过程和反向传播过程，使用梯度下降的方法优化神经网络参数。同时，我们还介绍了不同的激活函数，比较各自优缺点，讨论了激活函数必须是非线性的原因。最后介绍了神经网络参数随机初始化的必要性，特别是权重W，不同神经元的W不能初始化为同一零值。本节课是对上节课的延伸和扩展，讨论更深层的神经网络。

1. Deep L-layer neural network

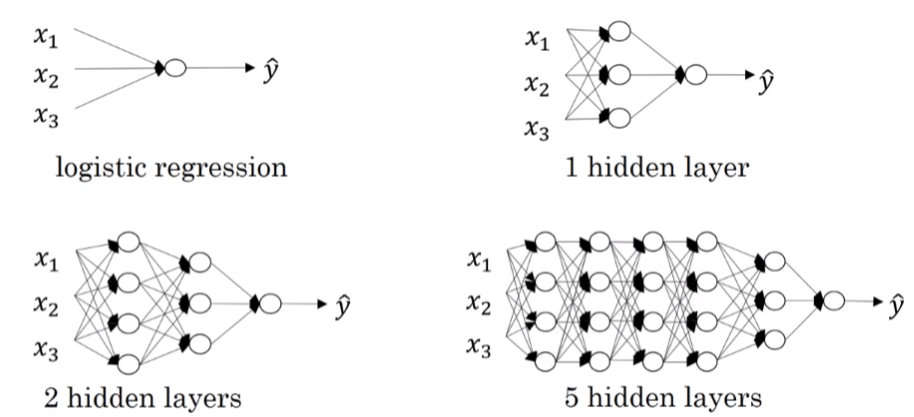
深层神经网络其实就是包含更多的隐藏层神经网络。如下图所示，分别列举了逻辑回归、1个隐藏层的神经网络、2个隐藏层的神经网络和5个隐藏层的神经网络它们的模型结构。

命名规则上，一般只参考隐藏层个数和输出层。例如，上图中的逻辑回归又叫1 layer NN，1个隐藏层的神经网络叫做2 layer NN，2个隐藏层的神经网络叫做3 layer NN，以此类推。如果是L-layer NN，则包含了L-1个隐藏层，最后的L层是输出层。

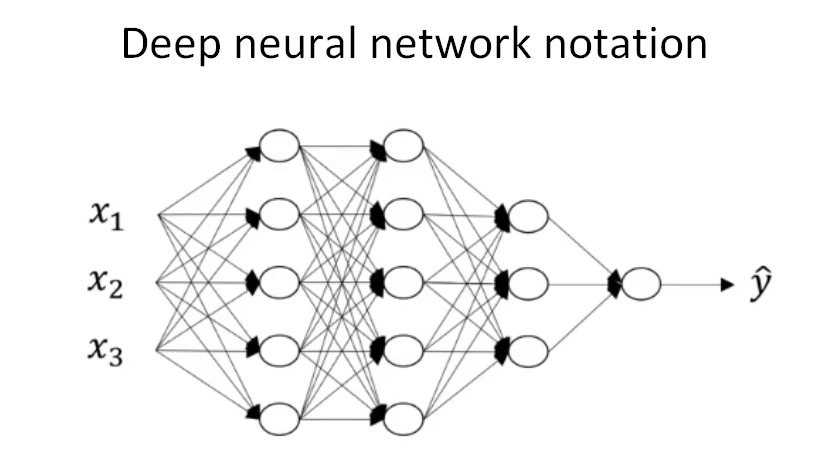
下面以一个4层神经网络为例来介绍关于神经网络的一些标记写法。如下图所示，首先，总层数用L表示，L=4。输入层是第0层，输出层是第L层。$n^{[l]}$表示第$l$层包含的单元个数，$l=0,1,\cdots,L$。这个模型中，$n^{[0]}=n_x=3$，表示三个输入特征$x_1,x_2,x_3$。$n^{[1]}=5$，$n^{[2]}=5$，$n^{[3]}=3$，$n^{[4]}=n^{[L]}=1$。第$l$层的激活函数输出用$a^{[l]}$表示，$a^{[l]}=g^{[l]}(z^{[l]})$。$W^{[l]}$表示第$l$层的权重，用于计算$z^{[l]}$。另外，我们把输入x记为$a^{[0]}$，把输出层$\hat y$记为$a^{[L]}$。

注意，$a^{[l]}$和$W^{[l]}$中的上标$l$都是从1开始的，$l=1,\cdots,L$。

2. Forward Propagation in a Deep Network

接下来，我们来推导一下深层神经网络的正向传播过程。仍以上面讲过的4层神经网络为例，对于单个样本：

第1层，$l=1$：

$$z^{[1]}=W^{[1]}x+b^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$$

$$a^{[1]}=g^{[1]}(z^{[1]})$$

第2层，$l=2$：

$$z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$$

$$a^{[2]}=g^{[2]}(z^{[2]})$$

第3层，$l=3$：

$$z^{[3]}=W^{[3]}a^{[2]}+b^{[3]}$$

$$a^{[3]}=g^{[3]}(z^{[3]})$$

第4层，$l=4$：

$$z^{[4]}=W^{[4]}a^{[3]}+b^{[4]}$$

$$a^{[4]}=g^{[4]}(z^{[4]})$$

如果有m个训练样本，其向量化矩阵形式为：

第1层，$l=1$：

$$Z^{[1]}=W^{[1]}X+b^{[1]}=W^{[1]}A^{[0]}+b^{[1]}$$

$$A^{[1]}=g^{[1]}(Z^{[1]})$$

第2层，$l=2$：

$$Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}$$

$$A^{[2]}=g^{[2]}(Z^{[2]})$$

第3层，$l=3$：

$$Z^{[3]}=W^{[3]}A^{[2]}+b^{[3]}$$

$$A^{[3]}=g^{[3]}(Z^{[3]})$$

第4层，$l=4$：

$$Z^{[4]}=W^{[4]}A^{[3]}+b^{[4]}$$

$$A^{[4]}=g^{[4]}(Z^{[4]})$$

综上所述，对于第$l$层，其正向传播过程的$Z^{[l]}$和$A^{[l]}$可以表示为：

$$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$$

$$A^{[l]}=g^{[l]}(Z^{[l]})$$

其中$l=1,\cdots,L$

3. Getting your matrix dimensions right

对于单个训练样本，输入x的维度是（$n^{[0]},1$）神经网络的参数$W^{[l]}$和$b^{[l]}$的维度分别是：

$$W^{[l]}:\ (n^{[l]},n^{[l-1]})$$

$$b^{[l]}:\ (n^{[l]},1)$$

其中，$l=1,\cdots,L$，$n^{[l]}$和$n^{[l-1]}$分别表示第$l$层和$l-1$层的所含单元个数。$n^{[0]}=n_x$，表示输入层特征数目。

顺便提一下，反向传播过程中的$dW^{[l]}$和$db^{[l]}$的维度分别是：

$$dW^{[l]}:\ (n^{[l]},n^{[l-1]})$$

$$db^{[l]}:\ (n^{[l]},1)$$

注意到，$W^{[l]}$与$dW^{[l]}$维度相同，$b^{[l]}$与$db^{[l]}$维度相同。这很容易理解。

正向传播过程中的$z^{[l]}$和$a^{[l]}$的维度分别是：

$$z^{[l]}:\ (n^{[l]},1)$$

$$a^{[l]}:\ (n^{[l]},1)$$

$z^{[l]}$和$a^{[l]}$的维度是一样的，且$dz^{[l]}$和$da^{[l]}$的维度均与$z^{[l]}$和$a^{[l]}$的维度一致。

对于m个训练样本，输入矩阵X的维度是（$n^{[0]},m$）。需要注意的是$W^{[l]}$和$b^{[l]}$的维度与只有单个样本是一致的：

$$W^{[l]}:\ (n^{[l]},n^{[l-1]})$$

$$b^{[l]}:\ (n^{[l]},1)$$

只不过在运算$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$中，$b^{[l]}$会被当成（$n^{[l]},m$）矩阵进行运算，这是因为python的广播性质，且$b^{[l]}$每一列向量都是一样的。$dW^{[l]}$和$db^{[l]}$的维度分别与$W^{[l]}$和$b^{[l]}$的相同。

但是，$Z^{[l]}$和$A^{[l]}$的维度发生了变化：

$$Z^{[l]}:\ (n^{[l]},m)$$

$$A^{[l]}:\ (n^{[l]},m)$$

$dZ^{[l]}$和$dA^{[l]}$的维度分别与$Z^{[l]}$和$A^{[l]}$的相同。

4. Why deep representations?

我们都知道神经网络能处理很多问题，而且效果显著。其强大能力主要源自神经网络足够“深”，也就是说网络层数越多，神经网络就更加复杂和深入，学习也更加准确。接下来，我们从几个例子入手，看一下为什么深度网络能够如此强大。

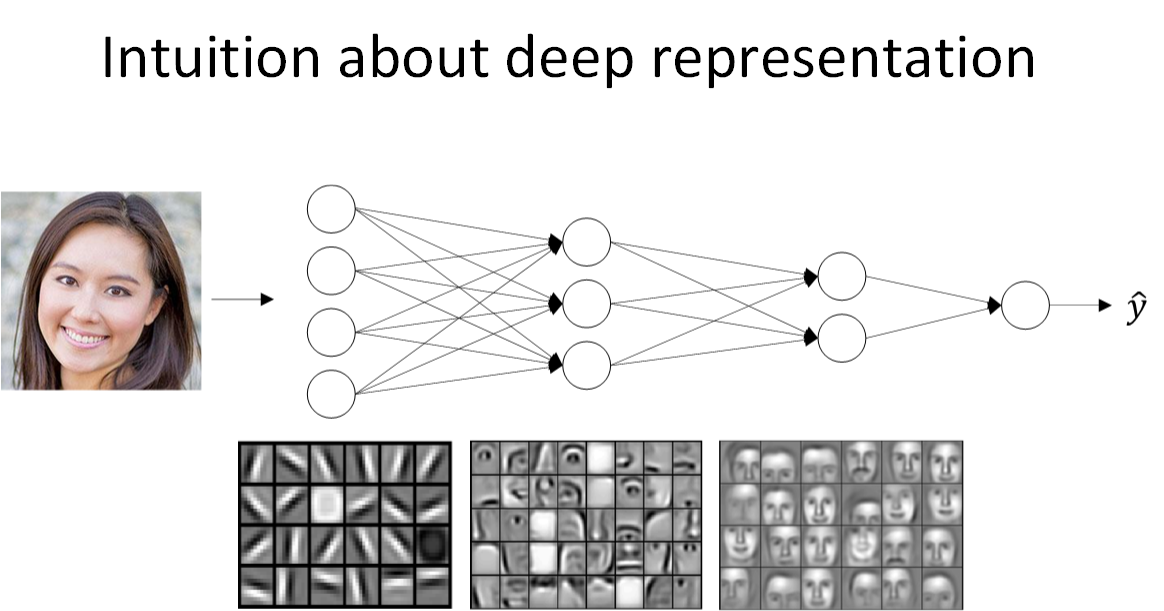
先来看人脸识别的例子，如下图所示。经过训练，神经网络第一层所做的事就是从原始图片中提取出人脸的轮廓与边缘，即边缘检测。这样每个神经元得到的是一些边缘信息。神经网络第二层所做的事情就是将前一层的边缘进行组合，组合成人脸一些局部特征，比如眼睛、鼻子、嘴巴等。再往后面，就将这些局部特征组合起来，融合成人脸的模样。可以看出，随着层数由浅到深，神经网络提取的特征也是从边缘到局部特征到整体，由简单到复杂。可见，如果隐藏层足够多，那么能够提取的特征就越丰富、越复杂，模型的准确率就会越高。

语音识别模型也是这个道理。浅层的神经元能够检测一些简单的音调，然后较深的神经元能够检测出基本的音素，更深的神经元就能够检测出单词信息。如果网络够深，还能对短语、句子进行检测。记住一点，神经网络从左到右，神经元提取的特征从简单到复杂。特征复杂度与神经网络层数成正相关。特征越来越复杂，功能也越来越强大。

除了从提取特征复杂度的角度来说明深层网络的优势之外，深层网络还有另外一个优点，就是能够减少神经元个数，从而减少计算量。例如下面这个例子，使用电路理论，计算逻辑输出：

$$y=x_1\oplus x_2\oplus x_3\oplus\cdots\oplus x_n$$

其中，$\oplus$表示异或操作。对于这个逻辑运算，如果使用深度网络，深度网络的结构是每层将前一层的两两单元进行异或，最后到一个输出，如下图左边所示。这样，整个深度网络的层数是$log_2(n)$，不包含输入层。总共使用的神经元个数为：

$$1+2+\cdots+2^{log_2(n)-1}=1\cdot\frac{1-2^{log_2(n)}}{1-2}=2^{log_2(n)}-1=n-1$$

可见，输入个数是n，这种深层网络所需的神经元个数仅仅是n-1个。

如果不用深层网络，仅仅使用单个隐藏层，那么需要的神经元个数将是指数级别那么大。Andrew指出，由于包含了所有的逻辑位（0和1），则需要$2^{n-1}$个神经元。这里笔者推导的是$2^n$个神经元，为啥是$2^{n-1}$请哪位高手解释下。

比较下来，处理同一逻辑问题，深层网络所需的神经元个数比浅层网络要少很多。这也是深层神经网络的优点之一。

尽管深度学习有着非常显著的优势，Andrew还是建议对实际问题进行建模时，尽量先选择层数少的神经网络模型，这也符合奥卡姆剃刀定律（Occam’s Razor）。对于比较复杂的问题，再使用较深的神经网络模型。

5. Building blocks of deep neural networks

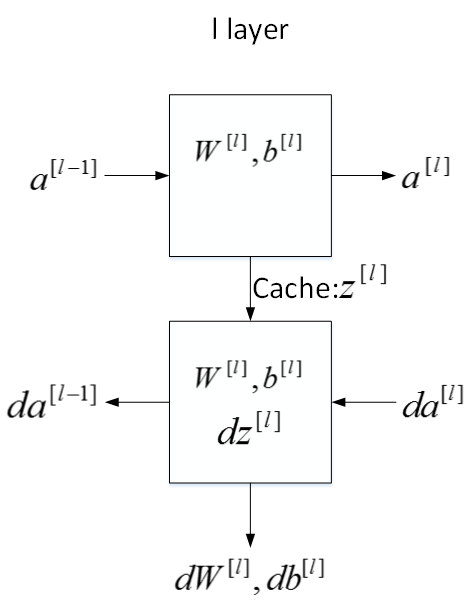
下面用流程块图来解释神经网络正向传播和反向传播过程。如下图所示，对于第$l$层来说，正向传播过程中：

输入：$a^{[l-1]}$

输出：$a^{[l]}$

参数：$W^{[l]},b^{[l]}$

缓存变量：$z^{[l]}$

反向传播过程中：

输入：$da^{[l]}$

输出：$da^{[l-1]},dW^{[l]},db^{[l]}$

参数：$W^{[l]},b^{[l]}$

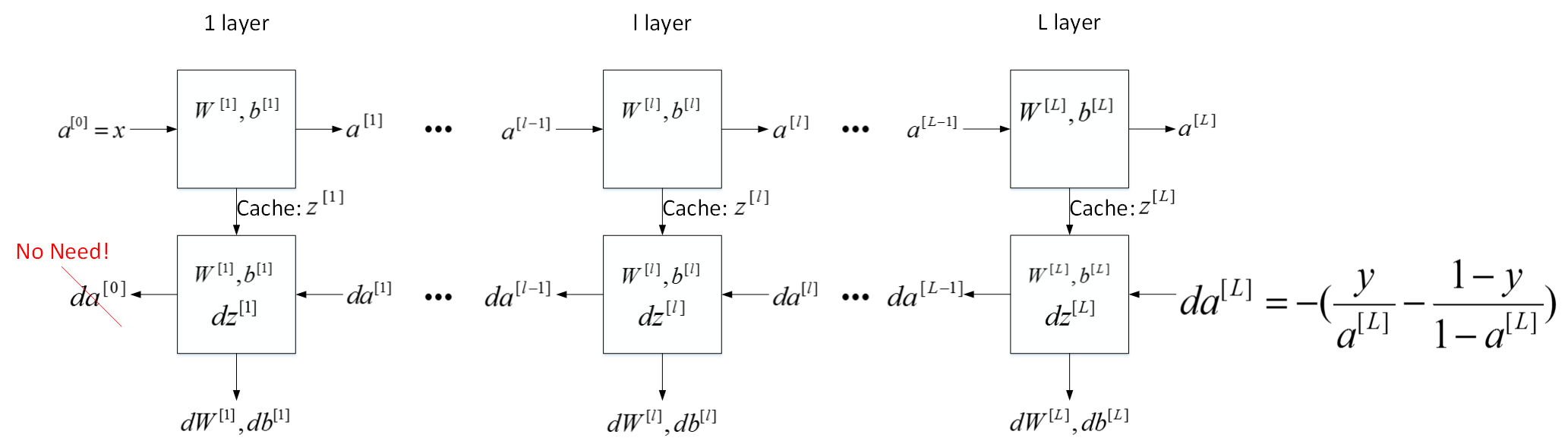
刚才这是第$l$层的流程块图，对于神经网络所有层，整体的流程块图正向传播过程和反向传播过程如下所示：

6. Forward and Backward Propagation

我们继续接着上一部分流程块图的内容，推导神经网络正向传播过程和反向传播过程的具体表达式。

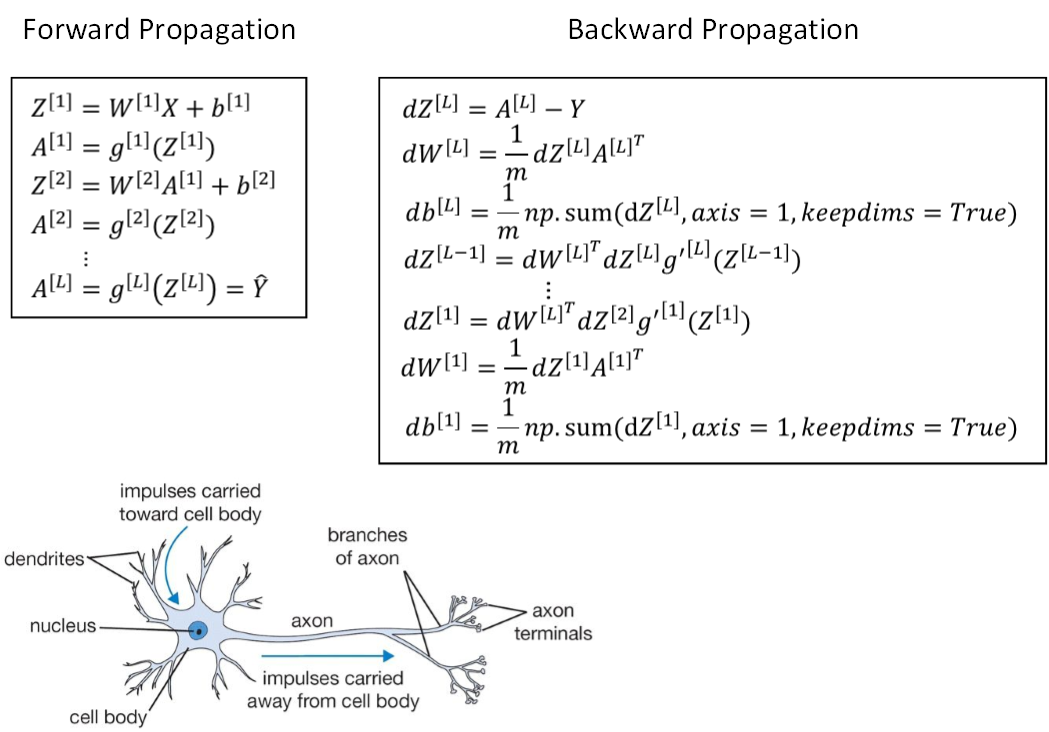
首先是正向传播过程，令层数为第$l$层，输入是$a^{[l-1]}$，输出是$a^{[l]}$，缓存变量是$z^{[l]}$。其表达式如下：

$$z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$$

$$a^{[l]}=g^{[l]}(z^{[l]})$$

m个训练样本，向量化形式为：

$$Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$$

$$A^{[l]}=g^{[l]}(Z^{[l]})$$

然后是反向传播过程，输入是$da^{[l]}$，输出是$da^{[l-1]},dw^{[l]},db^{[l]}$。其表达式如下：

$$dz^{[l]}=da^{[l]}\ast g^{[l]'}(z^{[l]})$$

$$dW^{[l]}=dz^{[l]}\cdot a^{[l-1]}$$

$$db^{[l]}=dz^{[l]}$$

$$da^{[l-1]}=W^{[l]T}\cdot dz^{[l]}$$

由上述第四个表达式可得$da^{[l]}=W^{[l+1]T}\cdot dz^{[l+1]}$，将$da^{[l]}$代入第一个表达式中可以得到：

$$dz^{[l]}=W^{[l+1]T}\cdot dz^{[l+1]}\ast g^{[l]'}(z^{[l]})$$

该式非常重要，反映了$dz^{[l+1]}$与$dz^{[l]}$的递推关系。

m个训练样本，向量化形式为：

$$dZ^{[l]}=dA^{[l]}\ast g^{[l]'}(Z^{[l]})$$

$$dW^{[l]}=\frac1mdZ^{[l]}\cdot A^{[l-1]T}$$

$$db^{[l]}=\frac1mnp.sum(dZ^{[l]},axis=1,keepdim=True)$$

$$dA^{[l-1]}=W^{[l]T}\cdot dZ^{[l]}$$

$$dZ^{[l]}=W^{[l+1]T}\cdot dZ^{[l+1]}\ast g^{[l]'}(Z^{[l]})$$

7. Parameters vs Hyperparameters

该部分介绍神经网络中的参数（parameters）和超参数（hyperparameters）的概念。

神经网络中的参数就是我们熟悉的$W^{[l]}$和$b^{[l]}$。而超参数则是例如学习速率$\alpha$，训练迭代次数N，神经网络层数L，各层神经元个数$n^{[l]}$，激活函数$g(z)$等。之所以叫做超参数的原因是它们决定了参数$W^{[l]}$和$b^{[l]}$的值。在后面的第二门课我们还将学习其它的超参数，这里先不讨论。

如何设置最优的超参数是一个比较困难的、需要经验知识的问题。通常的做法是选择超参数一定范围内的值，分别代入神经网络进行训练，测试cost function随着迭代次数增加的变化，根据结果选择cost function最小时对应的超参数值。这类似于validation的方法。

8. What does this have to do with the brain?

那么，神经网络跟人脑机制到底有什么联系呢？究竟有多少的相似程度？神经网络实际上可以分成两个部分：正向传播过程和反向传播过程。神经网络的每个神经元采用激活函数的方式，类似于感知机模型。这种模型与人脑神经元是类似的，可以说是一种非常简化的人脑神经元模型。如下图所示，人脑神经元可分为树突、细胞体、轴突三部分。树突接收外界电刺激信号（类比神经网络中神经元输入），传递给细胞体进行处理（类比神经网络中神经元激活函数运算），最后由轴突传递给下一个神经元（类比神经网络中神经元输出）。

值得一提的是，人脑神经元的结构和处理方式要复杂的多，神经网络模型只是非常简化的模型。人脑如何进行学习？是否也是通过反向传播和梯度下降算法现在还不清楚，可能会更加复杂。这是值得生物学家探索的事情。也许发现重要的新的人脑学习机制后，让我们的神经网络模型抛弃反向传播和梯度下降算法，能够实现更加准确和强大的神经网络模型！

9. Summary

本节课主要介绍了深层神经网络，是上一节浅层神经网络的拓展和归纳。首先，我们介绍了建立神经网络模型一些常用的标准的标记符号。然后，用流程块图的方式详细推导正向传播过程和反向传播过程的输入输出和参数表达式。我们也从提取特征复杂性和计算量的角度分别解释了深层神经网络为什么优于浅层神经网络。接着，我们介绍了超参数的概念，解释了超参数与参数的区别。最后，我们将神经网络与人脑做了类别，人工神经网络是简化的人脑模型。

至此，Andew深度学习专项课程第一门课《神经网络与深度学习》结束。

更多AI资源请关注公众号：红色石头的机器学习之路（ID：redstonewill）