看了别人的好多博客,感觉写的大部分都比较模糊,干脆自己写一份,总结一下,以后忘了可以看看。
树状数组在我们每个acmer入门的时候都是所必须要经历的一道门槛,做acm总是要经历很多东西,这个数组对于初学者确实比较难理解,其实我研究这个数组用了好几天才算研究好,但应该还没有到精通。
先来讲一下我们问什么来用树状数组:他的优点是代码短小,实现简单;容易扩展到高纬度的数据。但是他也有缺点,只能用于求和,不能求最大/小值,不能动态插入;数据多时,空间压力大。但是我是他觉得在求区间和上真的很方便的。
树状数组确实是个好东西啊,之前会套用模版,但确没有深入理解这个东西,先学会用轮子,然后再学造轮子嘛,这段时间再回头研究了一下,发现二进制在算法中真的是的好东西,它可以使算法的时间复杂度降到n的二进制表示中的1相关,大家都知道,求一个二进制中的1的个数,这个时间复杂度为O(logn)。
到底复杂在哪里? (博主也弄了很多时间在这上面)
有时候觉得树状数组难以理解,我觉得根本原因是:你还在用十进制的视角来看待树状数组,下面的讲解我会时刻提醒你转换到二进制的视角,而且我也不会先给你上图,因为你的视角在二进制,你就会发现树状数组就是一个普通的东西,不需要图你就能理解。
树状数组到底应该怎么用?(用处在哪些地方)(总的来说,修改和查询区间)
首先我们要构建好模型搞明白树状数组是用来干嘛的,现在有一个这样的问题:有一个数组a,下标从0到n-1,现在给你w次修改,q次查询,修改的话是修改数组中某一个元素的值;查询的话是查询数组中任意一个区间的和,w + q < 500000。
这个问题很常见,首先分析下朴素做法的时间复杂度,修改是O(1)的时间复杂度,而查询的话是O(n)的复杂度,总体时间复杂度为O(qn);可能你会想到前缀和来优化这个查询,我们也来分析下,查询的话是O(1)的复杂度,而修改的时候修改一个点,那么在之后的所有前缀和都要更新,所以修改的时间复杂度是O(n),总体时间复杂度还是O(qn)。
可以发现,两种做法中,要么查询是O(1),修改是O(n);要么修改是O(1),查询是O(n)。那么就有没有一种做法可以综合一下这两种朴素做法,然后整体时间复杂度可以降一个数量级呢?有的,对,就是树状数组。
(这段话引用他人博客)
不管三七二十一,先把模板搬上来再说,就算不理解也要会用轮子嘛!
模板:
int lowbit(int i)
{
return i & -i;//求数组下标数的二进制的非0最低位所表示的值
}
void add(int i,int t)//Add来更新数组;当数组元素有发生变化的时候,树状数组的优势非常的大
{
while(i<=n){
a[i]+=t;
i+=lowbit(i);//由叶子节点向上更新a数组
}
}
int Sum(int i)//Sum函数实际上就是把C数组全部加起来了
{
int sum=0;
while(i>0){
sum+=a[i];//从右往左区间求和
i-=lowbit(i);
}
return sum;
} 模板中最常见的三个函数。(单点更新,区间查询)。初学树状数组,来记录整理的笔记。树状数组,顾名思义是树状的数组。我们首先引入二叉树,叶子节点代表A[1]~A[8]。
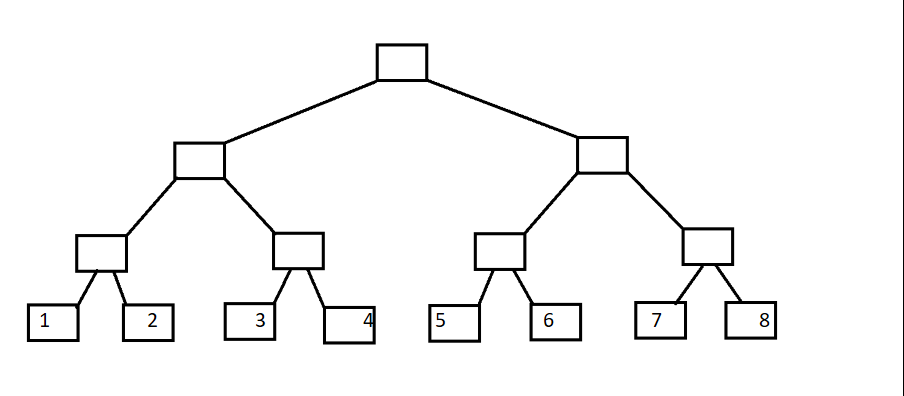
原来老套的数组a[1]~a[8]就是二叉树的叶子;
现在要对这颗二叉树进行变形:
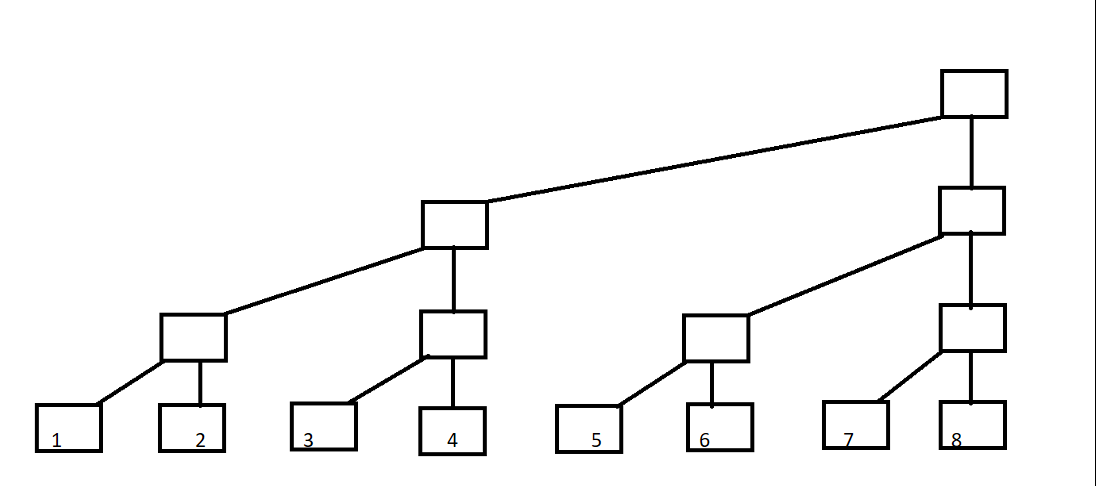
正式变形开始:
现在定义每一列的顶端节点c数组,如图:
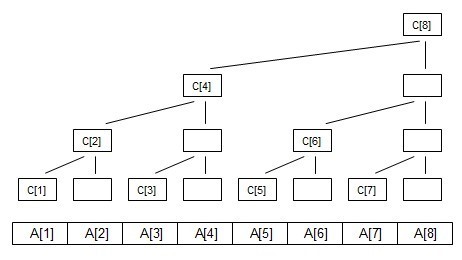
C[i]代表 子树的叶子结点的权值之和// 这里以求和举例
如图可以知道
C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
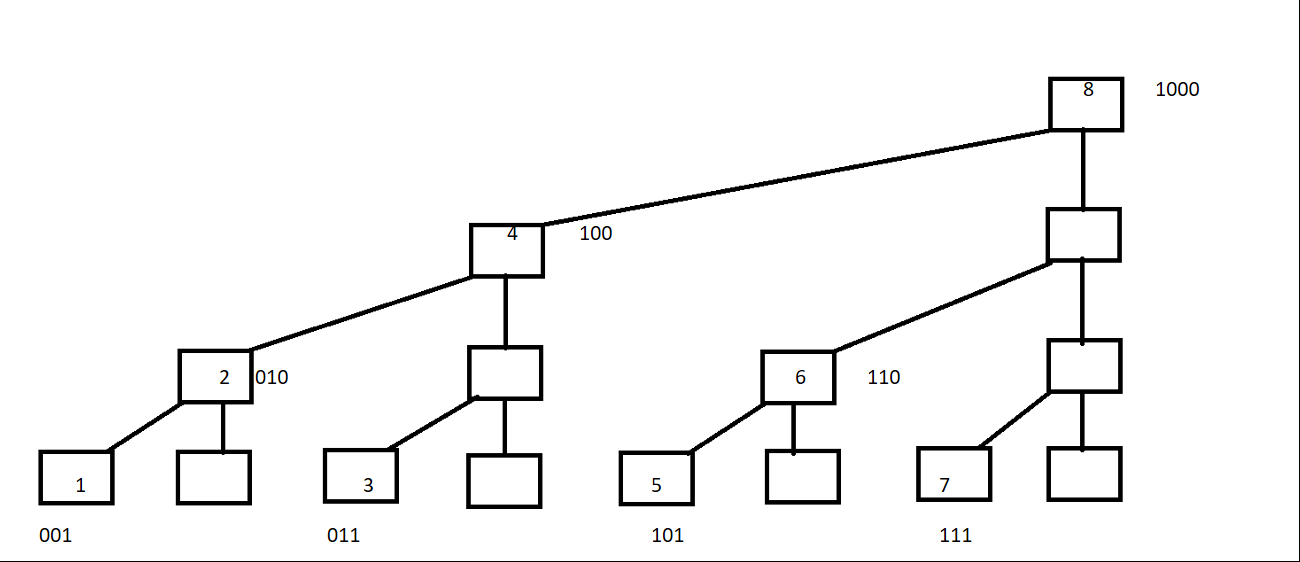
将C[i]数组的结点序号转化为二进制
1=(001) C[1]=A[1];
2=(010) C[2]=A[1]+A[2];
3=(011) C[3]=A[3];
4=(100) C[4]=A[1]+A[2]+A[3]+A[4];
5=(101) C[5]=A[5];
6=(110) C[6]=A[5]+A[6];
7=(111) C[7]=A[7];
8=(1000) C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
对照式子可以发现 C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; (k为i的二进制中从最低位到高位连续零的长度)例如i=8时,k=3;
可以自行带入验证;现在引入lowbit(x) lowbit(x) 其实就是取出x的最低位1 换言之 lowbit(x)=2^k k的含义与上面相同 理解一下
int lowbit(int t)
{
return t&(-t);
}
/*
-t 代表t的负数 计算机中负数使用对应的正数的补码来表示
例如 : t=6(0110) 此时 k=1
-t=-6=(1001+1)=(1010)
t&(-t)=(0010)=2=2^1
C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i];
C[i]=A[i-lowbit(i)+1]+A[i-lowbit(i)+2]+......A[i];
*/区间查询:
下面利用C[i]数组,求A数组中前i项的和
举个栗子: i=7;
前i项和:sum[7]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7] ;
C[4]=A[1]+A[2]+A[3]+A[4]; C[6]=A[5]+A[6]; C[7]=A[7];
可以推出: sum[7]=C[4]+C[6]+C[7];
序号写为二进制: sum[(111)]=C[(100)]+C[(110)]+C[(111)];
再举个栗子: i=5;
前i项和:sum[5]=A[1]+A[2]+A[3]+A[4]+A[5] ;
C[4]=A[1]+A[2]+A[3]+A[4]; C[5]=A[5];
可以推出: sum[5]=C[4]+C[5];
序号写为二进制: sum[(101)]=C[(100)]+C[(101)];
细细观察二进制 树状数组追其根本就是二进制的应用
结合代码演示一下代码过程:
int sum(int i)//求和节点的值
{
int ret=0;
while(i>0){
ret+=a[i];//从右往左区间求和
i-=lowbit(i);
}
return ret;
}对于i=7 进行演示:
7(111) ans+=C[7]
lowbit(7)=001 7-lowbit(7)=6(110) ans+=C[6]
lowbit(6)=010 6-lowbit(6)=4(100) ans+=C[4]
lowbit(4)=100 4-lowbit(4)=0(000)
对于i=5 进行演示 :
5(101) ans+=C[5]
lowbit(5)=001 5-lowbit(5)=4(100) ans+=C[4]
lowbit(4)=100 4-lowbit(4)=0(000)
单点更新:当我们修改A[]数组中的某一个值时 应当如何更新C[]数组呢?
回想一下 区间查询的过程,再看一下上文中列出的图。
void update(int i,int val)//更新单节点的值
{
while(i<=n){
a[i]+=val;
i+=lowbit(i);//由叶子节点向上更新a数组
}
}
//可以发现 更新过程是查询过程的逆过程
//由叶子结点向上更新C[]数组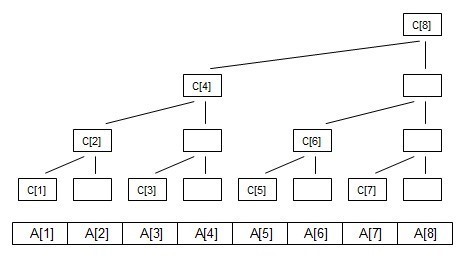
如图: 当更新A[1]时 需要向上更新C[1] ,C[2],C[4],C[8]
C[1], C[2], C[4], C[8]
写为二进制 C[(001)],C[(010)],C[(100)],C[(1000)]
1(001) C[1]+=A[1]
lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]
————————————————————————————————————————————————————————
再引用另外一篇博主的文章:我觉得还是可以的;
树状数组的思想
在树状数组的问题模型中已经有所提及了,就是那两种不同做法的一个综合;
先定义一些东西:arr是原数组,c是新开的一个数组,这个数组代表后缀和(问题模型中是用的前缀和,这里要用后缀和,具体原因马上就知道了);
二进制的视角:一个数n,假设n = 6,它的二进制为110,我们把它表示成累加的形式110 = 100 + 10,这样是可以的,那么我们要求前6(110)项的和是不是可以这样求:
∑i=16=(arr1+arr2+arr3+arr4)+(arr5+arr6)∑i=16=(arr1+arr2+arr3+arr4)+(arr5+arr6)
注意括号中的元素个数,是不是4(100)个加2(10)个,和110 = 100 + 10是不是很像,不知你们发现了吗,10就是lowbit(110)的结果,100是lowbit(100)的结果。求和的时候我们总是把∑ni=1∑i=1n拆分成这样的几段区间和来计算,而如何去确定这些区间的起点和长度呢?就是根据n的二进制来的(不懂的可以再看下上面举的例子),二进制怎么拆的,你就怎么拆分,而拆分二进制就要用到上面说的lowbit函数了。这里也可以顺理成章得给出c数组的表示了。
这里也可以顺理成章得给出c数组的表示了,c[i]表示从第i个元素向前数lowbit(i)个元素,这一段的和,这就是上面说的区间和,只不过这个区间是靠右端点的;你可能又会想,不是说区间是靠右端点的吗,是后缀和啊,那中间的这些区间怎么定义?其实递归定义就好了,比如说∑6i=1=(arr1+arr2+arr3+arr4)+(arr5+arr6)=∑6i=1=(arr1+arr2+arr3+arr4)+c[6]∑i=16=(arr1+arr2+arr3+arr4)+(arr5+arr6)=∑i=16=(arr1+arr2+arr3+arr4)+c[6],你把c[6]去掉,不就是∑4i=1=(arr1+arr2+arr3+arr4)∑i=14=(arr1+arr2+arr3+arr4),这个区间不就靠右端点了吗,∑4i=1=c[4]=c[6−lowbit(6)]∑i=14=c[4]=c[6−lowbit(6)]。
其实你把所有的数字都看成二进
树状数组的实现
设计一种数据结构,需要的操作无非就是”增删改查“,这里只讨论查询和修改操作具体是怎么实现的;
查询
这里说的查询是查询任一区间的和,由于区间和具有可加减性,故转化为求前缀和;
查询前缀和刚刚在树状数组的思想中已经说过了,就是把大区间分成几段长度不等的小区间,然后求和。区间的个数为O(logn)O(logn),所以查询的时间复杂度为O(logn)O(logn)。
修改
修改某一位置上的元素的时间复杂度为O(1)O(1),但是要更新c数组,不然查询的时间复杂度就会变高。更新的方法就要提一下树状数组的性质了和树状数组那张经典的图片了。
制,很好理解的。
这张图片中已经把c数组的后缀和这个含义已经表达得很清楚了。这个时候你再把查询操作对应到这张图上,然后看着二进制来操作,是不是就可以很直白地理解上面所说的查询操作了!
我们从这张图中可以得到树状数组的如下性质:
- 后缀和的长度是2的幂;
- 上一层后缀和的长度是下一层后缀和长度的两倍;
- 下一层后缀和只要补上自己后缀和的长度就可以得到上面层的后缀和(图中的虚框框),注意,是上面的后缀和,而不是上一层的后缀和,这个性质就是更新操作的依据;
- 最后一位
1右边有多少个0(可以用log2(lowbit(x))log2(lowbit(x))表示)就表示这一层有多少个直系子层(子层的意思就是这一层的和包含下面某一层的和)。
我暂时就写这么多吧,这个时候我们再来说更新操作;
更新的时候只要更新修改这个点会影响到的那些后缀和(c数组),假设现在修改6(110)这个点,依据树状数组的性质三,它影响的直系父层就是c[6(110) + lowbit(6(110))] = c[8(1000)],但是它肯定不是只影响直系父层,上面所有包含这一层和的层都要更新,但是我们把这个更新传递给直系父层c[8],8这个点的直系父层是c[16],依次类推地更新就行了。
关于对树状数组的研究本博客将持续进行更新,欢迎大家关注!
如果还有不懂的可以参考题目:
https://blog.csdn.net/rnzhiw/article/details/81137554,
https://blog.csdn.net/rnzhiw/article/details/81289584








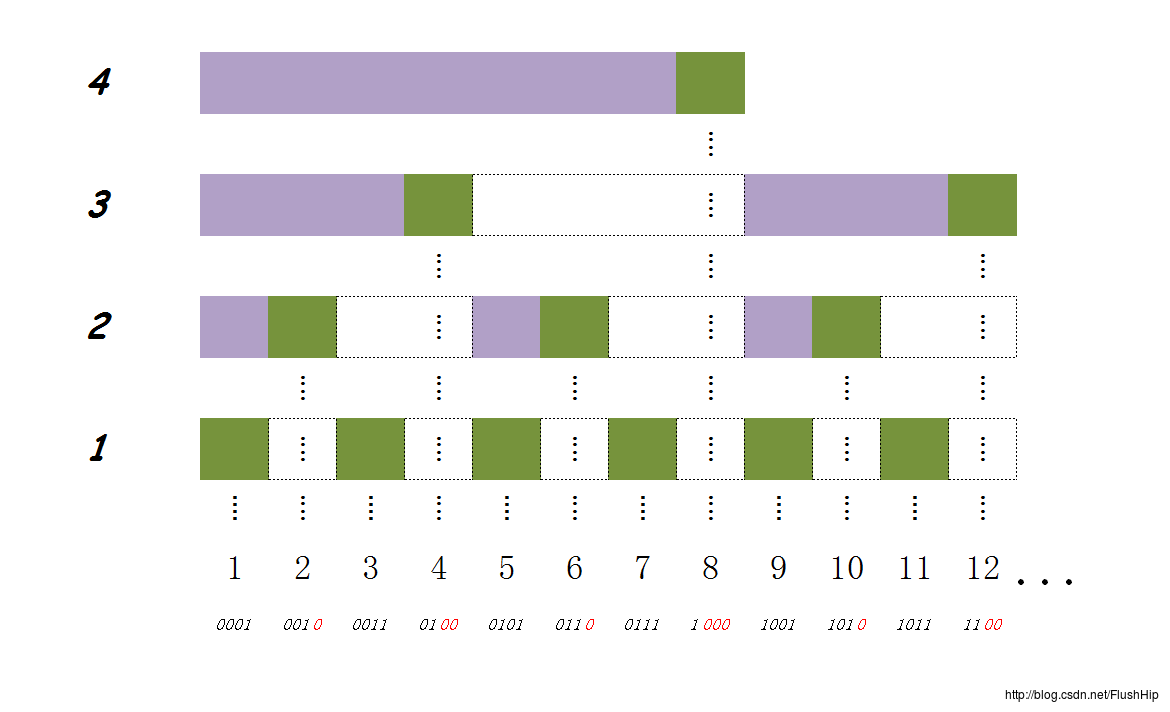














 232
232











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








