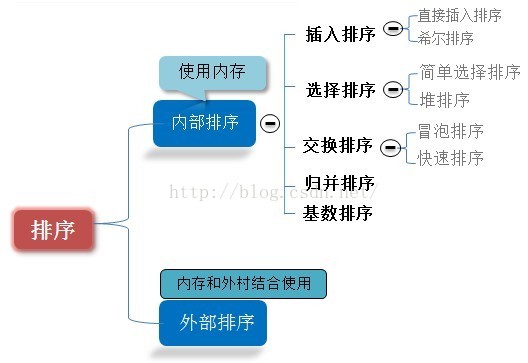
本文给出了八大排序算法的简单思路介绍以及代码实现(仅核心代码,程序中出现的drive函数为排序驱动程序)。
1. 插入排序
1)将一个元素插入到已经排好序的有序表中,从而使得有序表的个数+1。 算法从第二个元素开始。将一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。
2) 从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置以使得其变成有序的序列。(如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。)
void insertSort(int* a, int n)
{
int i, j, temp;
for( i = 1; i < n; i++ )
{
temp = a[i];
for( j = i - 1; j >= 0 && temp < a[j]; j-- )
a[j + 1] = a[j];
a[j + 1] = temp;
}
}冒泡排序(Bubble Sort)也是一种简单直观的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。也就是说在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
void bubbleSort(int* a, int size)
{
int i, j, temp;
for( i = 0; i < size - 1; i++ )
{
for( j = 0; j < size - i - 1; j++ )
{
if( a[j + 1] < a[j] )
{
temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
}
}1)首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置
2)再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
3)重复第二步,直到所有元素均排序完毕。
void selectionSort(int* a, int size)
{
int min_index, min_value, i, j, temp;
for( i = 0; i < size - 1; i++ )
{
min_index = i;
min_value = a[i];
for( j = i + 1; j < size; j++ )
{
if( min_value > a[j] )
{
min_value = a[j];
min_index = j;
}
}
if( i != min_index )
{
temp = a[i];
a[i] = a[min_index];
a[min_index] = temp;
}
}
}4.快速排序
快速排序是在实践中最快的已知的排序算法,他的平均运行时间是O(NlogN),该算法之所以非常的快是因为非常精炼和高度优化的内部循环。它的最坏的情形的性能是O(N^2),但是只要稍加努力就可以改变这个情况。 像归并算法一样,快速排序算法也是一种分治的递归算法,将数组S排序的基本算法是由以下简单的4步组成:
1. 如果S中的元素个数为0, 1, 则返回
2. 取S中的任一元素v, 称之为枢纽元(pivot)。
3. 将其余的元素分成两个不相交的集合,S1和S2。
4. 返回quickSort(S1), 继随v, 继而quickSort(S2)
快速排序更快的原因在于第3步分割成两组实际上是在适当的位置进行并且非常的有效, 它的高效性弥补了将一个大问题分为两个可能大小不等的子问题的缺陷。实现2和3步有许多的方法,这里介绍的方法是大量的分析和经验研究的结果。
1, 选择枢纽元。无论选择哪里元素作为枢纽元都可以完成排序工作,但是有些选择明显是更优的。
1)一种错误的方法:
将第一个元素作为pivot, 如果输入的待排序的data是无序的,则这么做是可以的接受的,但是如果输入是预排序, 那么这样做就会产生一个劣质的分割。
2)一种安全的做法:
一种安全的方针是随机的选取pivot, 一般来说这种策略是非常安全的, 但是另一方面值得指出的是, 随机数的生成是非常昂贵的, 根本减少不了算法的其他方面的运行时间。
3)三数中值分割法:
pivot的最好的选择是待排序数组的中值,不幸的是,这是很难算出的。这样的中值的估计量可以通过随机选取3个元素并且使用它们的中值为作为pivot而得到。一般的做法是使用左端,右端和中间位置上的3个元素得到。
算法过程的简单描述: 首先使用上述的三数中值分割法产生枢纽元, 将该枢纽元与最后一个元素互换位置(脱离待排序的序列)。然后使得iptr指向第一个元素, jptr指向倒数第二个元素。比较data[i]与pivot,若data[i]<pivot则说明,data[i]位置正确(小元素应该在左半部分),i++继续比较直到data[i]>pivot,说明此时的data[i]位置不对,data[i]属于大元素,应该在右边部分, 故互换data[i]与data[j]。 此时data[j]找到了自己的正确的位置, j--。若data[j]>pviot, 则继续往左走,直到data[j]<pivot, 说明此时data[j]的位置不对,data[j]属于小元素,应该位于左半部分。交换data[i]与data[j]的位置。整个过程直到i==j停止。
改进的算法过程的描述:主要的区别在于,每一轮交换之前,首先iptr从左向右扫描属于大元素(属于左部分)的项,找到之后不马上交换,而是jptr从右向左扫描属于小元素(属于右边部分)的项,然后交换。
int median3(int start, int end)
{
int center = (start + end) / 2;
if( data[start] > data[center] )
swap(start, center);
if( data[start] > data[end] )
swap(start, end);
if( data[center] > data[end] )
swap(center, end);
swap(center, end - 1);
return data[center];
}
void quickSort(int* a, int start, int end)
{
int iptr, jptr;
iptr = start;
jptr = end - 1;
int pivot = median3(start, end);
if( 8 <= end - start )
{
for( ; ; )
{
while( a[++iptr] < pivot );
while( a[--jptr] > pivot );
if( iptr < jptr )
swap(iptr, jptr);
else
break;
}
swap(iptr, end - 1);
quickSort(a, start, iptr - 1);
quickSort(a, iptr + 1, end);
}
else
insertSort(a, start, end);
}
void insertSort(int* a, int start, int end)
{
int i, j, temp;
for( i = 1; i < end; i++ )
{
temp = a[i];
for( j = i - 1; j >= 0 && a[j] > temp; j-- )
a[j + 1] = a[j];
a[j + 1] = temp;
}
}
void swap(int i, int j)
{
int temp;
temp = data[i];
data[i] = data[j];
data[j] = temp;
}
void drive(int* a, int number)
{
int i;
quickSort(data, 0, number - 1);
}5.归并排序
归并排序以O(NlogN)最坏情况运行时间运行,这个算法的基本操作是合并两个已经排序好的表, 因此, 归并排序是很好描述的,如果N = 1, 那么只有一个元素需要排序, 答案是显然的,否则, 递归的将前半部分数据和后半部分数据进行归并排序,将排序得到的两部分的数据使用合并算法合在一起。该算法是经典的分治策略。
void mergeSort(int* a, int* temp, int start, int end)
{
int center;
if( start < end )
{
center = (start + end) / 2;
mergeSort(a, temp, start, center);
mergeSort(a, temp, center + 1, end);
merge(a, temp, start, center, end);
}
}
void merge(int* a, int* temp, int left, int center, int right)
{
int Aptr, Bptr, Cptr;
Aptr = Cptr = left;
Bptr = center + 1;
int i;
while( Aptr <= center && Bptr <= right )
if( a[Aptr] < a[Bptr] )
temp[Cptr++] = a[Aptr++];
else
temp[Cptr++] = a[Bptr++];
while( Aptr <= center )
temp[Cptr++] = a[Aptr++];
while( Bptr <= right )
temp[Cptr++] = a[Bptr++];
for( i = left; i <= right; i++ )
data[i] = temp[i];
}
void drive(int number)
{
int* temp;
int i;
if( !(temp = (int*)malloc(sizeof(int) * number)))
{
printf("temp malloc error");
exit(0);
}
mergeSort(data, temp, 0, number - 1);
}6.希尔排序
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本,但希尔排序是非稳定排序算法。希尔排序是基于插入排序的以下两点性质而提出改进方法的:
1.插入排序在对几乎已经排好序的数据操作时, 效率高, 即可以达到线性排序的效率。
2.但插入排序一般来说是低效的, 因为插入排序每次只能将数据移动一位
希尔排序的基本思想是:先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
算法步骤:
1)选择一个增量序列t1,t2,…,tk,其中ti>tj,tk=1;
2)按增量序列个数k,对序列进行k 趟排序;
3)每趟排序,根据对应的增量ti,将待排序列分割成若干长度为m 的子序列,分
别对各子表进行直接插入排序。仅增量因子为1 时,整个序列作为一个表来处
理,表长度即为整个序列的长度。
void shellInsertSort(int* a, int size)
{
int i, j, increment, temp;
for( increment = size / 2; increment > 0; increment /= 2 )
{
for( i = increment; i < size; i++ )
{
temp = a[i];
for( j = i - increment; j >= 0; j -= increment )
{
if( temp < a[j] )
a[j + increment] = a[j];
else
break;
}
a[j + increment] = temp;
}
}
}7.堆排序
堆排序是基于数据结构大顶堆。
1、建立一个大顶堆:在数组中从的size/2 - 1开始进行调整。使之成为大顶堆。
2、开始进行堆排序:将根元素和当前堆的最后一个元素(因为当前的堆是在不断的缩小的)互换, 这样,大顶堆的结构遭到了破坏,使用调整函数进行调整。持续这个过程直到堆中只剩下一个元素。此时,该数组排序完成。
void adjustDown(int* a, int i, int size)
{
int temp, child;
for( temp = a[i]; leftchild(i) < size; ) //保留待调整的元素为temp,接下来
//就是要为temp找到合适的位置
{
child = leftchild(i);
if( child != size - 1 && a[child] < a[child + 1] )
child++; //获得应该上调的孩子的位置
if( temp < a[child] )
a[i] = a[child]; //如果temp小于其中的一个孩子则上调
else
break; //如果temp比两个孩子都大,调整完毕, 大顶堆的结构恢复
i = child; //开始调整以“大”孩子为根的大顶堆
}
a[i] = temp;
}
void heapSort(int* a, int size)
{
int i;
for( i = size / 2 - 1; i >= 0; i-- )
adjustDown(a, i, size);
for( i = size - 1; i > 0; i-- )
{
swap(a, 0, i);
adjustDown(a, 0, i);
}
}
void swap(int* a, int i, int j)
{
int temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}






















 903
903

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








