Kernel Logistic Regression(带核函数的逻辑斯蒂回归)
本篇要介绍的是将Logistic Regression和Kernel函数结合在一起的应用。即我们要讨论的是:如果想要把 Kernel K e r n e l 的技巧使用在 logistic Regression l o g i s t i c R e g r e s s i o n 上,我们应该怎么做?
- SVM学习笔记-线性支撑向量机
- SVM学习笔记-对偶形式的SVM
- SVM学习笔记-核函数与非线性SVM
- SVM学习笔记-软间隔SVM
- Kernel Logistic Regression
- Support Vector Regression(SVR)
1 - Soft-Margin SVM as Regularized Model
1.1 - SVM及核模型
硬间隔SVM的原始形式(hard margin primal):想要找一个能正确划分数据的最“胖”的边界,经过一些转换推导得到下面的问题。
硬间隔SVM的对偶形式(hard margin dual):将原始问题转化为对偶问题。对偶问题的特点是:和经过特征转换之后的
Z
Z
空间的维度没有任何的关系,只和样本的数量有关系。当然要和空间的维度完全没有关系还需要使用核技巧。
软间隔的原始问题(soft margin primal):从硬间隔出发,不再要求所有的数据点都需要被正确的划分,即允许有一些误分的数据点,然后对这些误分的数据点“犯的错”进行惩罚而得到了软间隔分类器,这样可以对噪声有一定的容忍度。
软间隔的对偶问题(soft margin dual):和硬间隔的对偶问题几乎是一致的,唯一不同的地方就是
αn
α
n
有上限
C
C
。引入是为了平衡间隔的大小和对错误的容忍度。
soft
s
o
f
t
-
margin
m
a
r
g
i
n
是实务上比较常用的
SVM
S
V
M
。
1.2 - 松弛变量slack variables
在软间隔的 SVM S V M 中,我们使用变量 ξn ξ n 来记录每一个数据点距离间隔边界(不是间隔,是间隔边界)的大小 margin m a r g i n - violation v i o l a t i o n 。并且在目标函数中对所有的 margin m a r g i n - violation v i o l a t i o n 做出惩罚,使其和最小化。
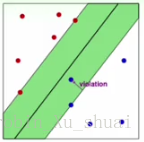
对于任意一条分隔边界 w,b w , b ,我们考虑一下 ξ ξ 是怎么计算出来的:
- 如果某一个点 (xn.yn) ( x n . y n ) 被划分错误,即 yn(wTxn+b)<1 y n ( w T x n + b ) < 1 , 此时 ξn ξ n 可以记录下这个点不满足条件的程度。 margin violation m a r g i n v i o l a t i o n 为 ξn=1−yn(wTxn+b)>0 ξ n = 1 − y n ( w T x n + b ) > 0 ;
- 如果某一个点 (xn,yn) ( x n , y n ) 划分正确, 即 yn(wTxn+b)≥1 y n ( w T x n + b ) ≥ 1 ,那么 ξn=0 ξ n = 0 。
所以对于任意的
w,b
w
,
b
,某一个点
(xn,yn)
(
x
n
,
y
n
)
的
ξn
ξ
n
的计算公式简化如下:
即, 如果 (xn.yn) ( x n . y n ) 符合约束, max m a x 中的前一项小于0,结果为0;如果该点不符合约束, max m a x 中的前一项大于0,这样就记录了违反的大小。
所以我们的 soft margin SVM s o f t m a r g i n S V M 可以写成下面的无约束形式:
对于上面的这种形式,只需要调 w w ,的值使得总体最小化就好了
发现上面的式子似曾相识,上面的式子可以简单的写成:
其中的 12wTw 1 2 w T w 可以看做是 regularizer r e g u l a r i z e r ,所以 soft margin SVM s o f t m a r g i n S V M 可以看成是一种加了 regularizer r e g u l a r i z e r 的最优化问题,但是这个问题有两个缺陷:
- 首先这不是一个二次规划问题,所以没有办法使用核技巧。
- max(⋅,0) m a x ( ⋅ , 0 ) 不是可微分的,所以很难去求解。
所以并没有从这个角度出发去讲解 soft margin SVM s o f t m a r g i n S V M ,而是一步一步的从 hard margin SVM h a r d m a r g i n S V M 演化过来。
1.3 - 比较两个问题
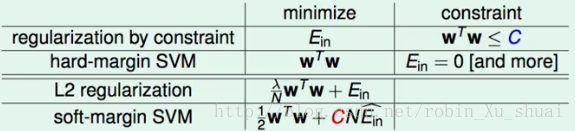
之前我们提到过, hard margin SVM h a r d m a r g i n S V M 和 regularization r e g u l a r i z a t i o n 是很相似的。 regularization r e g u l a r i z a t i o n 中最小化 Ein E i n 的同时在 w w 上添加条件;在 Ein E i n 上添加更严格的条件同时最小化 w w 。如表格中的前两行所示。
- L2 regularization:
- soft-margin SVM:
12wTw+CEin 1 2 w T w + C E i n SVM S V M 中的 large margin l a r g e m a r g i n 可以看做是 L2 regularization L 2 r e g u l a r i z a t i o n 的一种实现。因为有 large margin l a r g e m a r g i n 的要求,所以会限制 hyperplanes h y p e r p l a n e s 的个数,这可以理解为一种 regularizer r e g u l a r i z e r 。
在最初的 regularization r e g u l a r i z a t i o n 问题中:我们想要最小化 Ein E i n ,但是不想过分的最小化 Ein E i n ,所以添加了一个限制条件 wTw≤ w T w ≤ C C 。在中,也有一个参数 C C ,用来决定惩罚的力度有多大。在问题中有一个参数 λ λ , C C 和的作用相同, 其值越大,对应于 λ λ 的值越小,此时表明只是想要一点点的正则化; C C 和值越小, 对应于 λ λ 的值越大,表明想要更多的正则化。
2 - SVM versus Logistic Regression
2.1 - 损失函数
上一小节中将 soft margin SVM s o f t m a r g i n S V M 写成了另一种形式, 在这种形式里面 soft margin SVM s o f t m a r g i n S V M 是要最小化两项的和,其中的一项是 ∑err ∑ e r r 。 其中的 err=max(1−y×分数, 0) e r r = m a x ( 1 − y × 分 数 , 0 ) 。
我们现在来比较下这个 err e r r 和我们在二元分类中关心的 err0/1 e r r 0 / 1 有什么关系。s=wTzn+b s = w T z n + b
- err0/1(s,y)=|[ys≤0]| e r r 0 / 1 ( s , y ) = | [ y s ≤ 0 ] |
- errsvm(s,y)=max(1−ys,0) e r r s v m ( s , y ) = m a x ( 1 − y s , 0 ) 是 err0/1 e r r 0 / 1 的上界
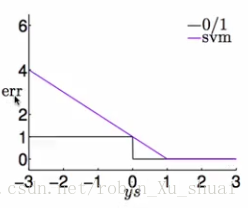
将上述的两个 err e r r 函数分别画在下图中, err0/1 e r r 0 / 1 是比较容易画出来的:当 y y 和分数同号的时候 err e r r 为 0 0 ,当和分数 s s 不同号的时候为 1 1 ;对于分成两个部分画:有 violation v i o l a t i o n 的时候,即 y∗s<1 y ∗ s < 1 ,这个时候 err e r r 的值为 1−y∗s 1 − y ∗ s ;没有 violation v i o l a t i o n 的时候,即 y∗s≥1 y ∗ s ≥ 1 , error e r r o r 的值为 0 0 。
可以看出来是 err0/1 e r r 0 / 1 的上限。如果我们有一个 err0/1 e r r 0 / 1 的上限,我们可以使用这个上限来推导一些算法来间接的把 err0/1 e r r 0 / 1 做好。 所以可以把 soft margin SVM s o f t m a r g i n S V M 看做是在间接的把 err0/1 e r r 0 / 1 做好。 errsvm e r r s v m 被称为是 hinge error measure h i n g e e r r o r m e a s u r e (合页损失)。
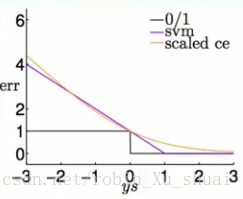
将 logistics error l o g i s t i c s e r r o r 也画在图中可以得到:
- errsce(s,y)=log2(1+exp(−ys)) e r r s c e ( s , y ) = l o g 2 ( 1 + e x p ( − y s ) )
可以从图中看出来, logistic error l o g i s t i c e r r o r 和 hinge error h i n g e e r r o r 有点相似。
−∞ − ∞ ⟵ ⟵ ys y s ⟶ ⟶ +∞ + ∞ ≈−ys ≈ − y s errsvm(s,y) e r r s v m ( s , y ) = 0 ≈−ys ≈ − y s (ln2)errsce(s,y) ( l n 2 ) e r r s c e ( s , y ) = 0 通过上面的分析得到 logistic error l o g i s t i c e r r o r 和 hinge error h i n g e e r r o r 非常的相似,那么 soft margin SVM s o f t m a r g i n S V M 就有点像是在做带有 L2 regularized L 2 r e g u l a r i z e d 的 logistic regression l o g i s t i c r e g r e s s i o n 。即:
L2 regularized logistic regression≈soft margin SVM L 2 r e g u l a r i z e d l o g i s t i c r e g r e s s i o n ≈ s o f t m a r g i n S V M
因为一方面在最佳化的目标函数中存在由于 SVM S V M 自身要求的 large margin l a r g e m a r g i n 而对 w w 的长度做限制的项(),另一方面 SVM S V M 使用的 hinge error h i n g e e r r o r 和逻辑斯蒂回归使用的 err e r r 又非常的接近。
2.2 - Linear Model for Binary Classification
现在我们有了更多的可以用来做 binary classification b i n a r y c l a s s i f i c a t i o n 的 linear model l i n e a r m o d e l 。
-
PLA
P
L
A
算法
PLA P L A 算法直接最小化 err0/1 e r r 0 / 1 , 但是只能用于线性可分的情形,如果不是线性可分的数据,需要使用 Pocket P o c k e t 算法。 -
Regularized Logistic Regression for Classification
R
e
g
u
l
a
r
i
z
e
d
L
o
g
i
s
t
i
c
R
e
g
r
e
s
s
i
o
n
f
o
r
C
l
a
s
s
i
f
i
c
a
t
i
o
n
算法
正则化的逻辑斯蒂回归:使用 GD G D 算法/ SGD S G D 算法最小化加了规则化因子的 errsce e r r s c e
- 优点是容易做最优化,并且可以通过加 regularizer r e g u l a r i z e r 来控制模型的复杂度;
- 缺点是只是在优化 err0/1 e r r 0 / 1 的一个上限;
-
soft margin SVM
s
o
f
t
m
a
r
g
i
n
S
V
M
算法
使用 quadratic programming q u a d r a t i c p r o g r a m m i n g 算法来最小化加了规则化因子的 errsvm e r r s v m
- 优点是容易做最优化,因为 SVM S V M 是从 large margin l a r g e m a r g i n 出发的,所以在模型的复杂度上有一定的保证;
- 缺点是同样也是在最佳化 err0/1 e r r 0 / 1 的上限;
所以我们可以认为 regularized logistic regression r e g u l a r i z e d l o g i s t i c r e g r e s s i o n 几乎就是在做 soft margin SVM s o f t m a r g i n S V M 。如果已经解决了一个 regularized logistic regression r e g u l a r i z e d l o g i s t i c r e g r e s s i o n , 就几乎是求解了一个 soft margin SVM s o f t m a r g i n S V M 的问题。
我们想要问的是:如果我们解决了一个 soft margin SVM s o f t m a r g i n S V M 的问题, 我们是否可以将这个解用在 logistic regression l o g i s t i c r e g r e s s i o n 里面呢? logistic regression l o g i s t i c r e g r e s s i o n 想要给出的一个属于 (0,1) ( 0 , 1 ) 值之间的概率值。小结:如果求解了一个 regularized logistic regression r e g u l a r i z e d l o g i s t i c r e g r e s s i o n 问题,我们可以说我们几乎得到了一个 SVM S V M 的解;那如果我们解决了一个 SVM S V M 是不是也可以说得到了 regularized logistic regression r e g u l a r i z e d l o g i s t i c r e g r e s s i o n 的解,也能够给出一个样本属于正例的概率呢?
3 - SVM for Soft Binary Classification
如何将 SVM S V M 用在 soft binary classification s o f t b i n a r y c l a s s i f i c a t i o n 上呢?也就是说,不再仅仅是想让 SVM S V M 只是输出一个类别,而是输出属于某一个类别的概率。
思路1:既然 SVM S V M 和 logistics regression l o g i s t i c s r e g r e s s i o n 这么像,不如我们就将 soft margin SVM s o f t m a r g i n S V M 的解 (wsvm,bsvm) ( w s v m , b s v m ) 当做是 logistics regression l o g i s t i c s r e g r e s s i o n 的近似解。
- 使用 SVM S V M 算法得到 (wsvm,bsvm) ( w s v m , b s v m ) ;
- 将 SVM S V M 的解当成是 logistics regression l o g i s t i c s r e g r e s s i o n 的近似解。返回 soft classifier s o f t c l a s s i f i e r 分类器 g(x)=θ(wTsvmx+bsvm) g ( x ) = θ ( w s v m T x + b s v m ) ;
直接使用了 SVM S V M 和 logistics regression l o g i s t i c s r e g r e s s i o n 的相似性,这样的方法通常表现的还不错,但是在这个方法中几乎没有了 logistics regression l o g i s t i c s r e g r e s s i o n 的特点,例如 maximum likelihood m a x i m u m l i k e l i h o o d ;
思路2:如果我们想要保留 logistics regression l o g i s t i c s r e g r e s s i o n 的特点的话,比如保留极大似然概率这样的学习的规则。 我们可能的一个做法是:将 SVM S V M 的结果作为 logistics regression l o g i s t i c s r e g r e s s i o n 的 GD G D 算法或者是 SGD S G D 算法的初始值。这样可能会比较快的得到 logistics regression l o g i s t i c s r e g r e s s i o n 的结果。
- 使用 SVM S V M 算法得到 (wsvm,bsvm) ( w s v m , b s v m ) ;
- 将 (wsvm,bsvm) ( w s v m , b s v m ) 作为 gradient descent g r a d i e n t d e s c e n t 或者是 stochastic gradient descent s t o c h a s t i c g r a d i e n t d e s c e n t 的初始值 w0 w 0 ;
- 返回分类器: g(x)=θ(wTx+b) g ( x ) = θ ( w T x + b ) ;
问题是这样做的结果和直接使用 logistics regression l o g i s t i c s r e g r e s s i o n 得到的结果几乎是没有什么差别的。这样的方法又缺失了 SVM S V M 算法的特点,比如 non linear n o n l i n e a r 的 kernel SVM k e r n e l S V M 技巧在这个方法中其实起不到很大的作用。
3.1 - Platt’s Model
为了融合 SVM S V M 和 logistic regression l o g i s t i c r e g r e s s i o n 各自的特点。我们提出了如下的模型:
Two Level Learning
g(x)=θ(A⋅(wTsvmΦ(x)+bsvm)+B) g ( x ) = θ ( A ⋅ ( w s v m T Φ ( x ) + b s v m ) + B )对通过 SVM S V M 算法得到的分数 wTsvmΦ(x)+bsvm w s v m T Φ ( x ) + b s v m ,使用两个参数 A A 和分别进行放缩和平移,使用 logistic regression l o g i s t i c r e g r e s s i o n 对这两个参数进行训练,以满足 maximum likelihood m a x i m u m l i k e l i h o o d 的需求。
因为内层使用的是 SVM S V M ,所以任何 SVM S V M 中的 dual d u a l , kernel k e r n e l 都是可以使用的。- SVM flavor:找出超平面的法向量 wsvm w s v m
- LogReg flavor:fine-tune hyperplane to match maximum likelihood by scaling( A A ) and shifting()。即通过缩放和平移微调超平面,使得似然函数极大。
通常 A>0 A > 0 并且 B≈0 B ≈ 0 ,如果 SVM S V M 的效果好的话。
LogReg on SVM-transformed data
minA,B1N∑n=1Nlog(1+exp(−yn(A⋅(wTsvmΦ(x)+bsvmΦsvm(xn))+B))) m i n A , B 1 N ∑ n = 1 N l o g ( 1 + e x p ( − y n ( A ⋅ ( w s v m T Φ ( x ) + b s v m ⏟ Φ s v m ( x n ) ) + B ) ) )通过分析可以认为 wTsvmΦ(x)+bsvm w s v m T Φ ( x ) + b s v m 是通过 SVM S V M 算法给出的一个特别的特征转换,我们称之为 Φsvm(xn) Φ s v m ( x n ) ,这个特别的转换将输入空间的特征从多维转换到了一维。那么在下一步使用 logistic regression l o g i s t i c r e g r e s s i o n 的时候,其实我们面对的是一个一维空间中的最优化问题,这个最优化的问题有两个需要优化的变量只有两个 A,B A , B 。所以总结该方法分为两个阶段:第一个阶段做 SVM S V M ,将 SVM S V M 当做是一个转换。第二个阶段做一个简单的 logReg l o g R e g 问题。(融合 SVM S V M 的逻辑斯蒂回归模型)
Probabilistic SVM P r o b a b i l i s t i c S V M
Platt′s Model Probabilistic SVM for Soft Binary Classification P l a t t ′ s M o d e l P r o b a b i l i s t i c S V M f o r S o f t B i n a r y C l a s s i f i c a t i o n- 在数据 D D 上运行得到 (bsvm,wsvm) ( b s v m , w s v m ) (或者是等价的 α α ),此时也就得到了一个转化 z′=wTsvmΦ(x)+bsvm z ′ = w s v m T Φ ( x ) + b s v m 。并且这个转换是从多维到一维的。
- 在新的数据集 {(z′n,yn)} { ( z n ′ , y n ) } 上运行 LogReg L o g R e g 得到 A,B A , B
- 得到分类器: g(x)=θ(A⋅(wTsvmΦ(x)+bsvm)+B) g ( x ) = θ ( A ⋅ ( w s v m T Φ ( x ) + b s v m ) + B )
使用对偶的带有 kernel k e r n e l 的方式求解得到的模型的最终的长相:
θ(A∑SV ynαnK(xn,x)+Ab+B) θ ( A ∑ S V y n α n K ( x n , x ) + A b + B )现在我们就从 SVM S V M ,特别是 Kernel SVM K e r n e l S V M 得到了 Logistic Regression L o g i s t i c R e g r e s s i o n 在 Z Z 空间中的。
3.2 - 小结
我们通过带有 kernel k e r n e l 的 SVM S V M 得到了 logistic regression l o g i s t i c r e g r e s s i o n 在 Z Z 空间中的,但是并没有真的在 Z Z 空间中求解,而是利用了 SVM S V M 和 logistic regression l o g i s t i c r e g r e s s i o n 的相似性,使用 kernel SVM k e r n e l S V M 在 Z Z 空间中求解,然后再使用和 B B 来微调,这样来得到在空间中可能的 logistic regression l o g i s t i c r e g r e s s i o n 还不错的解。但是这还不是在 Z Z 空间中最好的解。 如果想要在 Z Z 空间中找到的最好的解,该怎么做呢?下一节会给出答案。
4 - Kernel Logistic Regression
上一小节上中我们提到说想要在 Z Z 空间中做,而不只是想要上一小节中得到的近似解。
首先想一下 SVM S V M 是怎么能够在 Z Z 空间中寻找超平面的,首先是一个二次规划问题,可以将原问题转换为对偶问题,并且发现对偶问题只需要计算 Z Z 空间中的內积,这时就可以引入来进行计算。从而能在 Z Z 空间中找到一个分隔超平面。
简单的来说,就是将 Z Z 空间的內积运算换成可以在空间中轻易计算的內积的函数。在原来的 SVM S V M 中主要有两个地方会用到 kernel trick k e r n e l t r i c k :第一个是在训练的过程中需要 Z Z 空间中的內积运算;第二个是在预测的过程中,即需要和 z z 的內积。只有在可以表示为所有的 z z (这些是原始在 X X 空间中的数据通过特征转换得到的)的线性组合的情况下,这样才能把在预测过程中计算和 z z (新的样本)的內积的过程表示成的形式。例如在 SVM S V M 中,在预测过程中需要计算 w w 和的內积,而 w=∑βnzn w = ∑ β n z n ,所以 wTz=∑βnzTnz=∑βnK(xn,x) w T z = ∑ β n z n T z = ∑ β n K ( x n , x ) 。最佳的 w w 是的线性组合是我们能够使用 kernel k e r n e l 的关键。也就是说如果最佳的 w w 可以被表达出来,那么我们就可以使用 kernel k e r n e l 。那么问题来了,什么时候 w w 可以被表达出来呢?
4.1 - Represent Theorem
对于任何 L2 L 2 - regularized r e g u l a r i z e d 的线性模型,也就是说目标函数中存在 w w 的平方:
那么最好的 w w 可以表示为的线性组合:
w∗=∑n=1Nβnzn w ∗ = ∑ n = 1 N β n z n证明:假设我们有最佳的解 w∗ w ∗ ,这个向量可以分成两个部分 w∗=w||+w⊥ w ∗ = w | | + w ⊥ , 其中 w|| w | | 表示可以使用 zn z n 表示出来的; w⊥ w ⊥ 表示不可以被 zn z n 标示出来的。即 w||∈span(zn),w⊥⊥span(zn) w | | ∈ s p a n ( z n ) , w ⊥ ⊥ s p a n ( z n ) 。所以如果 w∗ w ∗ 可以被 z z 表示出来的话,应该有的是。
我们考虑如果 w⊥≠0 w ⊥ ≠ 0 会发生什么呢?
- 首先我们可以得到的是: err(yn,wT∗zn)=err(yn,(w||+w⊥)Tzn)=err(yn,w||)Tzn e r r ( y n , w ∗ T z n ) = e r r ( y n , ( w | | + w ⊥ ) T z n ) = e r r ( y n , w | | ) T z n
- 其次考虑另一个部分, wT∗w∗=(w||+w⊥)T(w||+w⊥)=wT||w||+2wT||w⊥+wT⊥w⊥=wT||w||+wT⊥w⊥>wT||w|| w ∗ T w ∗ = ( w | | + w ⊥ ) T ( w | | + w ⊥ ) = w | | T w | | + 2 w | | T w ⊥ + w ⊥ T w ⊥ = w | | T w | | + w ⊥ T w ⊥ > w | | T w | | 。因为我们假设 w⊥≠0 w ⊥ ≠ 0 ,所以上面的大于号是成立的。
之前说 w∗ w ∗ 是最佳解,但是现在发现,如果 w⊥≠0 w ⊥ ≠ 0 ,那么 w|| w | | 将是更好的解,这和前提 w∗ w ∗ 是最佳解矛盾,所以 w⊥ w ⊥ 必须等于 0 0 。(为什么是比 w∗ w ∗ 更好的解呢?因为对于目标函数中的想要最小化的两项来说, w|| w | | 和 w∗ w ∗ 在第二项的值相同,第一项的值 w∗ w ∗ 小于 w∗ w ∗ )
所以我们能够得出结论,只要是在解决 L2 L 2 - regularized r e g u l a r i z e d 的线性问题,问题的最优解 w w 就可以被表示,这样我们就可以使用 kernel k e r n e l 函数。 任何的 L2 L 2 - regularized r e g u l a r i z e d 的方法都可以被 kernelized k e r n e l i z e d 。
所以现在我们就利用这个很厉害的结果将 kernel k e r n e l 用在 L2 L 2 - regularized logistic regression r e g u l a r i z e d l o g i s t i c r e g r e s s i o n 上面。
L2 L 2 - regularized logistic regression r e g u l a r i z e d l o g i s t i c r e g r e s s i o n 问题如下:
minwλNwTw+1N∑n=1Nlog(1+exp(−ynwTxn)) m i n w λ N w T w + 1 N ∑ n = 1 N l o g ( 1 + e x p ( − y n w T x n ) )根据上面证明的 Represent Theorem R e p r e s e n t T h e o r e m ,我们已经知道,这个问题最佳的解的长相是 w∗=∑Nn=1βnzn w ∗ = ∑ n = 1 N β n z n 。所以我们可把这个最佳的解带进去,不去求 w w ,而是去求,得到如下的问题:
minβλN∑n=1N∑m=1NβnβmzTnzm+1N∑n=1Nlog(1+exp(−yn∑n=1NβmzTmzn)) m i n β λ N ∑ n = 1 N ∑ m = 1 N β n β m z n T z m + 1 N ∑ n = 1 N l o g ( 1 + e x p ( − y n ∑ n = 1 N β m z m T z n ) )
使用核函数取代里面出现的 Z Z 空间中的內积可以得到:Kernel Logistic Regression
现在问题变为求解 β β 而不是 w w 。变量的个数为, 跟 Z Z 空间的长度没有关系。因为这是一个无条件的最优化问题,所以可以使用算法来进行求解。
4.2 - 从另一个角度来理解KLR
KLR: kernel logistic regression
Kernel Logistic Regression
minβλN∑n=1N∑m=1NβnβmK(xm,xn)+1N∑n=1Nlog(1+exp(−yn∑n=1NβmK(xm,xn))) m i n β λ N ∑ n = 1 N ∑ m = 1 N β n β m K ( x m , x n ) + 1 N ∑ n = 1 N l o g ( 1 + e x p ( − y n ∑ n = 1 N β m K ( x m , x n ) ) )- ∑Nn=1βmK(xm,xn) ∑ n = 1 N β m K ( x m , x n ) :可以看成是 K K 和內积的结果。可以把核函数 K K 想象成一个转换,求和其他的所有的点的相似性, β β 以一定的权重组合这些相似性。
- ∑Nn=1∑Nm=1βnβmK(xm,xn) ∑ n = 1 N ∑ m = 1 N β n β m K ( x m , x n ) :可以看做是一个特殊的 regularized r e g u l a r i z e d : βTKβ β T K β
所以 KLR K L R 可以看做是 β β 的线性模型,在这里 β β 相当于权重因子,这些权重因子组合了经过 Kernel K e r n e l 的转换,并且使用了一个特别的 kernel regularized k e r n e l r e g u l a r i z e d 。
KLR K L R 和 SVM S V M 最大的不同之处是: KLR K L R 大部分的 βn β n 不是 0 0 。而在中大部分的 αn α n 是 0 0 。
5 - 总结
本篇首先将解释成一个和 regularization r e g u l a r i z a t i o n 有关的模型,说明了 soft margin SVM s o f t m a r g i n S V M 其实就是在做一个 L2 regularization L 2 r e g u l a r i z a t i o n ,并且与其相对应的 error e r r o r 是 hinge error h i n g e e r r o r 。随后证明了 soft margin SVM s o f t m a r g i n S V M 其实几乎就是 L2 regularized logistic regression L 2 r e g u l a r i z e d l o g i s t i c r e g r e s s i o n 。所以如果我们已经解决了一个 SVM S V M 问题,可以通过第二阶段的训练将其变成一个 soft binary classification s o f t b i n a r y c l a s s i f i c a t i o n 的模型。通过 Represent Theorem R e p r e s e n t T h e o r e m 可以解一个在 Z Z <script type="math/tex" id="MathJax-Element-4196">Z</script>空间中的逻辑斯蒂回归问题,但是它的解不是稀疏的。
- soft-margin SVM:





















 3461
3461











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








