因果推断系列13----倾向得分

加载第三方包即相应的全局设定

import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
from causalinference import CausalModel

import graphviz as gr

%matplotlib inline

style.use("fivethirtyeight")
pd.set_option("display.max_columns", 6)
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False

1.问题的提出

积极心理学研究人类行为的积极因素，探究如何过上更好的生活。你可以将它看作是自助书籍与统计学学术严谨性的交汇点。积极心理学最著名的发现之一是成长心态。这个想法是，人们可以拥有固定心态或成长心态。如果你有固定心态，你会认为能力是与出生时或儿童早期固定的。因此，智力是固定的，终身无法改变。如果你到现在为止还没有它，那么你永远不会学会。这个思想的推论是你不应该浪费时间在自己不擅长的领域上，因为你永远学不会如何处理它们。另一种想法是，如果你有成长心态，你会认为智力可以被开发。这个想法的直接结果是你把失败看作是学习过程的一部分，而不是缺乏坚韧的表现。

我们不讨论哪种心态更准确或者说更好，这不是我们的主题。重要的是心理学家发现，拥有成长心态的人倾向于在生活中表现得更好。他们更有可能实现自己设定的目标。

尽管我们已经了解因果推断，但我们已经学会怀疑这些陈述。是成长心态导致人们取得更多的成就呢？还是说那些取得更多成就的人由于成功的结果而倾向于发展成长心态？换句话说，是先有鸡还是先有蛋？在潜在结果符号中，我们有理由相信这些陈述存在偏见。$Y_0|T=1$ 可能大于 $Y_0|T=0$，这意味着即使拥有固定心态的人也会取得更多的成就。

为了解决这个问题，研究人员设计了 The National Study of Learning Mindsets，这是一项在美国公立高中进行的随机研究，旨在找到成长心态的影响。它的研究方式是，学生从学校接受一个研讨会，以了解成长心态。然后，他们在大学学习期间跟踪学生，以衡量他们的学术表现。这种测量被编制成一个成就分数并标准化。为了保护学生的隐私，这项研究的真实数据不公开提供。但是，我们有一个由 Athey and Wager提供的具有相同统计属性的模拟数据集，接下来我们将使用这个数据。

除了被处理变量和结果变量，该研究还记录了一些其他特征：

• schoolid：学生学校的标识符；
• success_expect：未来成功的自我报告期望值，是先前分配随机化之前测量的先前成就的代理；
• ethnicity：学生种族/族裔的分类变量；
• gender：学生性别的分类变量；
• frst_in_family：学生第一代身份的分类变量，即家庭中第一个上大学的人；
• school_urbanicity：学校级别的城市化分类变量，即农村、郊区等；
• school_mindset：学生的固定心态的学校水平均值，在随机分配之前报告，经过标准化；
• school_achievement：学校成绩水平，由前四届学生的考试成绩和大学准备水平测量得到，经过标准化；
• school_ethnic_minority：学校种族/族裔少数人数，即学生中黑人、拉丁裔或美国土著人的百分比，经过标准化；
• school_poverty：学校贫困集中程度，即家庭收入低于联邦贫困线的学生百分比，经过标准化；
• school_size：学校四个年级总学生人数，经过标准化。

learning_mindset.csv数据下载

data = pd.read_csv("./data/learning_mindset.csv")
data.sample(5, random_state=5)

	schoolid	intervention	achievement_score	...	school_ethnic_minority	school_poverty	school_size
259	73	1	1.480828	...	-0.515202	-0.169849	0.173954
3435	76	0	-0.987277	...	-1.310927	0.224077	-0.426757
9963	4	0	-0.152340	...	0.875012	-0.724801	0.761781
4488	67	0	0.358336	...	0.315755	0.054586	1.862187
2637	16	1	1.360920	...	-0.033161	-0.982274	1.591641

5 rows × 13 columns

虽然该研究是随机的，但该数据并不是无混杂的。如果查看附加特征，会发现它们在处理组和对照组之间有系统性的差异。一个可能的原因是，处理变量是由学生是否参加研讨会来度量的。因此，虽然参加机会是随机的，但参与本身不是随机的。我们在这里处理的是不服从性的情况，其中一个原因是学生的成功期望与参加研讨会有关。成功期望更高的学生更有可能参加成长心态研讨会。

data.groupby("success_expect")["intervention"].mean()

success_expect
1    0.271739
2    0.265957
3    0.294118
4    0.271617
5    0.311070
6    0.354287
7    0.362319
Name: intervention, dtype: float64

不过，让我们看看平均值差异$E[Y|T=1]-E[Y|T=0]$看起来是什么。这将是一个进行比较的有用基准。

smf.ols("achievement_score ~ intervention", data=data).fit().summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	-0.1538	0.012	-13.201	0.000	-0.177	-0.131
intervention	0.4723	0.020	23.133	0.000	0.432	0.512

简单地比较有和没有干预的人，我们可以看到，处理组的成绩平均比未处理组高0.3185（0.4723-0.1538）。但这是大还是小呢？我知道对标准化结果进行解释可能会存在难度，我们要学会如何解释标准化分数。

结果变量被标准化意味着它是以标准差度量的。因此，处理组比未处理组高0.3185个标准差。这就是它的意思。至于这是大还是小，让我们记住一些关于正态分布的知识。我们知道它在2个标准差之间的置信区间是95%，左右尾部各剩下2.5%。这也意味着如果某人的得分比平均值高2个标准差，则所有个体中97.5％（95％加上左侧2.5％尾部）的个体都低于该人。通过查看正态分布的CDF，我们知道在1个标准差以下它的置信区间约85％，在0.5个标准差以下它的置信区间约70％。由于处理组的平均标准化得分约为0.5，这意味着他们在个人成就方面的排名约为前30％。换句话说，他们是成就更高的前30％的个体。如下图所示：

plt.hist(data["achievement_score"], bins=20, alpha=0.3, label="All")
plt.hist(data.query("intervention==0")["achievement_score"], bins=20, alpha=0.3, color="C2")
plt.hist(data.query("intervention==1")["achievement_score"], bins=20, alpha=0.3, color="C3")
plt.vlines(-0.1538, 0, 300, label="Untreated", color="C2")
plt.vlines(-0.1538+0.4723, 0, 300, label="Treated", color="C3")
plt.legend();

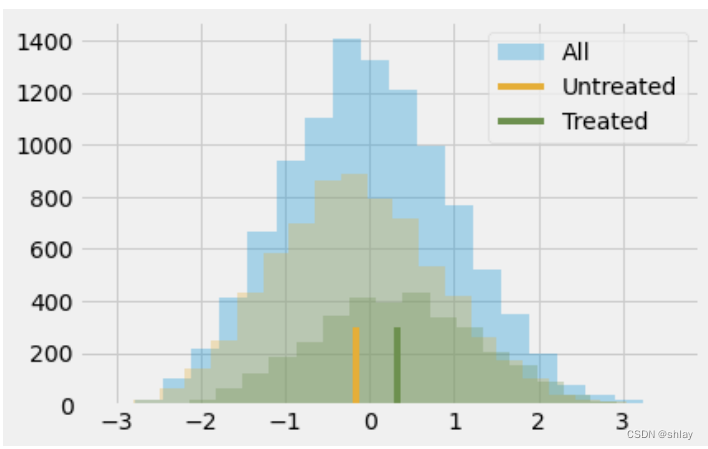
当然，我们仍然认为这个结果存在偏差。处理组和对照组之间的差异可能比这个小，因为我们认为偏差是正的。我们已经看到更有抱负的人更愿意去参加研讨会，所以即使他们没有参加研讨会，他们可能也会取得更好的成果。为了控制这种偏差，我们可以使用回归或匹配，现在我们来学习一种新的技术：倾向得分。

2. 倾向得分

倾向得分源于这样一个认识：您不需要直接控制混杂因素 X 来实现条件独立 $(Y_1,Y_0)\perp T|X$。相反，仅需要控制一个平衡分数 $E[T|X]$ 即可。这个平衡分数通常是个体接受处理的条件概率，即 $P(T|X)$，也称为倾向得分 $P(x)$。倾向得分使得您不必在 X 的全部条件下实现潜在结果对处理的独立性，而只需在这个单一变量即倾向得分的条件下实现即可：

$(Y_1,Y_0)\perp T|P(x)$

这一原理有严谨的数学证明，但我们也可以用更直观的方式来处理这个问题。倾向得分是接受处理的条件概率，对吧？因此，我们可以将其视为一种将 X 转换为处理 T 的函数。倾向得分将变量 X 和处理 T 之间的这个中间区域联系在一起。如在因果图中展示这个关系，如下图所示：

g = gr.Digraph()
g.edge("T", "Y")
g.edge("X", "Y")
g.edge("X", "P(x)")
g.edge("P(x)", "T")
g

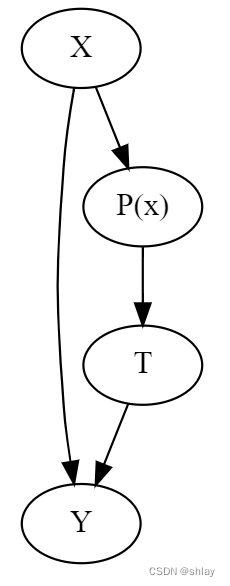
如果我知道 $P(x)$ 是什么，就会了解$X$ 能帮助我们了解 $T$ 可能的值。这意味着控制 $P(x)$ 的效果与直接控制 $X$ 的效果相同。从我们的心态计划来看。受处理和未受处理者最初是不可比较的，因为更有抱负的人既更可能接受处理，也更有可能在生活中取得更多成就。但是，如果我从处理组和对照组中各取一名个体，但两者接受处理的概率相同，则它们是可比的。想想看，如果他们接受处理的概率完全相同，那么其中一个接受处理而另一个没有接受处理的唯一原因纯粹是因为偶然。保持倾向分数不变的作用类似于使数据看起来像随机数据。

现在，我们有了直观的了解，让我们看一下数学证明。我们要证明 $(Y_1,Y_0)\perp T|P(x)$ 等价于 $E[T|P(x),X]=E[T|P(x)]$

也就是说，一旦对 $P(x)$ 进行了条件控制，$X$ 就不能给我们关于 $T$ 的额外信息。证明方法非常奇怪。我们将通过将上述等式转换来证明它。首先看一下左侧的 $E[T|P(x),X]$。

$E[T|P(x),X]=E[T|X]=P(x)$

我们知道 $P(x)$ 只是 $X$ 的一个函数，因此在我们已经对 $X$ 进行了条件控制后，对它进行条件控制不会提供进一步的信息。然后，我们使用倾向分数的定义 $E[T|X]$。

对于右边，我们将使用重复期望法则 $E[A]=E[E[A|B]]$。该法则表明，我们可以通过查看按 $B$ 分解的 $A$ 值，然后平均它来计算 $A$ 的期望值。

$E[T|P(x)]=E[E[T|P(x),X]|P(x)]=E[P(x)|P(x)]=P(x)$

第一个等式来自重复期望法则。第二个等式来自我们处理左侧时发现的东西。由于左右两侧都相等，即 $P(x)$，显然这个等式是成立的。

3.加权倾向得分

好了，我们已经得到了倾向得分，现在该怎么做？就像我说的，我们只需要对其进行条件化。例如，我们可以运行一个仅在倾向性分数上进行条件化的线性回归，而不是在所有的X上进行条件化。现在，让我们来看一种只使用倾向性分数而不使用其他方法。这个想法是用倾向性分数来写出条件平均数的差异

$E[Y|X,T=1]-E[Y|X,T=0]=E[\frac{Y}{P(x)}|X,T=1]P(x)-E[\frac{Y}{(1-P(x))}|X,T=0](1-P(x))$

我们可以进一步简化这个式子，但是让我们先这样看一下，它给了我们一些理解倾向得分在做什么的很好视角。第一个项是估计$Y_1$。它取所有接受处理的人，然后用接受处理的概率的倒数进行缩放。这样做的原因是使那些处理概率非常低的人具有高的权重。这是有道理的，对吧？如果一个人接受处理的概率很低，那个人看起来就像未接受处理的人。然而，同一个人确实接受了处理。我们有一个看起来像未接受处理但实际接受处理的人，因此我们会给这个个体一个很高的权重。这样就创建了一个与原始数据集大小相同的人群，但其中每个人都接受了处理。同理，另一项是查看未接受处理的人，并给那些看起来像接受处理的人以高的权重。由于该估计器将每个单位按接收某种处理的概率进行缩放，因此称为处理概率的倒数加权（IPTW）。

下图是这个权重法的效果。

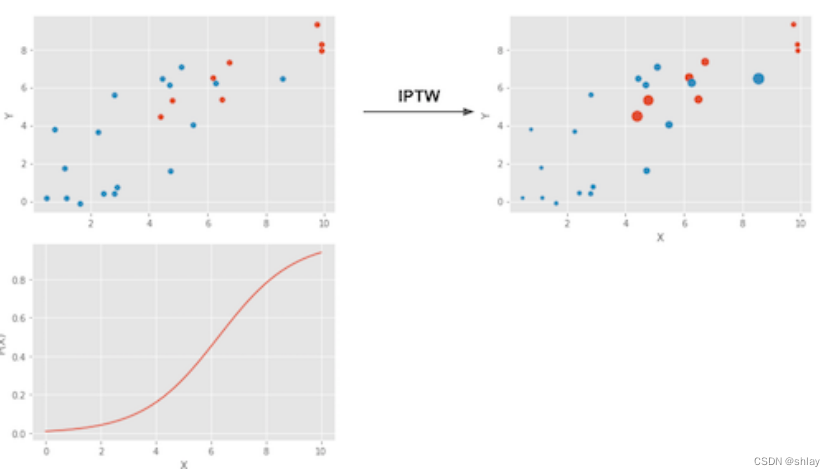
左上图显示了原始数据。蓝色点是未接受处理的，红色点是接受处理的。底部图显示了倾向性分数$P(x)$。请注意，它在0和1之间，随着X的增加而增加。最后，右上图是加权数据。请注意，向左移动（倾向得分较低）的红色。

现在我们可以简化上面的表达式为：

$E\left[Y\frac{T-P(x)}{P(x)(1-P(x))}\right|X]$

如果我们对X进行积分，那么它就变成了我们的倾向得分加权估计器。

$E\left[Y\frac{T-P(x)}{P(x)(1-P(x))}\right]$

请注意，此估计器要求$P(x)$和$1-P(x)$都大于零。简而言之，这意味着每个人都至少有一定概率接受处理和不接受处理。另一种表述方式是，接受处理和未接受处理的分布需要重叠。这是因果推断的正性假设。也很好理解，如果接受处理和未接受处理的个体不重叠，那就意味着它们非常不同，我们将无法推断一组对另一组的影响。这种推断不是不可能的（回归可以做到），但是非常危险。这就像在只有男性接受处理的实验中测试新药物，然后假设它对女性的效应与男性一样。

4. 估计倾向得分

在理想情况下，我们会有真正的倾向得分 $P(x)$。然而，在现实中，分配处理的机制是未知的，我们需要用估计值 $\hat{P}(x)$ 来替换真实的倾向得分。常用的一种方法是使用逻辑回归，但也可以使用其他机器学习方法，如Gradient Boosting，尽管这需要一些额外的步骤来避免过拟合。

在这里，我将坚持使用逻辑回归。这意味着我们需要将数据集中的分类变量转换为虚拟变量。

categ = ["ethnicity", "gender", "school_urbanicity"]
cont = ["school_mindset", "school_achievement", "school_ethnic_minority", "school_poverty", "school_size"]

data_with_categ = pd.concat([
    data.drop(columns=categ), # dataset without the categorical features
    pd.get_dummies(data[categ], columns=categ, drop_first=False)# categorical features converted to dummies
], axis=1)

print(data_with_categ.shape)

(10391, 32)

现在我们用logistic回归来估计倾向得分。

from sklearn.linear_model import LogisticRegression

T = 'intervention'
Y = 'achievement_score'
X = data_with_categ.columns.drop(['schoolid', T, Y])

ps_model = LogisticRegression(C=1e6).fit(data_with_categ[X], data_with_categ[T])

data_ps = data.assign(propensity_score=ps_model.predict_proba(data_with_categ[X])[:, 1])

data_ps[["intervention", "achievement_score", "propensity_score"]].head()

	intervention	achievement_score	propensity_score
0	1	0.277359	0.315503
1	1	-0.449646	0.263804
2	1	0.769703	0.344043
3	1	-0.121763	0.344043
4	1	1.526147	0.367799

首先，我们可以确保倾向得分权重确实重新构建了一个每个个体都接受处理的总体。通过生成权重 $1/P(x)$，它创建了一个每个人都接受处理的总体，并提供权重 $1/(1-P(x))$，创建了每个人都未接受处理的总体。

weight_t = 1/data_ps.query("intervention==1")["propensity_score"]
weight_nt = 1/(1-data_ps.query("intervention==0")["propensity_score"])
print("Original Sample Size", data.shape[0])
print("Treated Population Sample Size", sum(weight_t))
print("Untreated Population Sample Size", sum(weight_nt))

Original Sample Size 10391
Treated Population Sample Size 10388.402873229075
Untreated Population Sample Size 10391.501375657612

我们还可以使用倾向得分来发现混杂变量。如果总体的一个分组比另一个分组具有更高的倾向得分，则意味着某些非随机因素影响了处理。如果这个因素也影响结果变量，那么我们就有了混杂变量。在我们的例子中，我们可以看到更有雄心壮志的学生也更有可能参加成长心态研讨会。

sns.boxplot(x="success_expect", y="propensity_score", data=data_ps)
plt.title("存在混杂")

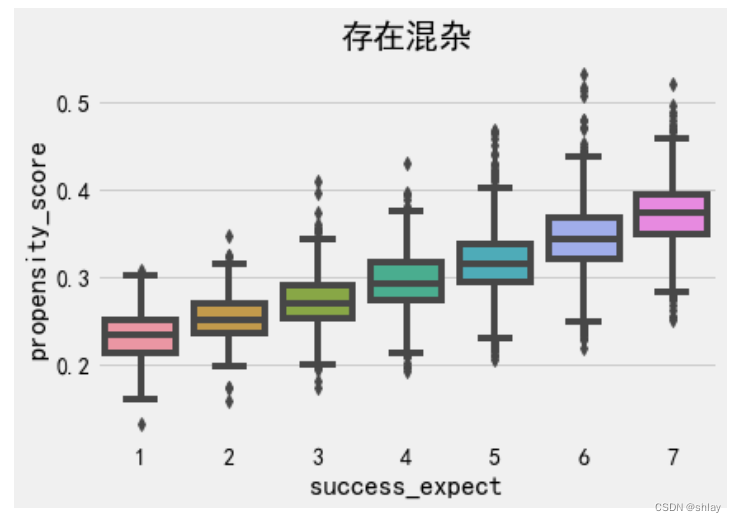
我们还必须检查接受处理和未接受处理的总体之间是否存在重叠。为此，我们可以查看未接受处理和接受处理总体倾向得分的经验分布。从下面的图片可以看出，没有人的倾向得分为零，即使在倾向得分较低的区域，我们也可以找到接受处理和未接受处理的个体。这就是我们所说的总体中接受处理和未接受处理的群体得分均衡。

sns.distplot(data_ps.query("intervention==0")["propensity_score"], kde=False, label="Non Treated")
sns.distplot(data_ps.query("intervention==1")["propensity_score"], kde=False, label="Treated")
plt.title("正性检验")
plt.legend()

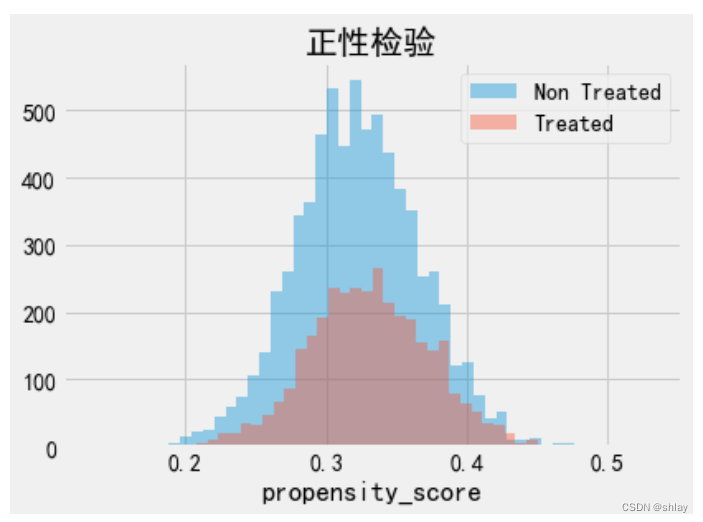
最后，我们可以使用倾向得分加权估计器来估计平均处理效应。

weight = ((data_ps["intervention"]-data_ps["propensity_score"]) /
          (data_ps["propensity_score"]*(1-data_ps["propensity_score"])))

y1 = sum(data_ps.query("intervention==1")["achievement_score"]*weight_t) / len(data)
y0 = sum(data_ps.query("intervention==0")["achievement_score"]*weight_nt) / len(data)

ate = np.mean(weight * data_ps["achievement_score"])

print("Y1:", y1)
print("Y0:", y0)
print("ATE", np.mean(weight * data_ps["achievement_score"]))

Y1: 0.25959115218939305
Y0: -0.12893047035866634
ATE 0.3885216225480566

倾向得分加权估计说，我们应该预期接受处理的个体在成就方面比未接受处理的同龄人高出0.38个标准差。我们还可以看到，如果没有人接受处理，我们应该预期成就的总体水平比现在低0.12个标准差。按照相同的推理，如果我们给每个人都提供了研讨会，我们应该预期成就的总体水平比现在高0.25个标准差。相比之下，我们仅通过比较接受处理和未接受处理得到了0.47的平均处理效应估计值。这表明我们的偏差确实是正的，控制X给我们提供了更合理的成长心态影响估计。

5. 标准误差

要计算IPTW估计器的标准误差，我们可以使用加权平均值的方差公式。

${\sigma }_w^2=\frac{{\sum }_{i=1}^n{w}_i(y_i-\hat{\mu }{)}^2}{{\sum }_{i=1}^n{w}_i}$

然而，只有在我们拥有真实的倾向得分$P(x)$时，我们才能使用这个公式。如果我们使用估计得到的倾向得分$\hat{P}(x)$，我们需要考虑这个估计过程中的误差。最简单的做法是通过自助法对整个过程进行抽样，从原始数据中进行有放回地抽样，像我们上面所做的那样计算ATE。我们重复这个过程很多次，得到ATE估计的分布。

from joblib import Parallel, delayed # for parallel processing

# define function that computes the IPTW estimator
def run_ps(df, X, T, y):
    # estimate the propensity score
    ps = LogisticRegression(C=1e6).fit(df[X], df[T]).predict_proba(df[X])[:, 1]
    
    weight = (df[T]-ps) / (ps*(1-ps)) # define the weights
    return np.mean(weight * df[y]) # compute the ATE

np.random.seed(88)
# run 1000 bootstrap samples
bootstrap_sample = 1000
ates = Parallel(n_jobs=4)(delayed(run_ps)(data_with_categ.sample(frac=1, replace=True), X, T, Y)
                          for _ in range(bootstrap_sample))
ates = np.array(ates)

ATE是bootstrap样本的平均值。为了获得置信区间，我们可以检查bootstrap分布的分位数。对于95%置信区间，我们使用2.5和97.5百分位数。

print(f"ATE: {ates.mean()}")
print(f"95% C.I.: {(np.percentile(ates, 2.5), np.percentile(ates, 97.5))}")

ATE: 0.3877468027463349
95% C.I.: (0.35447047390804165, 0.41992765162057555)

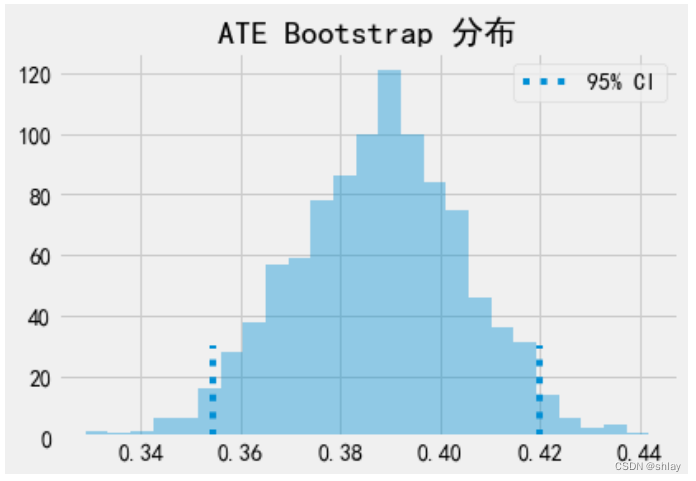
我们还可以可视化bootstrap样本和置信区间。

sns.distplot(ates, kde=False)
plt.vlines(np.percentile(ates, 2.5), 0, 30, linestyles="dotted")
plt.vlines(np.percentile(ates, 97.5), 0, 30, linestyles="dotted", label="95% CI")
plt.title("ATE Bootstrap 分布")
plt.legend();

6. 倾向得分模型的常见问题

作为一名数据科学家，我知道使用机器学习工具包的全部功能来尽可能精确地估计倾向得分可能是很诱人的。你可能很容易陷入所有AUC优化、交叉验证和贝叶斯超参数调整的泥潭中。现在，我不是说你不应该这样做。实际上，关于倾向得分和机器学习的所有理论都是非常新的，所以还有很多我们不知道的东西。
首先，倾向得分的预测质量并不能转化为它的平衡属性。作为机器学习领域的从业者，熟悉因果推断最具挑战性的一个方面是不要将所有问题都视为预测问题。事实上，最大化倾向得分的预测能力可能会损害因果推断的目标。倾向得分不需要非常好地预测处理。它只需要包括所有混杂变量。实际上，如果我们包含了对处理变量具有很好的预测能力但是对结果变量没有影响的变量，这会增加倾向得分估计器的方差。这类似于线性回归在包括与处理相关但与结果不相关的变量时面临的问题。

为了说明这一点，请考虑以下示例（改编自Hernán的书）。你有两所学校，其中一所99%的学生参加成长心态研讨会，另一所仅1％的学生参加。假设学校对处理效应没有影响，因此无需控制。如果将学校变量添加到倾向得分模型中，它将具有非常高的预测能力。但是，由于偶然性，我们可能会得到一个样本，其中A学校的所有人都接受了处理，导致该学校的倾向得分为1，这将产生无限方差。这是一个极端的例子，我们可以通过模拟数据进行验证。

np.random.seed(42)
school_a = pd.DataFrame(dict(T=np.random.binomial(1, .99, 400), school=0, intercept=1))
school_b = pd.DataFrame(dict(T=np.random.binomial(1, .01, 400), school=1, intercept=1))
ex_data = pd.concat([school_a, school_b]).assign(y = lambda d: np.random.normal(1 + 0.1 * d["T"]))
ex_data.head()

	T	school	intercept	y
0	1	0	1	0.309526
1	1	0	1	1.571468
2	1	0	1	2.982024
3	1	0	1	2.445420
4	1	0	1	2.693187

经过模拟数据后，我们通过bootstrap运行两次倾向得分算法。第一次将学校作为倾向得分模型的特征之一。第二次在模型中不包括学校。

ate_w_f = np.array([run_ps(ex_data.sample(frac=1, replace=True), ["school"], "T", "y") for _ in range(500)])
ate_wo_f = np.array([run_ps(ex_data.sample(frac=1, replace=True), ["intercept"], "T", "y") for _ in range(500)])

sns.distplot(ate_w_f, kde=False, label="PS W School")
sns.distplot(ate_wo_f, kde=False, label="PS W/O School")
plt.legend()

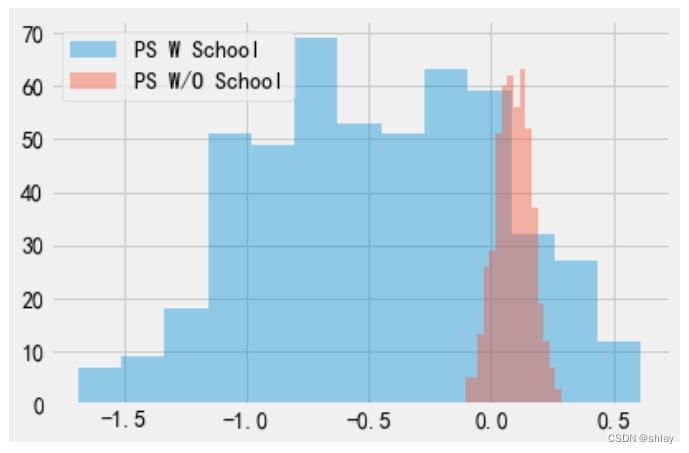
正如您所看到的，添加学校特征的倾向得分估计器具有巨大的方差，而没有它的估计器更加稳定。另外，由于学校不是混杂因素，没有包括学校的模型也没有偏差。就像我所说的，简单地预测处理效应不是这个问题的关键。实际上我们需要以一种控制混杂的方式构建预测，而不是以一种预测处理的方式。

这将导致倾向得分方法中经常遇到的另一个问题。在我们的心态案例中，数据非常平衡。但某些情况下，接受处理的人比未接受处理的人有更高的处理概率，而且倾向得分分布并不重叠。

sns.distplot(np.random.beta(4,1,500), kde=False, label="Non Treated")
sns.distplot(np.random.beta(1,3,500), kde=False, label="Treated")
plt.title("正性假设检验")
plt.legend()

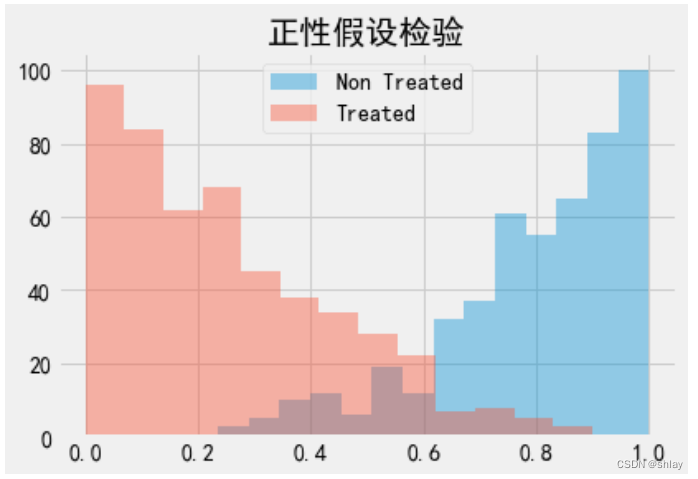
如果出现这种情况，表明正性假设不是很强。例如，如果接受处理的人有0.9的倾向得分，而未接受处理的人的最大倾向得分为0.7，我们将没有可以与具有0.9倾向得分的处理个体进行比较的未接受处理的人。这种不平衡可能会产生一些偏差，因为我们必须将处理效应外推到未知区域。不仅如此，倾向得分非常高或非常低的个体具有非常高的权重，从而增加了方差。作为一个经验法则，如果任何权重大于20，就比较麻烦（因为这会发生在具有0.95倾向得分的未接受处理的个体或0.05倾向得分的接受处理的个体身上）。

另一种选择是将权重进行截断，使其最大值为20。这将减少方差，但实际上会产生更多的偏差。说实话，尽管这是减少方差的常见做法，但我并不太喜欢它。你永远不会知道你剪切时引入的偏差是否太大。而且，如果分布不重叠，你的数据可能根本不足以得出因果结论。为了进一步了解这一点，我们可以看看结合倾向得分和匹配的技术。

7. 倾向得分匹配

如之前所说，当您有倾向得分时，就不需要控制X。控制它就足够了。因此，您可以将倾向得分视为在特征空间中执行一种降维的方法。它将X中的所有特征压缩成一个单一的处理分配维度。因此，我们可以将倾向得分视为其他模型的输入特征。例如，可以使用回归模型进行建模。

smf.ols("achievement_score ~ intervention + propensity_score", data=data_ps).fit().summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	-3.0771	0.065	-47.056	0.000	-3.205	-2.949
intervention	0.3930	0.019	20.974	0.000	0.356	0.430
propensity_score	9.0556	0.200	45.308	0.000	8.664	9.447

如果我们控制了倾向得分，我们现在估计ATE为0.39，这比之前没有控制倾向得分的回归模型的0.47要低。我们还可以使用倾向得分匹配。这一次，我们不再试图找到在所有X特征上相似的匹配项，而是可以找到具有相同倾向得分的匹配项。

这是匹配估计器的重大改进，因为它解决了维度灾难的问题。而且，如果一个特征对于处理分配不重要，那么倾向得分模型将会学习到这一点，并在拟合处理机制时给予其比较低的重要性。另一方面，如果根据特征进行匹配，仍然会尝试找到个体在此不重要特征上相似的匹配项。

cm = CausalModel(
    Y=data_ps["achievement_score"].values, 
    D=data_ps["intervention"].values, 
    X=data_ps[["propensity_score"]].values
)

cm.est_via_matching(matches=1, bias_adj=True)

print(cm.estimates)

Treatment Effect Estimates: Matching

                     Est.       S.e.          z      P>|z|      [95% Conf. int.]
--------------------------------------------------------------------------------
           ATE      0.386      0.025     15.400      0.000      0.337      0.436
           ATC      0.377      0.028     13.683      0.000      0.323      0.431
           ATT      0.405      0.027     15.185      0.000      0.353      0.458

结果显示，ATE为0.38，这更符合我们之前在倾向得分加权方面看到的结果。在倾向得分匹配方面，我们也可以理解在处理组和未处理组之间的倾向得分有很小的重叠为什么是危险的。如果出现这种情况，倾向得分匹配差异将会很大，这将导致偏差，就像我们在匹配章节中看到的那样。

这里最后要注意的一点是，上述标准误差是错误的，因为它们没有考虑到倾向得分估计中的不确定性。不幸的是，bootstrap无法在匹配中使用。此外，上述倾向得分方法没有正确计算标准误差的Python实现。因此，我们在Python中没有看到很多倾向得分匹配。

小结

• 首先，我们了解到分配到处理组的概率称为倾向得分，我们可以将其用作平衡倾向得分。这意味着，如果我们有倾向得分，我们不需要直接控制混杂因素。仅控制倾向得分就足以确定因果效应。我们看到了倾向得分如何在混杂因素中起到降维作用。这些属性使我们能够推导出因果推断的加权估计器。不仅如此，我们还看到倾向得分可以与其他方法一起用于控制混杂偏差。

• 然后，我们看了一些常见的倾向得分和因果推断问题。第一个问题是，当我们沉迷于拟合处理机制时，提高处理的预测性能并不会转化为更好的因果估计，因为它可能会增加方差。

• 最后，我们看了一些可能会遇到的外推问题，如果我们不能在处理和未处理的倾向得分分布之间获得很好的重叠会产生什么后果。