3D Gaussian Splatting 数学原理与推导

置顶

scott198512

已于 2025-04-06 13:36:39 修改

阅读量1.5k

点赞数 19

分类专栏：三维重建新范式文章标签：计算机视觉图形渲染 3D重建高斯泼溅

于 2025-02-22 13:43:33 首次发布

本文链接：https://blog.csdn.net/scott198510/article/details/145793304

版权

引言

神经辐射场（NeRF）的出现，在新视图合成领域引起了广泛关注，显著提高了合成结果的质量。然而，NeRF 训练和渲染速度较慢，且训练结果为隐式表达的特性，这阻碍了它在 VR、AR、自动驾驶数据合成等行业的实际应用。

尽管文献中已经进行了大量尝试来加速这一过程，但要找到一种可靠的方法，既能在消费级 GPU 上快速训练 NeRF，又能在手机和笔记本电脑等普通设备上以交互式帧率渲染 3D 场景，仍然具有挑战性。2023 年在 SIGGRAPH 会议上由 Kerbl 等人提出的 3D 高斯泼溅（3DGS），成为了 NeRF 的一种更快替代方案，且合成质量相当，使低成本、实时的 3D 内容创作成为可能。

3D Gaussian Splatting源于EWA的理论基础，本文重点从EWA模型出发，详细推导3D GS中的数学原理，加深对鱼眼相机畸变场景下3D GS渲染结果的理解。

基于点的图形学

在众多计算机图形学应用中，（三角形）网格通常是最常见的表面表示形式，因为它们简单且灵活，任何形状和拓扑结构的表面都可以由单个网格集合来表示。然而，网格可能并不适合现代计算机，因为它们变得越来越复杂，而典型的屏幕分辨率却没有以相同的速度增长。

CPU 和图形硬件性能的飞速提升，以及高效的内存管理，使得处理大量高度详细的几何数据成为可能。因此，如今由数百万个网格组成的 3D 模型随处可见。当三角形的数量超过屏幕上可容纳的像素数量时，渲染如此庞大的数据集会变得极其低效，因为那些在屏幕上投影面积小于一个像素的三角形会造成资源浪费。

图 1. 硬件GeForce4 每秒能够处理 1.36 亿个顶点(资料1）

在这一快速发展的背景下，研究人员开始探索替代的几何基元 (geometric primitives)。1985 年由 Levoy 和 Whitted 首次提出的基于点的渲染，由于 Levoy 等人在 2002 年 SIGGRAPH 会议上发表的题为《数字米开朗基罗项目：大型雕像的 3D 扫描》的工作而重新受到关注。

图 2. 3D雕塑高质量的扫描结果

表面元素（Surfel）：点样本属性

基于点的渲染可以被理解为从点样本进行表面重建：给定一组点，渲染算法旨在将其转换为一个平滑的表面。

每个点样本由其位置、表面法线以及对应表面点的颜色等着色属性来表征。如果给点样本分配一个面积，即把一个表面点看作一个圆盘，在基于点的渲染领域中，它被称为表面元素（surface element），简称为 surfel。直观地说，surfel 的面积必须完全覆盖表面，以确保重建出无孔洞的表面。

图 3. Surfel 属性

点渲染管线

与光栅化类似，点渲染管线按如下步骤处理点数据：

正向扭曲（Forward Warping）：这一阶段使用透视投影将每个点投影到屏幕空间。这类似于将三角形顶点投影到图像空间。
着色（Shading）：进行逐点着色，任何局部着色模型都适用。着色通常在可见性处理之后（仅对可见点进行着色），或者在使用插值点属性进行图像重建之后（逐像素着色）进行。
可见性与重建（Visibility & Reconstruction）：这两个阶段在屏幕空间中形成与视图相关的表面重建，类似于三角形光栅化。

图 4. 点的渲染管线

泼溅（Splatting）

在传统文献中，已经探索了多种从 surfel 到图像的重建算法，泼溅是最常见的重建方法之一。该方法假设在物体空间中为每个 surfel 分配一个表面区域，并通过逼近 surfel 的投影来重建连续表面。投影后的 surfel 所形成的形状被称为 splat。

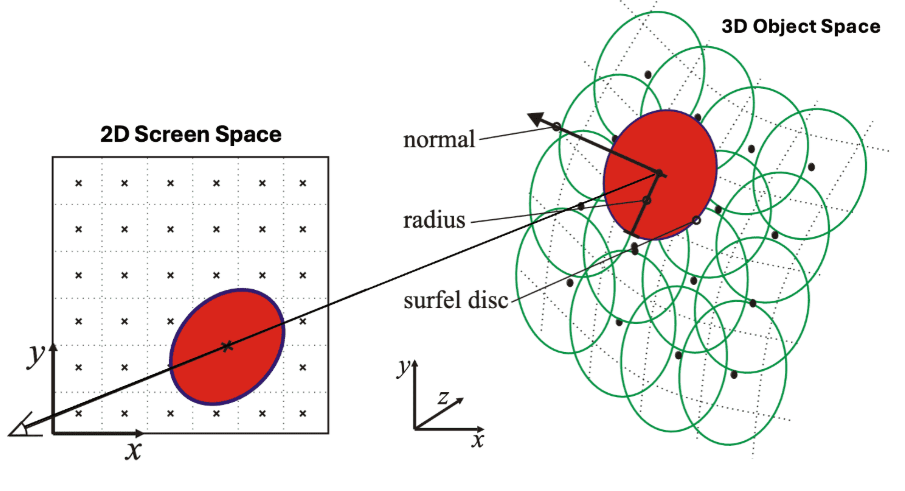
图 5. 泼溅的可视化

然而，如上图所示，简单地渲染相互穿透的 splat 会导致着色不连续，因此高质量的泼溅需要仔细分析混叠问题。Zwicker 等人在 2001 年的 SIGGRAPH 会议上提出了一种高质量的抗混叠方法，称为表面泼溅，它类似于 Heckbert 的 EWA 纹理过滤。

图 6. 泼溅和着色的比较。朴素泼溅（左中）、使用 Gouraud 着色的插值（右中）、使用 Phong shading的插值（右）

表面泼溅

表面泼溅的概念主要基于信号处理理论，特别是基于局部加权平均滤波对非均匀采样的函数或信号进行连续重建。

信号处理理论对均匀采样的函数或信号的连续重建有很好的理解和描述。首先从原始函数 $f$ 得到均匀采样函数或信号，

$\tilde{f}(x) = \sum_{i = 1}^n f(i) \delta(x - i)$

通过将采样信号与重建滤波器卷积来实现连续重建，卷积kernel为 $h$ ，即重建信号可以通过下述得到。即：

$g(x) = (\tilde{f} \otimes h^{1/2}) (x)=\sum_{i=1}^n f(i) h^{1/2} (x-i)$

然而，信号处理理论并不适用于非均匀采样，处理起来也较为复杂。在这种情况下，可以通过构建重建kernel 函数 $r$ 的加权和来重建连续信号，类似于均匀采样的情况：

$g(x) = \sum_{i=1}^n f(x_i) r_i (x - x_i) / \sum_{j=1}^n r_j (x - x_j)$

图 7. 信号处理理论中的连续重建

直观地说，表面可以被看作是高维空间中的低维信号。通过 3D 物体空间中的离散采样点，每个点在其局部坐标中封装了连续纹理函数（对应于重建核）的表示，表面泼溅旨在在 2D 图像空间中重建一个连续表面。重建是通过在图像空间中计算重建核的加权和来完成的。

图 8. 参数化信号重建与表面泼溅之间的等效性

此外，为了避免混叠伪影，表面泼溅采用了带预滤波的重采样概念，这一概念由 Paul Heckbert 在 1989 年引入计算机图形学，用于纹理过滤和图像扭曲。重采样包括以下步骤：

在源空间（对应于参数空间）中重建连续信号。
将连续信号扭曲到目标空间（对应于屏幕空间）。
应用预滤波器去除扭曲信号中的高频成分，即对信号进行带限(band-limit)处理。
在目标空间的新采样网格上对带限信号进行采样，避免任何混叠伪影。

表面纹理的 2D 参数化

设点采样表面是三维物体空间中一组没有连接关系的不规则分布点 ${ \mathbf{p}_k }$ 。点具有相应的位置和表面法线，每个点 ${ \mathbf{p}_k }$ 都与一个基函数 $r_k$ 以及颜色通道的系数 $w_k^r, w_k^g, w_k^b$ 相关联。不失一般性，这里仅以单个通道 $w_k$ 进行讨论。由于 3D 点通常是不规则分布的，因此简单采用径向对称基函数的加权和。对于给定的表面上的点 $\mathbf{q}$ ，具有局部坐标（即在局部参数化的坐标系）为 $\mathbf{u}$ ，连续纹理函数的值表示为，

$f_c (\mathbf{u}) = \sum_{k \in \mathbb{N}} w_k r_k (\mathbf{u} - \mathbf{u}_k)$

其中 $\mathbf{u_k}$ 是点 $\mathbf{p_k}$ 的局部坐标。

图 9. 在基于点的物体表面上定义纹理函数

纹理映射到屏幕

有了上述这个模型，就可以将基于点的物体渲染任务视为对连续纹理函数进行扭曲、滤波和采样的串联过程，如图 11 所示。用 $\mathbf{x} = \mathbf{m}(\mathbf{u})$ 表示从 2D 参数化空间到 2D 屏幕空间的映射。那么，渲染包括以下三个步骤：

1. 扭曲到屏幕空间：

$g_c (\mathbf{x}) = (f_c \circ \mathbf{m}^{-1}) (\mathbf{x})=f_c(\mathbf{m}^{-1} (\mathbf{x}))$

其中， $\circ$ 表示函数的级联，那么，由 $\mathbf{x} = \mathbf{m}(\mathbf{u})$ 得到 $\mathbf{u} = \mathbf{m}^{-1}(\mathbf{x})$ .

2. 滤波：为了抗混叠，使用预滤波器prefilter $h$ 对屏幕空间信号进行带限处理，以防止超过奈奎斯特准则（pre 表示在离散化显示之前），其中 $h$ 也就是卷积核，最终得到连续输出函数：

$g_c' (\mathbf{x})= g_c (\mathbf{x}) \otimes h(\mathbf{x}) = \int_{\mathbb{R}^2} g_c (\xi) h(\mathbf{x} - \xi) \mathrm{d} \xi$

那么， $g_c' (\mathbf{x})$ 的显式表达式可以推导如下：

$\begin{aligned} g_c' (\mathbf{x}) =\int_{\mathbb{R}^2} h(\mathbf{x}-\xi) \sum_{k \in \mathbb{N}} w_k r_k\left(\mathbf{m}^{-1}(\xi)-\mathbf{u}_k\right) \mathrm{d} \xi =\sum_{k \in \mathbb{N}} w_k \rho_k(\mathbf{x}) \\ \text { where, } \rho_k(\mathbf{x})=\int_{\mathbb{R}^2} h(\mathbf{x}-\xi) r_k\left(\mathbf{m}^{-1}(\xi)-\mathbf{u}_k\right) \mathrm{d} \xi \end{aligned}$

这里，经过扭曲和滤波的基函数 $\rho_k (\mathbf{x})$ 被称为重采样kernel。这个公式表明，可以先分别对每个基函数 $r_k$ 进行扭曲和滤波，构建重采样核 $\rho_k$ ，然后在屏幕空间中汇总这些核的贡献。如前所述，在这种情况下，对基函数的扭曲操作与将 surfel 投影到屏幕空间的操作是一致的。因此，作者将这种方法称为表面泼溅：

图 10. 通过表面泼溅进行渲染

为了简化 $\rho_k$ 的积分运算，在点 ${\mathbf{u}_k}$ 附近定义物体到屏幕映射的仿射近似 $\mathbf{m}_{\mathbf{u}_k}$ ，其中， $\mathbf{J}_{\mathbf{u}_{\mathbf{k}}}$ 表示雅可比矩阵。

$\begin{gathered} \mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u})=\mathbf{x}_{\mathbf{k}}+\mathbf{J}_{\mathbf{u}_{\mathbf{k}}} \cdot\left(\mathbf{u}-\mathbf{u}_{\mathbf{k}}\right) \\ \text{ where } \mathbf{x}_{\mathbf{k}}=\mathbf{m}\left(\mathbf{u}_{\mathbf{k}}\right) \text{ and the Jacobian } \left. \mathbf{J}_{\mathbf{u}_{\mathbf{k}}}=\frac{\partial \mathbf{m}}{\partial \mathbf{u}} \right\vert_{\mathbf{u} = \mathbf{u}_{\mathbf{k}}} \end{gathered}$

那么， $\rho_k$ 可以简化为，

$\begin{aligned} \rho_k(\mathbf{x}) =\int_{\mathbb{R}^2} h\left(\mathbf{x}-\mathbf{m}_{\mathbf{u}_k}\left(\mathbf{u}_k\right)-\xi\right) r_k^{\prime}(\xi) \mathrm{d} \xi =\left(r_k^{\prime} \otimes h\right)\left(\mathbf{x}-\mathbf{m}_{\mathbf{u}_k}\left(\mathbf{u}_k\right)\right) \end{aligned}$

其中，

$r_k^\prime (\mathbf{x}) = r_k (\mathbf{J}_{\mathbf{u}_{\mathbf{k}}}^{-1} \mathbf{x})$

此处推导 $\rho_k (\mathbf{x})$ 的简化过程：

$\rho_k(\mathbf{x})=\int_{\mathbb{R}^2} h(\mathbf{x}-\xi) r_k\left(\mathbf{m}^{-1}(\xi)-\mathbf{u}_k\right) \mathrm{d} \xi$

由上文可知，在局部小邻域内使用仿射变换 $\mathbf{m}_{\mathbf{u}_k}$ 近似投影变换 $\mathbf{m}$ 合理，那么

$\mathbf{u} = \mathbf{m}^{-1}(\mathbf{\xi})\approx \mathbf{m}_{\mathbf{u}_{\mathbf{k}}}^{-1}(\xi)\\\\ \mathbf{m}({\mathbf{u}_k})\approx\mathbf{m}_{\mathbf{u}_k}({\mathbf{u}_k})$

由此得到：

$\xi= \mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u})$ ,

再由 $\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u})=\mathbf{x}_{\mathbf{k}}+\mathbf{J}_{\mathbf{u}_{\mathbf{k}}} \cdot\left(\mathbf{u}-\mathbf{u}_{\mathbf{k}}\right)$ 得到： $\mathrm{d} \xi=|\mathbf{J}_{\mathbf{u}_{\mathbf{k}}} |\mathrm{d} \mathbf{u}$ ，从而带入：

$\begin{aligned} \rho_k(\mathbf{x}) &=\int_{\mathbb{R}^2} h(\mathbf{x}-\xi) r_k\left(\mathbf{m}^{-1}(\xi)-\mathbf{u}_k\right) \mathrm{d} \xi \\ &=\int_{\mathbb{R}^2} h(\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u})) r_k\left(\mathbf{u}-\mathbf{u}_k\right) |\mathbf{J}_{\mathbf{u}_{\mathbf{k}}} |\mathrm{d} \mathbf{u} \\ \end{aligned}$

再根据定义式 $r_k^\prime (\mathbf{x}) = r_k (\mathbf{J}_{\mathbf{u}_{\mathbf{k}}}^{-1} \mathbf{x})$ 得到：

$r_k^{\prime}(\mathbf{J}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u}-\mathbf{u}_k))=r_k(\mathbf{u}-\mathbf{u}_k)$

代入后得到：

$\rho_k(\mathbf{x}) =\int_{\mathbb{R}^2} h(\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u})) r_k^{\prime}(\mathbf{J}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u}-\mathbf{u}_k)) |\mathbf{J}_{\mathbf{u}_{\mathbf{k}}} |\mathrm{d} \mathbf{u}$

根据卷积的定义：

$(f\otimes g) (t)=\int_{\mathbb{R}^2} f(s)g(t-s)ds$

令 :

$s=\mathbf{J}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u}-\mathbf{u}_k)\\\\ t=\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u_k})$

那么

$\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u})=\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u_k})-\mathbf{J}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u}-\mathbf{u}_k)=\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u_k})-s$

$\begin{aligned} \rho_k(\mathbf{x}) &=\int_{\mathbb{R}^2} h(\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u_k})-s) r_k^{\prime}(s)|\mathrm{d} s \quad\quad\quad\quad (s\rightarrow \xi ) \\ &=\int_{\mathbb{R}^2} h(\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u_k})-\xi) r_k^{\prime}(\xi)|\mathrm{d} \xi \\ &= (r_k^{\prime} \otimes h)(\mathbf{x}-\mathbf{m}_{\mathbf{u}_{\mathbf{k}}}(\mathbf{u_k})) \end{aligned}$