对抗攻击(1)

本文是根据李宏毅老师在B站上的视频整理而来，视频地址为：
https://www.bilibili.com/video/BV1n3411y7xD?p=65

1 无目标和有目标攻击的区别

无目标攻击：攻击后的标签不确定，只要是和原始标签差别越大越好。
有目标攻击：攻击后的标签是确定的某一个类别，并且要求和原始标签差别越大越好。

图1说明了如何将对抗攻击转换为优化目标函数。
$x^{\ast }=\arg {\min }_{d(x^0,x)\le \epsilon }L(x)$：约束条件是原始样本和攻击样本之间差距很小（小于等于$\epsilon$），在损失最小的情况下得到攻击样本；
$L(x)=-e(y,\hat{y})$：应用于无目标的攻击，攻击后的预测标签和原始标签的差别越大越好，前面加一个负号就是越小越好；
$L(x)=-e(y,\hat{y})+e(y,y^{target})$：应用于有目标的攻击，攻击后的预测标签和原始标签的差别越大越好，并且攻击后的预测标签和被攻击的目标标签差距越小越好。

符号说明：
$x^0$：原始样本；
$x$：攻击样本；
$y^0$：没有受到攻击的预测标签；
$\hat{y}$：原始标签；
$y$：攻击后的预测标签；
$y^{target}$：有目标攻击的目标标签；
$y^0=f(x^0)$：利用原始样本预测出标签；
$y=f(x)$：利用受攻击后的样本预测出新的标签；

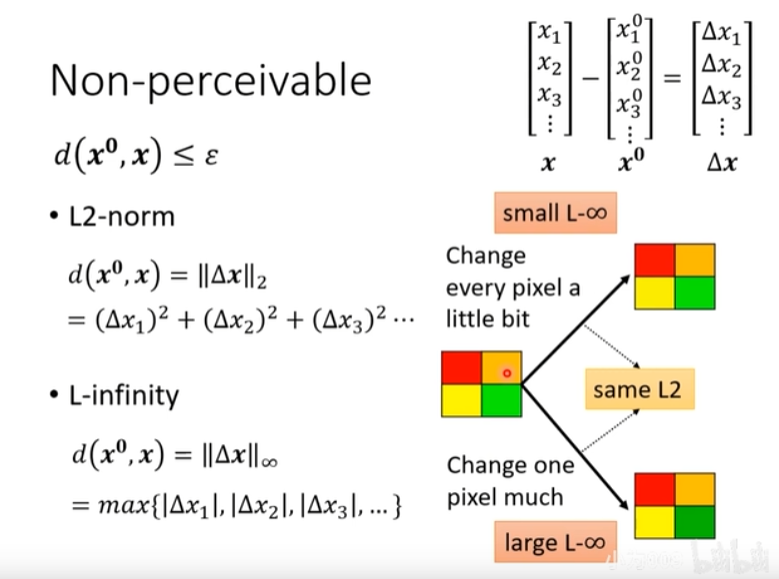
图2说明了如何来度量原始样本$x^0$和攻击样本$x$之间的距离：

1. 利用2范数来度量：
   $$\begin{array}{rl}d(x^0,x)& =||\Delta x|{|}_2\\ & =(\Delta x_1{)}^2+(\Delta x_2{)}^2+\dots \end{array}$$
2. 利用无穷范数来度量：
   d ( x 0 , x ) = ∣ ∣ Δ x ∣ ∣ ∞ = max ⁡ { ∣ Δ x 1 ∣ , ∣ Δ x 2 ∣ , …   } \begin{aligned} d(x^0,x) &= ||\Delta x||_\infty \\ &=\max\{|\Delta x_1|, |\Delta x_2|, \dots\} \end{aligned} d(x0,x)​=∣∣Δx∣∣∞​=max{∣Δx1​∣,∣Δx2​∣,…}​

通过如下分析来体会两个距离的最大区别：
一种情况是图像中的每个像素点都改变一点点，另外一种情况是图像中某一个像素点改变特别大；这两种情况也许2范数距离相同，但是无穷范数第一种情况很小，而第二种情况却很大。

图3说明了攻击方法不是去修改模型的参数，而是修改输入的样本。
可以从两个方面入手进行攻击：

• 修改优化目标函数
• 修改约束条件

最后利用梯度下降法来求得攻击样本$x$。
在迭代的时候如果$d(x^0,x^t)>\epsilon$，则将$x^t$拉回到矩形框内。

图4说明了FGSM方法。
对图3做了如下改进：

• 用$\epsilon$替换学习率$\eta$；
• 梯度$g$用$sign$函数来控制，使得其值为+1或者-1，也就是每次变化移动到矩形框四个角的某一个；
• 只需要迭代一次。
  

图5在图4的基础上又做了如下改进：

• 将图4的学习率又从$\epsilon$改回$\eta$;
• 通过$T$次迭代；
• 每次迭代如果$d(x^0,x^t)>\epsilon$，则将$x^t$拉回到矩形框内。
  

以上攻击方法都属于白盒攻击，因为攻击者知道网络参数$\theta$。
图6引入了黑盒攻击。

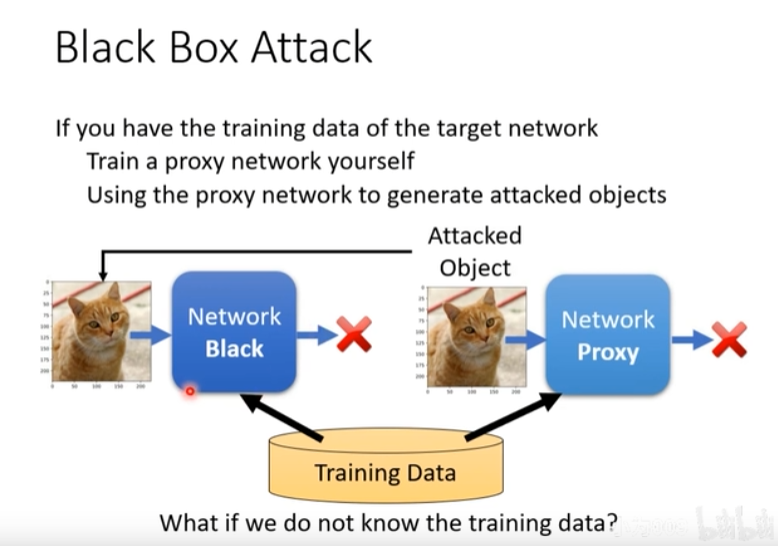
图7说明了黑盒攻击方法：如果你知道目标网络的训练数据，可以利用这些数据训练出一个代理网络(proxy network)，再利用这个代理网络产生攻击样本。
问：如果又不知道训练数据怎么办？
答：利用已有的黑盒模型，输入一些测试样本，得到测试样本的输出，利用这些输入和输出来训练一个代理网络(proxy network)，再利用这个代理网络产生攻击样本。

图8说明黑盒攻击的效果。
上半部分表示单一网络攻击的效果，对角线表示白盒攻击，例如ResNet-152攻击ResNet-152；非对角线表示黑盒攻击，例如ResNet-152攻击ResNet-101；攻击后的准确率越低，说明攻击成功率就越高，如ResNet-152攻击ResNet-101后得到的准确率为13%。
下半部分表示集成网络攻击的效果，如-ResNet-152表示由(ResNet-101 + ResNet-50 + VGG-16 + GoogleNet)这四个网络来集成。可以看出集成攻击的效果更好。