CPT205 Computer Graphics 计算机图形学 Pt.1（含OpenGL）

1.Introduction

1.1 What is Computer graphics?（什么是计算机图形学？）

‘Computer Graphics’ is concerned with all aspects of producing pictures or images using a computer.It includes three parts:1.The images that you see on the computer screen. 2.The computer code that is used to create the images. 3. A mathematical model of the real-world(which is sometimes called the virtual world).

计算机图形学是关于电脑创建图片或图像的所有方面，包含三个部分：1.电脑屏幕上你看到的图像。2,电脑用于生成图像的代码。3.关于显示世界的数学模型，它有时可以被理解成虚拟世界。

应用方向包括：1.Display of information（信息显示）。 2.Design（设计）。3. Simulation/modelling and animation（方针、建模和动画）。4.User interfaces（用户界面）。5.Virtual reality（虚拟现实）。

基础概念：
1.Graphics hardware and software
2.Fundamental mathmatics
3.Objects / geometric primitives --point,curve,surface and solids
4.Modelling and represenation schemes
5.Geometric transformations
6.Viewing and projections
7.Clipping
8.Removal of hidden curves and surfaces
9.Litghting and materials
10.Texture mapping
11.Animation
12.Programming and applications

1.2 Hardware and Software（硬件和软件）

硬件包括1.输入、处理、输出设备 2.Framebuffers，显存的一部分）3. Pixels and Screen Resolution(像素和屏幕分辨率）
软件包括 1.算法和程序 2.编程库/API （OpenGL，JOGL and so on) 3.高级交互系统（Maya, Studio Max, Unity, AutoCAD and so on)

1.2.1 Graphic hardwares（图形硬件）

1.2.1.1 Output devices（输出设备）

日常：
CRT屏（阴极射线管显示屏，显示器使用电子枪发射电子束，通过控制电子束的位置和强度来在荧光屏上生成图像。现如今逐渐被淘汰）
LCD屏（液晶显示屏，显示器由像素构成，每个像素包含红蓝绿三种液晶单元，通过控制液晶单元的透明度和颜色从而呈现图像）
投影桌

VR：
Head-Mounted Displays（HMDs）：头戴式显示设备。
Head-Tracked Displays（HTDS）：通过追踪用户的头部呈现对应图像从而避免了限于戴在头部。Example:CAVE,Workbench,Stereo monitor

1.2.1.2 Processing devices（处理设备）

Graphics Cards/GPU

1.2.1.3 Input devices（输入设备）

需要进行图形交互所以他需要确定位置/方向，因此比如Tablets,Virtual Reality Trackers, Light Pens, Voice Systems, Touch Pannels, Camera/Vision based, some game devices…

1.2.1.4 Framebuffer（帧缓冲区）

帧缓冲区是用于储存图像数据的内存区域，通常用于存储将要在屏幕上显示的图像。它的组成元素是Pixel（像素），它储存了屏幕上每个像素的颜色值。
换句话说，framebuffer中的数据描述了屏幕上每个像素的颜色，这些数据代表的颜色在屏幕上被显示出来就形成了图像。

因此我们在OpenGL里修改的正是Framebuffer，最后我们绘制完毕后将Framebuffer的结果输出出来就成了我们要的图像。

从前面的定义我们可以看出如果我们的电脑显示屏上的像素点越多我们需要的Framebuffer的空间也越大，而且我们如果只用0或1去表示一个像素点我们只能表示这个像素点亮与不亮，我们需要更多的信息去表示一个像素点该呈什么颜色——因此我们有bit depth（位深度）来表示每个像素所占用的位数。
我们一般使用RGBA，三原色RGB加上透明度Alpha，每个都用8bits一共32bits来满足我们对像素点可以展示任意颜色的需求。

framebuffer bit depths 的例子如下：

因此Graphic card memory（显存）越大才能呈现出更多的像素点，比如1600*1200像素点的显示区域还需要32bits一共是1600*1200*32bits = 7,680,000bytes。

当这些数字值需要显示在显示器上时，它们会被转换成模拟信号。当这些数字值需要显示在显示器上时，它们会被转换成模拟信号。而且转换可以在写入帧缓冲区的同时进行。

1.2.1.5 Image quality issues（图像质量问题）

1.Screen resolution（分辨率）
2.Color（颜色）
3.Refresh rate（刷新率）
4.Brightness（亮度）
5.Contrast（对比度）
6.Sensitivty of display to viewing angle（显示器对观看角度的敏感度）（侧着观看屏幕时对图像的亮度、对比度、颜色等产生变化）

1.2.1.6 Pixels（像素）

The most basic addressable image element in a screen(屏幕上的最基础可寻址的元素)
CRT上每个像素由三原色的磷光点组成，当电子束扫描到屏幕上的特定位置时，它会激发红色、绿色和蓝色的磷光点，通过控制这些磷光点的激发强度和位置呈现图像。
LCD上每个像素由三原色的sub-pixels(单色元素)组成,通过对单色元素的排列和控制呈现图像。

屏幕分辨率指水平方向的像素点数乘以竖直方向的像素点数

1.2.1.7 Video formats（视频格式）

1.NTSC - 525x480, 30f/s, interlaced
2.PAL - 625x480, 25f/s, interlaced
3.VGA - 640x480, 60f/s, non-interlaced
4.SVGA - 800x600, 60f/s non-interlaced
Interlaced（隔行扫描）通过交替扫描屏幕的偶数和奇数行来呈现图像。
视频帧被分为两个字段，偶数行为一个字段，奇数行为另一个字段。首先显示偶数行的字段，然后立即显示奇数行的字段，这样就完成了一帧图像的显示。

1.2.1.8 Raster display

Cathode Ray Tubes(CRTs)：显示器使用电子枪发射电子束，通过控制电子束的位置和强度来在荧光屏上生成图像。
特点：1.强电场和高压（因为需要驱动电子束运动）
2.高分辨率
3.重且不平坦

Liquid Crystal Displays(LCDs)原理可以看：https://www.bilibili.com/video/BV1Wz411B7Tf/?spm_id_from=333.337.search-card.all.click&vd_source=3e562ebba9d60af0c036a8e95b29f3c1
由于原理不同所以LCD会受观看角度的影响。

特点：1.平坦
2.轻量化
3.低能源消耗

1.2.2 Graphics software（图形软件）

软件包含了：
1.Graphics drivers（图形驱动）
2.Graphics libraries（图形库）
3.Graphics editors（图形编辑器）
4.Gemetric modellers（几何建模器）
5.VR modellers（VR建模器）
6.Games（游戏）
7.Scientific visualisation packages（科学可视化包）

软件让我们可以更方便控制前面我们说的硬件，本课聚焦的将是OpenGL。

2.Maths(与该课程相关的一些基础数学知识）

2.1 Computer representation of objects（计算机对物体的呈现）

1. 3D points of objects → Manipulation of 3D points → Display of points on 2D screen
2. Model of 3D world → Transformation → Projection
3. Storage → Calculation → Display

这三个是三种不同层次，我们OpenGL的操作主要是第二个先建模再对这个建模后的3D物体进行变换操作从而改变物体的空间位置和方向，再通过投影将这个3D物体投影到2D屏幕上，从而显示出来。而第三个可以理解成硬件中存储的数据通过处理器的计算最后显示到输出设备上。

2.2 Cartesian co-ordinate system

因此比如以下的代码。

#define FREEGLUT_STATIC // Define a static library for calling functions 
#include <GL/freeglut.h> // Include the header file 

void renderScene(void) // Function for geometric creation
{
	// Clear the buffer to the predefined color and depth value 
	glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
	//Move origin of current user coordinate system to the screen center: similar to a reset operation 
	glLoadIdentity();
	glBegin(GL_TRIANGLES); // Start draw TRIANGLE function 
	glVertex3f(-0.5, -0.5, 0.0); // Set coordinates of first vertex 
	glVertex3f(0.5, 0.0, 0.0); // Set coordinates of second vertex 
	glVertex3f(0.0, 0.5, 0.0); // Set coordinates of last vertex 
	glEnd(); // End draw TRIANGLE function 
	glutSwapBuffers(); // Refresh the screen to display the graphics 
}

int main(int argc, char* argv[]) // Standard main function 
{
	glutInit(&argc, (char**)argv); // Initialization 
	// Define display mode: depth buffer, double buffer and RGBA color 
	glutInitDisplayMode(GLUT_DEPTH | GLUT_DOUBLE | GLUT_RGBA);
	glutInitWindowPosition(100, 100); // Define the location of the window 
	glutInitWindowSize(320, 320); // Define the size of the window 
	glutCreateWindow("Hello OpenGL"); // Create a window called “Hello OpenGL” 
	glutDisplayFunc(renderScene); // Set the first function 
	glutMainLoop(); // Enter the GLUT event processing loop 
	return 0; // Return an integer value 
}

如果我们将glutInitWindowPosition(100, 100);修改成glutInitWindowPosition(100, 500);窗口是会往下而不是向上。

2.3 Points,lines and angles

不多赘述。

2.4 Trigonometry

不多赘述。

2,5 Vectors

注意区分点乘和叉乘。
dot product（点乘）：$V_1•V_2=x_1\ast x_2+y_1\ast y_2$
$V_1•V_2=|V_1||V_2|cos(\alpha )$
所以$cos(\alpha )=V_1•V_2/（|V_1||V_2|）$这里$\alpha$是$V_1$和$V_2$之间的夹角，$0\le \alpha \le 80^{\circ }$

cross product（叉乘）：$V_1\times V_2=|V_1||V_2|sin(\alpha )n$这里$\alpha$是$V_1$和$V_2$之间的夹角，$0\le \alpha \le 80^{\circ }$，$n$是$V_1$和$V_2$所在平面的法向量的单位向量，这是由右手定则来确定的。
所以$V_1\times V_2=-V_2\times V_1$

2.6 Matrices

不再赘述。

3.Geometric Primitives(组成图形的基本元素——几何图元）

图形是千变万化的，但它们都是有元素组成的，这些元素就是几何图元。

前面说到我们图形的输出设备是显示屏，显示屏是一个大型的像素点矩阵，而我们在这个上面显示图形要经过一个Rasterization（光栅化）的过程。
光栅化指的是将各种图形转化为屏幕上离散的像素点的过程。这里的图形也可以是3D物体投影到2D平面上的2D图像。
光栅化中，计算机会根据图形的位置、大小、形状等信息确定每个图元的像素点位置，从而呈现最后的图形。

3.1 Graphics Primitives

点、线、多边形。

3.2 Line Algorithms

刚刚我们说到了图元有哪些，但是如何在像素点构成的屏幕上画一条好的线呢？
我们有以下几点要求：线是连着的没有断开，与我们理想的线接近，足够光滑，在同样情况下是一样的，比如从p1到p2的直线和p2到p1的直线一样，在所有方向亮度均匀…

比如我们画一个水平或者竖直的线很容易，但是如果一个线是斜着的，那我们需要一些算法来解决这样的问题。

3.2.1 DDA —— Digital Differential Algorithm

它是一种增量式扫描算法（通过逐步增加x坐标或y坐标的整数部分，来确定线段在屏幕上的像素位置）（确定到底是逐步增加哪个坐标可以判断x和y谁的变化量大谁就是自变量或者说叫步进方向）。
核心思想：先判断x和y谁的变化量大，以它为自变量，计算因变量的值，四舍五入从而确定像素点。
如果我们这里是x的变化量大，那我们就以x为自变量，沿着x轴方向每次增加x，确定y的像素点。
所以当$0\le |m|\le 1$时，$∆x=1，∆y=m$,算法如下：

int x;
float y=y1;
for(x=x1; x<=x2; x++){
	write_pixel(x, round(y), line_color);
	y+=m;
}

如图所示，假设画一个P1到P2的直线，x变化量更大，所以x作为自变量，x=0的时候y=0所以第一个像素点是（0，0），x=1的时候y=3/4所以第二个像素点是（0，1），x=2的时候y=6/4所以第二个像素点是（2，2），x=3的时候y=9/4所以第三个像素点是（3，2），x=4的时候y=3所以第四个像素点是（4，3）。

如图所示，左边的直线是y的变化量大于x的变化量的，此时以y作为自变量，计算x再四舍五入。当然你也可以理解成斜率的绝对值大于1。而右边的直线则是斜率的绝对值在0到1之间是x的变化量大于y的变化量的，做法和前文一致。

这里代码只支持x作为自变量且输入的x坐标是整数情况（如果你输入的数过大也无法显现出来），示例如下：

#define FREEGLUT_STATIC
#include <GL/freeglut.h>
#include <math.h>
#include <iostream>

//DDA算法在x大于y的情况下且是整数

using namespace std;

int x11, x22;
float y11, y22;
float gradient;
void define_to_OpenGL();

int main(int argc, char** argv)
{
	cout << "Please input the x value for the first point:\n";
	cin >> x11;
	cout << "Please input the y value for the first point:\n";
	cin >> y11;
	cout << "Please input the x value for the second point:\n";
	cin >> x22;
	cout << "Please input the y value for the second point:\n";
	cin >> y22;
	glutInit(&argc, (char**)argv);
	glutInitDisplayMode(GLUT_DEPTH | GLUT_DOUBLE | GLUT_RGBA);
	glutInitWindowSize(600, 400);
	glutInitWindowPosition(50, 50);
	glutCreateWindow("Hello OpenGL");
	glutDisplayFunc(define_to_OpenGL);
	glutMainLoop();
}

void define_to_OpenGL() 
{
	glClear(GL_COLOR_BUFFER_BIT);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	gluOrtho2D(-5, 5, -5, 5);
	gradient = ((y22 - y11) / (x22 - x11));
	for (int x = x11; x <= x22; x++)
	{
		glPointSize(10);
		glColor3f(1, 0, 0);
		glBegin(GL_POINTS);
		glVertex2f(x, round(x * gradient));
		glEnd();
	}
	glutSwapBuffers();
}

输入数字0 0 3 4后应该获得如图结果：

和我们上面推测的结果一致。

3.2.2 The Bresenham line algorithm

也是一种增量式扫描转换算法，但是正确且高效，因为他只使用了整数计算而不像DDA需要浮点计算。

核心思想：将实际的线的落点与两个像素点的中点作比较，如果落点在中点的上方则取上面的像素点，如果落在中点的下方则取下面的像素点。

如图确定好x方向为步进方向后，判断实际落点（黑色的点）在中点（绿色点）的上方，所以取上面的像素点；下一个的实际落点在中点的下方，取下面的像素点。

那他如何做到只利用整数进行计算的呢？
它通过将误差项乘以2，并将所有计算保持在整数范围内来实现。

3.2.3 Generation of circles

刚刚说的算法都是直线，那圆形呢？
如果用传统的数学公式直接画圆形我们会得到这样的一个圆形。

由于当斜率的绝对值大于1的时候y值的变化比x值慢。所以导致这边的像素更密集，而斜率的绝对值在0到1之间的像素更疏松。

解决方案有几个：1.在斜率的绝对值大于1的时候用y作为自变量计算x。
2.用极坐标从而画出多个角度下的点，然后用直线将这些点连成线。

第二个方法比第一个方法在均匀程度上以及计算量都比方案一好很多，但是这样计算量依旧很大。

其实我们可以画0-45°的圆弧（这个区间的曲线的斜率绝对值等于或大于1），然后对称一次变成0-90°的圆弧，再对称一次变为0-180°的圆弧，再对称一次变成一个完整的圆。

3.2.4 Antialiasing by area averaging（面积平均法抗锯齿）

通过对像素覆盖的区域进行平均处理来减少锯齿状边缘的出现。

更多抗锯齿的信息可以看：https://www.bilibili.com/video/BV13z4y1K7CC/?spm_id_from=333.337.search-card.all.click&vd_source=3e562ebba9d60af0c036a8e95b29f3c1

3.2.5 Polygons and triangles

多边形是一系列顶点定义的。

一个复杂的物体可以被分割成三角形构成的多边形，这个过程被称为tessellation（镶嵌），能这么做的原因是因为它们都在一个平面上，三角形多边形是平面的。

3.3 Polygon Fill

计算机通过scan conversion（扫描转移）将三维空间的图形投影转换到二维空间。这个过程也叫做rasterization（光栅化）。这个过程会产生二维顶点，这些顶点可以确定二维图元。而在光栅化过程中，需要确定多边形内部的像素，并在帧缓冲区中填充这些像素。

3.3.1 多边形填充方法

3.3.1.1 递归填充算法

选择一个多边形内的点作为种子点，然后开始判断它相邻的点是否在多边形内从而递归循环，慢慢扩散。

3.3.1.2 扫描线填充算法

用水平的扫描线从上到下（或者从下到上）扫描多边形，计算扫描线与多边形的焦点，将交点按从小到大排序，然后将排序好的交点两两组成一个水平线段，以画线段的方式完成填充。

3.3.1.3 奇偶填充规则 （Odd-Even Fill Rule）

从任意位置p作一条射线，若与该射线相交的多边形边的数目是奇数则表示p是在在多边形内，是偶数则表示p在多边形外。
但是对于自相交的多边形，奇偶填充规则可能会出现问题。

3.3.2 多边形光照处理

3.3.2.1 Flat shading（平面着色）

每个多边形的整个表面都是一种颜色。

3.3.2.2 Smooth shading（平滑着色）

平滑着色考虑了多边形表面上不同点的发现，使得光照可以根据表面的曲率和发现的变化而产生变化。
换句话说不同的顶点颜色会让三角形的颜色有变化过渡。

3.4 Graphics Primitives with OpenGL

首先所有的图元类型写在glBegin()的括号中，glBegin()和glEnd()之间是图元的顶点位置。

GL_POINTS：就是点。
GL_LINES：输入两个顶点，将其连成线。（4个点就是2条线）
GL_LINE_STRIP：输入一系列点，前两个顶点连成线后，将这两个顶点的后一个与下一个顶点再连成线，循环到最后一个点为止。
GL_LINE_LOOP：跟前者相比最后一个点与第一个点再连成线。
GL_TRIANGLES：输入三个点画一个三角形。（6个点就是2个三角形）
GL_TRIANGLE_STRIP：输入一系列点，前三个点画一个三角形然后前一个三角形的后两个点和下一个点再一起画一个三角形，循环到最后一个点为止。
GL_TRIANGLE_FAN：输入一系列的点，后面的点都以第一个点为顶点画三角形。
GL_QUADS：输入四个点画一个四边形。（输入12个点就是3个四边形）
GL_QUAD_STRIP：输入一系列点，前四个点画一个四边形，然后这四个点的后两个点与接下来的两个点画一个四边形，循环到最后为止。
GL_POLYGON：输入一系列点连接这些顶点从而画一个多边形。

4.Transformation Pipeline and Geometric Transformations

我们在前面学习了计算机呈现物体的三个阶段Model of 3D world → Transformation → Projection，上一节中我们介绍了所有的物体都可以理解成由点、线、多边形组成的，这是建模阶段，当我们完成建模之后，我们只是构建了好了这个物体的模型，我们可能还要对它进行变换操作，这包含了平移、旋转、缩放等,经过这些变换操作之后模型才可能以我们想要的方式呈现。

补充：一个图像的生成包括了多个阶段：
1.建模阶段：一个物体的几何形状到底是什么样子，它还包括它的纹理和材质等信息
2.渲染管线阶段”模型经过模型变换、视图变换、投影变换等阶段从而将物体从局部坐标系变换到屏幕空间的像素坐标系中。这一阶段包含了Transformation（变换）和Projection（投影）这两个阶段。
3.光栅化阶段：前一步已经确定了像素坐标系，这一步便是确定将三维模型转换为二维像素。
4.片元着色阶段：对每个片元进行着色计算，包括光照、纹理、阴影等。
最后这些阶段处理后的图像呈现在屏幕上。

4.1 Transformation pipeline

如图所示，变换管线分为以下几个变换步骤，先是MC（Model Coordinate，模型坐标系）通过Modelling Transformation（模型变换）变换到WC（World Coordinate，世界坐标系），再通过Viewing Transformation（视图变换）变换到VC（Viewing Coordinate/Cammera Coordinate，相机坐标系），再通过Projection Transformation（投影变换）变换到PC（Projection Coordinate，投影坐标系），再通过Normaliazation Transformation and Clipping（标准化变换和裁剪）变换到NC（Normalization Coordinate，规范化坐标系），最后经过Viewport Transformation（视口变换）变换到DC（Device Coordinate，设备坐标系）。

OpenGL会在前两个变换中用Modelview matrix进行转换，接着的两个变换用Projection matrix进行转换。
Modelling Transformation是让模型在虚拟世界中有对应的坐标。
Viewing Transformation是从特定视角去观察物体。
Projection Transformation可以让我们感受到物体的深度。
Normalization Transformation是将物体以及前后裁剪平面映射到单位立方体中，从而方便后续操作。
Clipping是将视锥体之外的几何图形剔除，从而提高渲染效率。
Viewport Transformation是将规范化坐标里的图形映射到屏幕坐标系中的像素中。
设备坐标系指的是屏幕上的坐标系，其中每个点对应于屏幕上的一个像素，设备坐标系就是屏幕空间的像素坐标系。

也可以查看这张图。

详情还可以查看视频：https://www.bilibili.com/video/BV18t4y1c7fF/?spm_id_from=333.788&vd_source=3e562ebba9d60af0c036a8e95b29f3c1

4.2 Standard transformations

Rotation（旋转），Translation（平移），Scaling（缩放）不过多介绍。
Relfection（反射），它将图形沿着axis of reflection（反射轴）翻转。
Shearing（剪切），它将图形沿着某个方向拉伸或压缩，同时保持另一个方向不变的变换。二维的时候它可以是沿着x轴或y轴，三维的时候可以沿着x-z平面，y-z平面、x-z平面。但是它不是降维，比如一个正方体的一些面会在shearing的影响下变成平行四边形。

4.2.1 Transformation matrices

比较简单，这里不详细叙述。

注意：1.Rotation（旋转）其实是先将物体的旋转的中心点先放到原点，然后旋转这个物体，然后再将这个点还原到原来的位置，所以旋转的过程是一个复合变换，包含平移（T）、旋转（R）、再平移（T），因此 M = T(pf) R(q) T(-pf)。
2.Scaling（缩放）不仅改变大小，还会改变位置。
矩阵如下。

3.因此对于reflection（反射），各种情况如下。

4.Shearing（剪切）以沿着x轴方向剪切为例。
$x^{\prime }=x+ycot\theta ,y^{\prime }=y,z^{\prime }=z$
矩阵与示意图如下。

4.3 Homogeneous co-ordinate transformation matrices

将2x2矩阵扩展到3x3矩阵，可以使用homogeneous co0ordinates（齐次坐标）。
齐次坐标是一种表示二维点的方法，其中每个点由三个坐标组成，形式为$(h\cdot x,h\cdot y,h)$，其中$h$是一个非零的齐次参数,通常为了方便起见，可以设置为 1。
使用齐次坐标，所有的变换矩阵都可以统一为3x3矩阵的形式，包括平移矩阵。这使得不同类型的变换可以更容易地组合在一起。
所以现在各种transformation的矩阵如下：


因此2D composite transformation（二维复合变换）情况如下：

如图所示，该矩阵是将多种几何变换（旋转、缩放和平移）组合在一起的结果，
$rs$是旋转缩放在一起的结果，$trs$是平移的结果。

4.4 Composite(arbitrary) transformation matrices from simple transformations

首先我们将前面的二维拓展到三维中。
Translation（平移）：

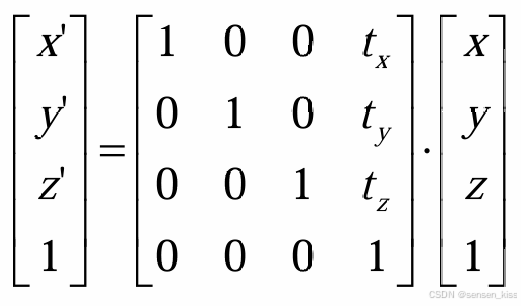
Rotation（旋转）：这里比较复杂，因为三维旋转是围绕一个任意轴进行的，而不是像二维旋转那样围绕一个点。在三维空间中，绕z轴的旋转可以看作是在所有z坐标相同的平面上进行的二维旋转。
因此关于z轴旋转的情况和原来的二维旋转类似：

关于y轴和x轴旋转的情况如下：

Scaling（缩放）：

注意：1.Rotation在三维空间中任意的旋转可以被拆解到x,y,z轴上。即$R(q)=R_z(q_z)R_y(q_y)R_x(q_x)$，表示一个旋转可以通过先绕x轴旋转$q_x$角度，然后绕y轴旋转$q_y$角度，最后绕z轴旋转$q_z$角度来实现（这里的角度都是欧拉角）。这里$R_x,R_y,R_z$分别代表绕x、y、z轴的旋转矩阵。
但是如果我们改变x,y,z轴的旋转顺序，我们需要改变对应的角度。换句话说旋转操作不满足交换律。
2.在三维空间中，我们可以使用矩阵相乘的方式来组合各种变换操作，从而形成复合的三维变换。（从这里也可以看出旋转不能交换顺序的原因）
3.Reflection和Shearing也可以用其他三种transformations来实现。
4.所有的transformations都是affine transformation（仿射变换），换句话说就是最后的点$P^{\prime }(x^{\prime },y^{\prime },z^{\prime })$是原来点$P(x,y,z)$的线性组合的结果。
5.由于是矩阵相乘的结果，所以它虽然不符合交换律，但是它符合结合律。
6.Instancing（实例化）可以让我们复用相同的几何模型，而采用不同的位置、旋转、缩放等变换以创建大量相似但不完全相同的对象。这种方法可以让我们以单个几何模型渲染多个相同的对象，从而节省内存和渲染时间。
如图所示，评估先进行了缩放，然后进行了旋转，然后进行了平移，从而创建了我们需要的对象实例。

4.5 OpenGL functions for transformations

前文说了OpenGL的底层用矩阵进行渲染的操作，因此矩阵是OpenGL的状态之一，而状态时渲染中的所有参数和属性的集合。也就是说我们改变矩阵的值就会影响最后渲染的结果。

这些矩阵包括：
1.Model-View (GL_MODELVIEW)
2.Projection (GL_PROJECTION)
3.Texture (GL_TEXTURE)
4.Color (GL_COLOR)

在实践中我们一般这么操作：

glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D(-100, 500, -200, 200);

上面的代码我们先将操作的对象改到了投影矩阵，然后将该矩阵改为单位矩阵（可以理解成清0），然后将投影矩阵的大小设置成了x轴从-100到500，y轴从-200到200。
注意：glMatrixMode默认是在处于model view矩阵，而不是投影矩阵，比如我们一般画图的时候我们画的图稍微大一点，最后结果不出现的原因就是我们没有修改投影矩阵。

对于当前的CTM（Cuurent Transformation Matrix，当前的变换矩阵，4x4的齐次坐标矩阵，通过修改这个矩阵从而控制图形的变换），我们可以通过加载一个新的变换矩阵或者对这个当前矩阵进行postmultiplication（后乘）操作从而改变当前变换矩阵。
在OpenGL中，有一个model-view matirx（模型-视图矩阵）和projection matrix（投影矩阵），这两个矩阵在pipeline（管道） 中被连接在一起形成CTM。在OpenGL中通过首先设置正确的矩阵模式来分别操作。
前面说到的两个操作在OpenGL分别是：（m代表Matrix）
1.glLoadMatrixf(m)
2.glMultMatrixf(m)

由于我们现实中可能需要回到之前的状态，也就是撤销上一步操作，这时候我们需要我们目前的CTM可以回到之前的transformation matrix，而stacks可以满足我们的需求（需求1.Traversing hierarchical data structures 遍历层次数据结构 2.Avoiding state changes when executing display lists 避免在执行显示列表时更改状态），因此实际中我们的CTM是matrix stack，而当前的状态正好在stack的top，我们想回到上一个状态我们只需要pop顶上的当前矩阵，我们就回到了前一个矩阵了。
因此openGL支持：glPushMatrix()和glPopMatrix()。
glGetIntegerv可以获取整数类型的OpenGL状态变量的值，例如堆栈的最大深度或当前堆栈中的矩阵数量。
它也使用查询函数来访问矩阵，方法有：
1.glGetIntegerv：获取整型状态变量的值。
2.glGetFloatv：获取单精度浮点型状态变量的值。
3.glGetBooleanv：获取布尔型状态变量的值。
4.glGetDoublev：获取双精度浮点型状态变量的值。
5.glIsEnabled：检查指定的capability是否启用。

所以一般我们使用
double m[16];
和
glGetFloatv(GL_MODELVIEW, m);

还有一些transformation的方法：
1.glTranslate
2.glRotate
3.glScale

指定当前矩阵的类型：glMatrixMode
加载还可以加载单位矩阵： glLoadIdentity
修改光栅化时2D缩放参数：glPixelZoom

前面这些方法比较简单，不详细叙述，这里提供一个例子，这个例子将位于（1，2，3）的点绕着z轴旋转了30度。

glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslatef(1.0, 2.0, 3.0);
glRotatef(30.0, 0.0, 0.0, 1.0);
glTranslatef(-1.0, -2.0, -3.0);

第一步将坐标原点移到(1.0, 2.0, 3.0)，从而将旋转中心移到(1.0, 2.0, 3.0)，第二步进行旋转，第三步还原坐标系的位置。
注意：最后指定的矩阵实际上是最先被应用的。
所以实现时先进行了最后一个平移，然后进行旋转，最后进行第一个平移。

5.Viewing and Projection

接上回讲完建模以及变换后，呈现物体的最后一步是Projection，也就是投影。但是说Projection也有个概念和其紧密相关，那就是Viewing（观察），viewing决定了观察的角度和位置，projection决定了观察者所看到的场景或物体在二维平面上的表现方式。换句话说没有viewing我们不知道projection该如何进行，没有projection我们也无法在viewing中看到物体的正确样子。

5.1 Concepts of viewing and projection

5.1.1 Classic viewing

Viewing（观察/视图）需要三个基本元素：
1.One or more objects（一个或多个对象）。
2. A viewer with a projection surface(一个具有投影平面的观察者）。
3. Projectors that go from the object(s) to the projection surface(从物体到投影平面的投影）。
经典的视图建立在这些要素之间的关系基础上。
观察者拿起物体并将其定位在要被观察的方式上。
每个物体都由平面主要面构成。
例如建筑物、多面体、制造的物体等。

5.1.2 Classic projection

先举几种projection方法抛砖引玉一下。

1.Front elevation(立面图）：是建筑或物体正面的图示。
2.Elevation oblique(斜侧图）：是一种展示物体外观的图示，与立面图相比观察角度是倾斜的。
3.Plan oblique(平面斜图）：类似于俯视图，但是观察角度是倾斜的，展示了物体在平面上的外观。
4.Isometric(等轴测图）：是一种三维图示方法，通过等比例地将物体的三个轴投影到一个平面上，展示物体的三维形状和结构。与数学的笛卡尔坐标系近似。
5.One-point perspective(一点透视）：是一种透视绘图方式，通过一个单一的消失点来表现三维空间在二维画面的效果。图中所有的线如果无限延展下去其实会在图的中间汇聚一点而消失。
6.Three-point perspective(三点透视）：是一种复杂的透视绘图方式，通过三个消失点来表现复杂的三维空间。

5.2 Types of projection and their advantages / disadvantages

5.2.1 Planar geometric projection(平面几何投影）

将三维物体投影到一个平面上的方法

投影线可以是从一个中心点（中心投影）发散出去的，也可以是平行的。
对于投影线从一个中心点发散出去，而这些投影线会汇聚到中心投影点上的这种投影方式叫Parallel（中心投影）或者Perspective（透视投影）。
对于投影线是平行的这种投影方式叫平行投影。

平面几何投影可以保存物体上的直线，但不一定能保存直线之间的夹角。

非平面几何投影在一些场景时也是必要的，比如地图制作的时候，地球是三维的球体，而地图时一个二维的平面，此时需要使用非平面几何投影。

5.2.2 Taxonomy of planar geometric projection（平面几何投影的分类）

由我们前面的一些概念我们也可以得出前面的那些投影之间的关系，如图：

按照投影线，我们将平面几何投影分成平行投影和中心投影（透视投影），其中我们按照消失点的数量将中心投影（透视投影）分成了One-point perspective(一点透视）、Two-point perspective(双点透视）、Three-point perspective(三点透视），将平行投影按照投影角度可以分为Multiview orthographic（多视图正投影）、Axonometric（轴侧投影）、Oblique（斜投影），其中Multiview orthographic（多视图正投影）下面又有包括主视图（front view）、俯视图（top view）和侧视图（side view），而Axonometric（轴侧投影）可以按照投影立方体的一个角的角度数量（各个坐标的长度比例和倾斜角度）又可以划分成Isometric（等轴测）、Dimetric（等角斜测）、Trimetric（等轴斜测）。
Isometric（等轴测）中所有三个坐标轴的长度比例相等，它们都与投影平面的夹角为120度，Dimetric（等角斜测）中两个坐标轴的长度比例相等，Trimetric（等轴斜测）中三个坐标轴的长度比例都不相等。

在计算机图形学中，所有投影都以相同的方式处理，并使用单一的管道来实现它们。
而在经典的视图方式中，针对每种类型的投影都发展了不同的绘制技术。
基本的区别在于透视视图和平行视图，尽管在数学上，平行视图是透视视图的极限情况。

5.2.3 Perspective projection（透视投影）

Perspective projection generates a view of 3- dimensional scene by projecting points to the view plane along converging paths（透视投影通过沿会聚路径将点投影到视图平面来生成三维场景的视图）。
因此它符合现实物理中的近大远小，也因为这一点，它比平行投影看上去更真实。

5.2.3.1 Perspective projection（透视投影）

投影线汇聚于投影中心（CoP）。

优点：1.符合近大远小，因此更真实。
2.非均匀缩短（也是近大远小）。

缺点：1.只有平行于投影平面的角才可以保存下来。
2.人们相较于平行投影难以画出透视投影（但是对于计算机不难）。

5.2.3.2 Vanishing points（消失点）

CoP（center of projection，投影中心）通常又被称为vanishing point（消失点），是指在透视投影中，物体上的平行线会在远离观察者的方向上汇聚到一个点上。

5.2.3.3 Three-point perspective（三点透视）

没有主要面平行于投影平面。
有三个消失点。

5.2.3.4 Two-point perspective（双点透视）

一个主要方向平行于投影平面。
有两个消失点。

5.2.3.5 One-point perspective（一点透视）

一个主要平面平行于投影平面。
有一个消失点。

5.2.4 Parallel projection（平行投影）

This method projects points on the object surface along parallel lines（此方法沿平行线在对象平面投影点）。

5.2.4.1 Orthographic projection（正投影）

投影线与投影平面正交。

5.2.4.2 Multiview orthographic projection（多视图正投影）

投影平面平行于主面。

左上角的图是Isometric（等轴测图），右上为Front view（正测图），左下为Top view（俯视图），右下为Side view（侧视图）。

优点：1.能保存物体的形状。
2.可用于测量（例如建造计划、手册等）。

缺点：1.无法看到物体真实样子，因为很多面没有展现在图中（因此我们经常加一个Isometric（等轴测图）去解决这个问题）。

5.2.4.3 Axonometric projections（轴测投影）

运行投影平面相对于物体进行移动。
又按照投影立方体的一个角的角度数量进行分类，分为只有一个角相同（三个角的数量都不同）的是Trimetric（等轴斜测），两个角相同的是Dimetric（等角斜测），三个角都相同的是Isometric（等轴测）。



优点：1.可以知道线条的缩放情况。
2.可以保存线条。
3.大部分情况下可以看到物体的三个主要面（适用于与立方体类似的物体）。
4.用于CAD软件。

缺点：1.无法保存角度（例如非平行与投影平面的圆会被投影成椭圆）。
2.由于视觉上的一些变形，导致平行线再投影中可能会被拉伸或压缩从而导致其看起来会发散或收敛，这种情况在Dimetric（等角斜测）和Trimetric（等轴斜测）中尤为明显。（如上图前两个正方体有点变形）
3.由于它是平行投影的一种，因此他不符合近大远小，远处的物体和近处的物体一样大，从而显得物体不真实。

5.2.4.4 Oblique projection（斜投影）

投影线与投影平面之间呈任意关系。

优点：1.可以通过调整角度去强调任意的面。
2.在建筑上常使用Plan oblique（平面斜投影）和Elevation oblique（立面斜投影）。
3.在保存了平行于投影面的面的角的同时我们还可以看到周围的面。如图所示。

缺点：1.无法在现实世界中用普通的相机去创造斜投影（可以使用特殊的相知比如用褶叠暗箱照像机或者专门的建筑摄影镜头去实现斜投影）。

5.3 Co-ordinate parameters for 3D viewing

Viewing（视图）由三个方面组成，这些是在管线中实现的（见4.1）：
1.定位摄影机，也就是设置model-view matrix。
2.选择镜头，也就是设置projection matrix。
3.裁剪，也就是设置view volume（视锥体）。

虚拟世界中我们先选择一个点作为观察点，这个点可以被称为viewing point、view point、viewing position、eye position、camera position）。
接着我们确定一个观察方向，这个观察方向的负向量将是观察平面的法向量。从而我们确定了观察平面。

从一个参考点到观察点的方向可以被视为观察方向（向量），而这个参考点被称为观察目标点。

观察方向确定为$z_{view}$的方向，而$x_{view}$和$y_{view}$是任意的，这三个方向相互垂直。例如unity里的z轴被定义为前进方向，与人眼的观察传播方向相同，这一点与OpenGL相反。

一旦观察平面法向量$N$确立，就可以设置观察上升向量$V$也可以确立从而确定$x_{view}$轴。
由于$N$定义了$Z_{view}$，所以$V$一定垂直于$N$，即平行于$x_{view}-y_{view}$平面。
但是精确定义$V$通常很困难，因此观察例程通常会调整用户定义的$V$值。例如，将其投影到与$N$垂直的平面上）。
只要$V$不与$N$平行，任何方向都可以用作$V$。
如下图所示，将$V$投影到与观察平面评选的的平面来确定$X_{view}$，这样即使输入的$V$不完全垂直于$N$，也可以确保$X_{view}$的正确性。

5.4 Orthogonal projection（正交投影）

正交投影（正投影）是一种将物体转换到一个视图平面上的变换，这个变换沿着与视图平面法向量平行的线进行。

工程和建筑的图经常使用正交投影因为它可以正确地描述长度和角度，图纸上这些可以被测量出来。

这张图你也可以看出$z_{view}$是和观察方向相同。

这一步体现出了projection transform后的结果在normalization transform的作用下化为了单位cube的结果，从而方便后续的操作。

5.5 Perspective projection / Frustum projection（透视投影/视锥投影）

通过添加近处和远处的与观察平面平行的裁剪平面，可以将无限透视视图体的部分部分截取从而形成棱台或者视锥体。
近裁剪平面和远裁剪平面用来围住需要显示的物体。在一些系统中这些裁剪平面是可以选择的。
近裁剪平面可以用来移除靠近观察平面的大型物体，因为这些物体在裁剪窗口中可能会被投影成难以识别的形状。同样，远裁剪平面可以剔除可能被投影成小斑点的物体。通过这样的形式，我们可以自由选择我们想要显示的物体。

一些系统限制了观察平面相对于近裁剪平面和远裁剪平面的位置，而其他系统则允许观察平面可以被放置在任何位置，除了观察原点（视点、观察位置、眼睛位置或摄像机位置）的位置。
放置在任意位置中，如果观察平面放在了投影参考点的后方，那么物体在观察平面上会被倒置。此时如果物体被投影到远处，物体会简单地放大。
当投影参考点离观察平面非常远时，透视投影逐渐接近平行投影。

5.6 OpenGL functions

1.gluLookAt(eye_position, look_at, look_up)用于定义观察坐标系，从而将场景中的物体变换到这个坐标系下进行观察。

2.glOrtho(GLfloat left, GLfloat right, GLfloat bottom, GLfloat top, GLfloat near, GLfloat far)用于定义正交投影矩阵，这些参数确定了正交投影矩阵的六个面的位置。

3.glFrustum(GLfloat left, GLfloat right, GLfloat bottom, GLfloat top, GLfloat near, GLfloat far)用于定义透视投影矩阵，这些参数确定了视锥体的六个面的位置。
它既可以创建对称的透视投影矩阵也可以创建斜切的透视投影矩阵。

4.gluPerspective(GLfloat fov, GLfloat aspect, GLfloat near, GLfloat far)用于定义透视投影矩阵的函数。它通过指定视场角（fov）、宽高比（aspect）、近裁剪面距离（near）和远裁剪面距离（far），来创建一个透视投影矩阵。它通常用于创建对称的透视投影矩阵。