文章目录
- 6. Parametic Curves and Surfaces(参数曲线和参数平面)
- 6.1 Why we need parametric curves and surfaces?
- 6.2 Parametric curves(参数曲线)
- 6.3 Splines, interpolation and design curves
- 6.4 Local control
- 6.5 Revolved, extruded and swept surfaces
- 6.6 Tensor product surfaces(张量积曲面)
- 6.7 Bézier and B-Splines surfaces(贝塞尔曲面和B-样条曲面)
- 6.8 Trimming and control(修剪和控制)
- 6.9 Improving resolution(提高分辨率)
- 7. 3D Modelling
- 8.Hierarchical Modelling(层次建模)
6. Parametic Curves and Surfaces(参数曲线和参数平面)
其实这可能不是我们第一次遇到Parametic curves,我们曾经在JavaFX中使用过Cubic curve,那个函数可以指定起始点、终点和控制点从而画出我们想要的曲线路径。
JavaFX的相关实践可以看这里:JavaFX教程
6.1 Why we need parametric curves and surfaces?
6.1.1 Parametric curves
1.能对自然曲线物体有更好的3D渲染。
2.折线是由一系列的直线组成的,可能无法准确地描述复杂曲线地形状,可能结果不够真实、平滑,而参数曲线更灵活且准确。
6.1.2 Parametric surfaces
1.参数化曲面使用两个独立的参数来表示曲面。
2.可以相对容易地表示自交或不可定向的曲面。
3.使用隐式函数来表示这些曲面很多是不可能的。
4.即使可以使用隐式函数,其tessellated representation(镶嵌表示)通常也是不正确的。
6.2 Parametric curves(参数曲线)
2D参数曲线:(x(t), y(t))。
参数曲线通常使用一个参数(通常为t)来描述曲线上的点的位置,它沿着曲线的轨迹变化,从而确定曲线上的点的位置。
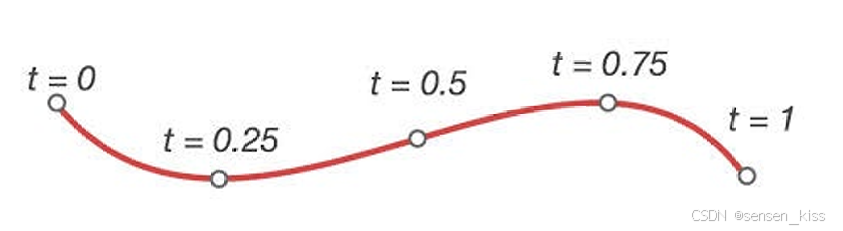
6.2.1 Straight Line(直线)
隐式表达:
y
=
a
0
+
a
1
x
y = a_0 + a_1x
y=a0+a1x
参数表达(显式表达):
x
=
x
1
+
t
(
x
2
–
x
1
)
(
0
≤
t
≤
1
)
x = x_1 + t(x_2 – x_1) (0 ≤ t ≤ 1)
x=x1+t(x2–x1)(0≤t≤1)
y
=
y
1
+
t
(
y
2
–
y
1
)
y = y_1 + t(y_2 – y_1)
y=y1+t(y2–y1)
当
t
=
0
,
x
=
x
1
,
y
=
y
1
t = 0, x = x_1, y = y_1
t=0,x=x1,y=y1
当
t
=
1
,
x
=
x
2
,
y
=
y
2
t = 1, x = x_2, y = y_2
t=1,x=x2,y=y2

6.2.2 Circle(圆形)
隐式表达:
x
2
+
y
2
=
r
2
x^2 + y^2 = r^2
x2+y2=r2
参数表达:
x
=
r
c
o
s
(
360
t
)
,
y
=
r
s
i
n
(
360
t
)
,
(
0
≤
t
≤
1
)
x = r cos(360t), y = r sin(360t), (0 ≤ t ≤ 1)
x=rcos(360t),y=rsin(360t),(0≤t≤1)

6.2.3 Cubic curve(三次曲线)
x
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
(
0
≤
t
≤
1
)
x(t) = a_0 + a_1t + a_2t^2 + a_3t^3 (0 ≤ t ≤ 1)
x(t)=a0+a1t+a2t2+a3t3(0≤t≤1)
y
(
t
)
=
b
0
+
b
1
t
+
b
2
t
2
+
b
3
t
3
(
0
≤
t
≤
1
)
y(t) = b_0 + b_1t + b_2t^2 + b_3t^3 (0 ≤ t ≤ 1)
y(t)=b0+b1t+b2t2+b3t3(0≤t≤1)
对于不同的三次曲线我们这里的
a
i
,
b
i
a_i,b_i
ai,bi取不同的值。

6.3 Splines, interpolation and design curves
6.3.1 Interpolation(插值)
任意曲线我们可以有表达式:
x
(
t
)
=
a
0
+
a
1
t
+
a
2
t
2
+
a
3
t
3
,
+
…
+
a
n
t
n
x(t) = a_0 + a_1t + a_2t^2 + a_3t^3, + … + a_nt^n
x(t)=a0+a1t+a2t2+a3t3,+…+antn,显然当我们的表达式如果是高次多项式的时候,所需的计算量就会很大。因此我们可以使用插值技术从而用低次多项式曲线取逼近高次多项式曲线,从而减少计算量。
为了找到更精确的
a
i
a_i
ai,在有k个点的情况下我们需要n = k - 1个点去插值。
ex:对于直线来说,它的控制点k = 2,因此 n = k - 1 = 1.
对于parabola(抛物线)来说,它的控制点k = 3,因此 n = k - 1 = 2.
6.3.1.1 为什么我们不使用高次多项式进行插值?
如果我们使用高次多项式进行插值,在控制点的数量k很多时,高次多项式会在曲线的两端产生剧烈的震荡。
如下图所示,红色为想要产生的曲线,而黑色是插值产生的曲线。

使用低次多项式还可以简化计算,与高次多项式相比更高效。
因此我们在面对有大量控制点的曲线时,我们将这些点分为多个小的集合,比如每个集合包含4个点,然后对每个小集合中的4个点用低次多项式进行插值,从而使用三次多项式,画出这些曲线,最后将这些曲线平滑的曲线连接起来。这就是分段插值法(Piecewise Interpolation)。
由于低次高项式可以简化计算、减少震荡、平滑连接,因此我们使用低次多项式进行插值。
分段插值法是Spline curve(样条曲线)的基础。
6.3.2 Splines(样条)
样条插值通过将整个曲线或曲面分解为多个小的曲线段或曲面片来进行插值,每个小段用低次多项式(通常是三次多项式)组成,最后将这些小段平滑地连接在一起。
6.3.2.1 连续性的各种要求
在曲线或曲面设计中,通常需要满足不同类型的连续性要求:
1.曲线的连续性(没有断裂)。
2.切线的连续性(没有尖锐的转折)。
3.曲率的连续性(非必需,但可以避免一些光照方面的伪影)。
6.3.2.2 Interpolation and design curves(插值曲线和设计曲线)
插值曲线:
1.插值曲线定义了曲线必须通过的确切位置(点),例如在关键帧动画中,物体必须在特定的时间点处位于特定的位置。
2.插值曲线的形状取决于提供的数据点。
设计曲线:
1.设计曲线定义了曲线的一般行为,例如曲线应该是什么样子,并且通常需要调整曲线的形状。这种方法通常由设计师使用。
2.设计曲线的形状取决于控制点,这些点并不位于曲线上,但可以通过移动这些点来调整曲线的形状。
因此由上面的定义可以看出,我们JavaFX的CubicCurve是设计曲线,而非插值曲线。

设计曲线是由多个分离的部分组成在一起,这些部分每个都可以独立地进行调整,然后再将它们连接在一起形成完整地曲线。
这意味着对于一条曲线来说,我们修改它的其中一部分,不会影响其他部分。这是局部调整的关键——不影响已经完成的部分,而只我们想要影响的曲线的一小部分。
6.4 Local control
缺少局部控制的曲线:
1.Natural splines(自然样条)
自然样条在曲线的两端,通常是第一个和最后一个数据点处,会施加额外的条件,从而确保曲线在两端的行为更加自然平滑。也因此它无法实现局部控制。
2.Bezier curves(if continuity enforced)(对连续性有严格要求的贝塞尔曲线)
有局部控制的曲线:
1.B-Splines(B-样条)
2.NURBS(Non-Uniform Rational B-Splines)(非均匀有理B-样条)
一个具有局部控制的三次曲线:
通常只会被4个控制点影响,因此最直接影响它形状调整的就是这4个控制点。
比如三次贝塞尔曲线,而JavaFX中使用的CubicCurve就是三次贝塞尔曲线。
在设计曲线中除了控制移动点外,有的曲线还提供了额外的参数,以保证控制点不变的情况下,对曲线进行一定程度的调整,这些额外的参数包括tension(张力)和bias(偏移)。
这些控制方法除了应用于设计曲线还可以应用于插值曲线。
下图展示了参数tension(张力)和bias(偏移),tension(张力)越高,两个点之间就越“紧”,或者说越像直线。而bias(偏移)控制其向哪边偏移。

6.5 Revolved, extruded and swept surfaces
讲完参数曲线,现在介绍参数平面。
6.5.1 Revolved surface(旋转曲面)
一个二维曲线绕着一个轴旋转得到的三维曲面。这个过程中的参数是旋转角度。

6.5.2 Extruded surface(挤压曲面)
通过沿着二维曲线的法线方向移动该曲线来创建一个三维曲面。这个过程中的参数是移动的直线深度。

6.5.3 Swept surface(扫描曲面)
一个二维曲线沿着一个三维路径进行移动,从而创建一个三维曲面。这个过程中参数是路径的定义。

6.6 Tensor product surfaces(张量积曲面)
最重要的参数化平面是Tensor product surfaces(张量积曲面),它是使用最广泛的参数化平面。
张量积曲面是由两个参数曲线组合而成的,这两个曲线在垂直方向上运行。
比如前面的扫描曲面,可以视为是一个张量积曲面,曲线屏幕依赖的两个参数分别是u和v。
6.7 Bézier and B-Splines surfaces(贝塞尔曲面和B-样条曲面)
我们前面介绍了插值曲线和设计曲线,同理曲面有插值曲面和设计曲面。
它使用一个控制网格,通常是一个控制点的矩形数组,来进行局部控制,由于曲线是分成了更小的曲线,所以曲面也被分成了更小的曲面patches(片段)。在这种情况下我们的局部控制更加重要。
在具有局部控制的Cubic curve(三次曲线)中,一个曲线段通常受到4个点的控制,因此在一个Cubic surface(立方曲面)中,一个曲面patch(片段)受到16个点的控制,形成了一个4x4的网络。

当我们在曲面patch(片段)的连接时(多个曲面片段被组合在一起形成一个更大的曲面时),曲面片段的连接并不总是直接的。我们需要在曲面片段连接时考虑如何确保曲面的整体连接性。

6.8 Trimming and control(修剪和控制)
6.8.1 Trimming(修建)
当我们部分的曲面不需要展示出来的时候,我们可以定义trim line(修剪线),在修剪一侧的曲面部分将被移除,另一侧将被保留。从而减少渲染的花费。
注意Trimming操作是在建模阶段的,而Clipping操作是在变换阶段的,但两者都是为了提高渲染的效率。
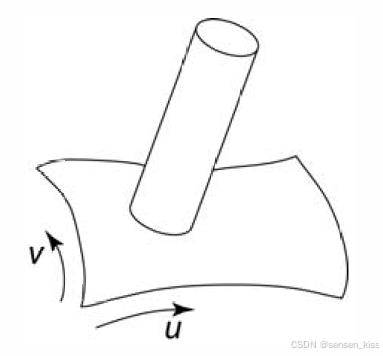
6.8.2 Control(控制)
控制曲面的方法与控制曲线的方法类似,包括移动控制网格中的点,这样可以直接调整曲面的形状。此外,对于某些类型的曲面,还可以使用张力和其他参数来调整曲面的特性,而无需移动控制网格中的点。
6.9 Improving resolution(提高分辨率)
为了获取更精确的细节,可以增加曲面的片段数量。
有时候我们可以根据需要,自适应调整增加片段数量的方法,比如只在需要展示细节的地方增加片段数量。这样可以节省计算量。
然而这种自适应增加可能会导致cracks(裂缝)的产生,因此在增加片段的时候需要小心。而这种cracks(裂缝)的产生,是因为曲面的连接不是直接的或者说不是无缝的。

7. 3D Modelling
7.1 Wireframe modelling(线框建模)
是一种最古老且最简单的方法。
它用简单的点和线条来表示物体的形状和结构,用线框的形式来表示物体的外部和内部结构,而不考虑颜色、纹理或光照等表现形式。
空间曲线可以使用参数方程或者隐式方程来表示。
缺点:1.模型有模糊性以及难以验证模型。(没有线条之间的关系,因此难以确定物体的真实形状)
如图所示。
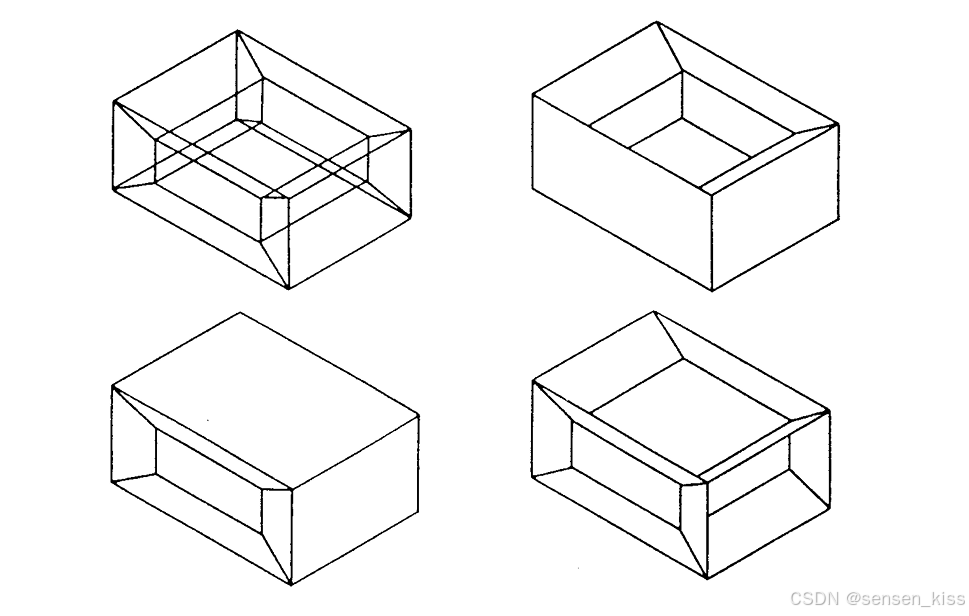
2.无法提供与曲面和体积相关的信息。
7.2 Surface modelling(曲面建模)
与线框建模相比,它生成的对象具有更完整、更清晰的表达。
因此它具有更多的应用,例如设计和车模型的表达。
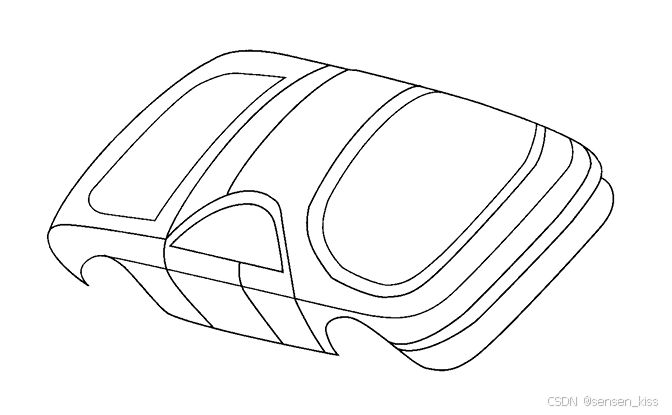
曲面是由点和曲线构成的,曲面可以是二维的,也可以是三维的,通过曲线的闭合环形成表面,最简单的形式是一个平面。
这种表示方法在建模对象时非常重要,能够满足大多数情况下对3D模型的要求。
建模软件通常提供一系列有用的曲面创建功能,其中一些类似于曲线的创建方法,但其几何特征是不同的。
曲面模型只描述了物体的外表面几何特征,而没有包含实体模型所具有的体积信息。
如图所示,它看起来像是一个实体,但实际上是空心的。
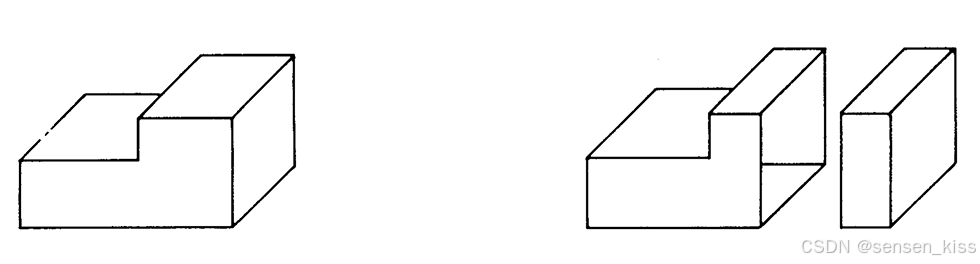
7.3 Solid modelling(实体建模)
实体建模对固体物体的几何特性(如点、曲线、曲面、体积、形状的中心)和物理特性(如质量、重心和惯性)进行了全面的表示。
建模方式有:primitive instancing(基本实例化)、cell decomposition(单元分解)、constructive solid geometry(CSG, 构造性实体几何)、 boundary representation(B-Rep, 边界表示)。
其中CSG和B-Rep是最流行的实体建模方案。
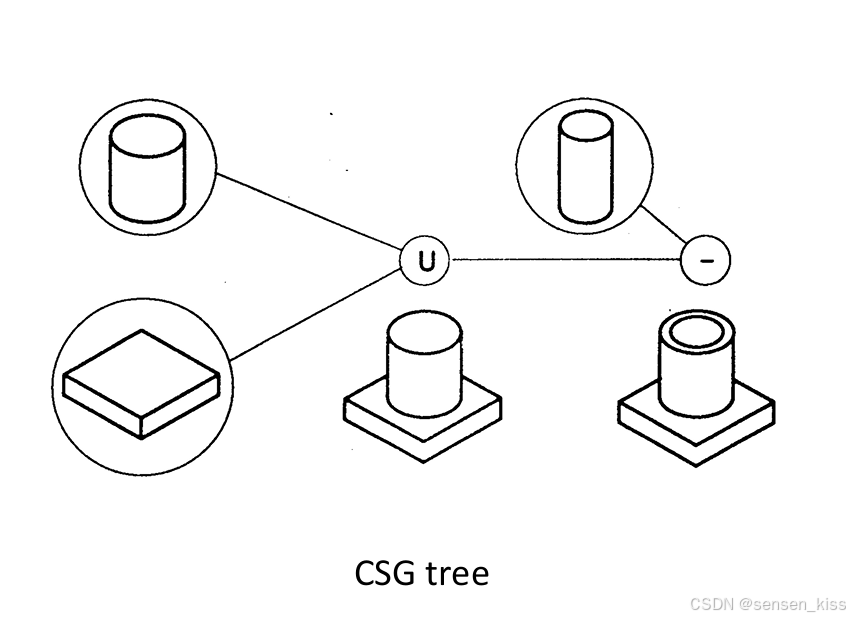
7.4 Constructive solid geometry(CSG, 构造性实体几何)
CSG模型是一种有序的二叉树,其中非终端节点代表操作符,而终端节点则是原始对象或变换操作。这些操作符可以是刚体运动或常规的布尔运算。原始叶子节点是建模是建模空间中的基本实体,而变换叶子节点则定义了rigid(刚体)运动的参数。
如图所示。
布尔运算符包括Boolean Union(布尔并集)、Boolean Difference(布尔差集)和Boolean Intersection(布尔交集),布尔运算符的结果不仅取决于不同的实体还取决于实体的位置和方向,因此不同的位置和方向可能会有不同的结果。
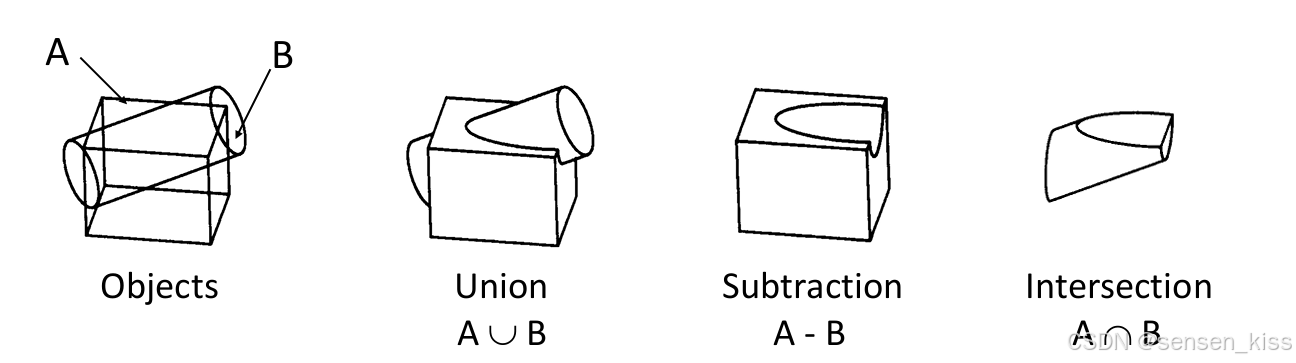
每个实体通常都有自己的局部坐标系,它们相对于全局的世界坐标系进行定义。在进行布尔运算之前,可能需要对实体进行平移和/或旋转,以便获得所需的相对位置和方向关系。
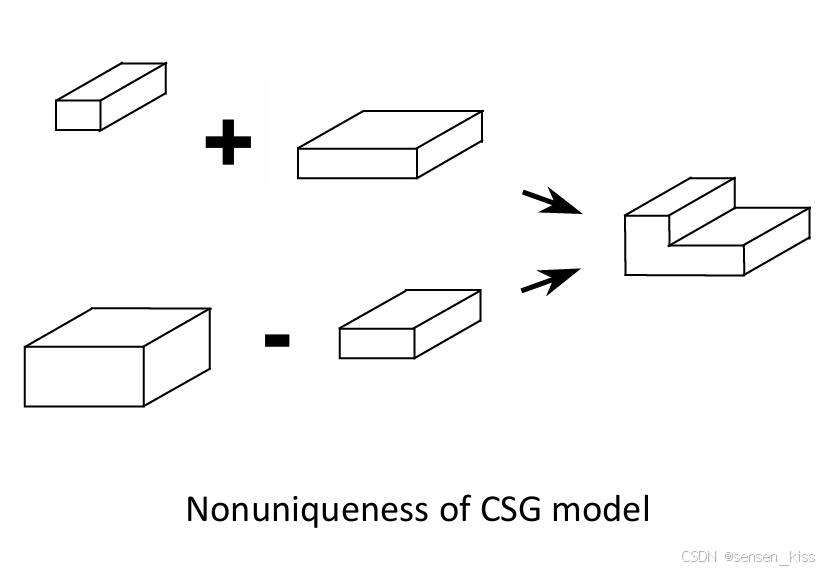
如果一个对象可以用唯一的数据集表示,那么这种表示被称为唯一的。对于某些应用(比如几何推理),表示方案理想情况下应该是既明确又唯一的。这意味着表示对象的数据应该清晰明确,同时也应该是唯一的,不会存在歧义或多重解释。实体的表示通常是明确的,但很少能够做到唯一,而且让CSG(Constructive Solid Geometry)表示唯一是不可行的。
如下图所示。
7.5 Boundary representation(B-Rep,边界表示)
B-Rep模型通过将实体的边界分割成有限数量的有界子集来表示实体(关于几何和拓扑结构)。
The geometry(几何)涉及到边界实体的形状和大小,包括点、曲线和曲面,而the topology(拓扑)则涉及到边界实体之间的连接性,包括顶点、边和面(对应于点、曲线和曲面)。
B-Rep基本上是一种topologically explicit(拓扑显式)表示,其中几何和拓扑信息都存储在数据结构中。
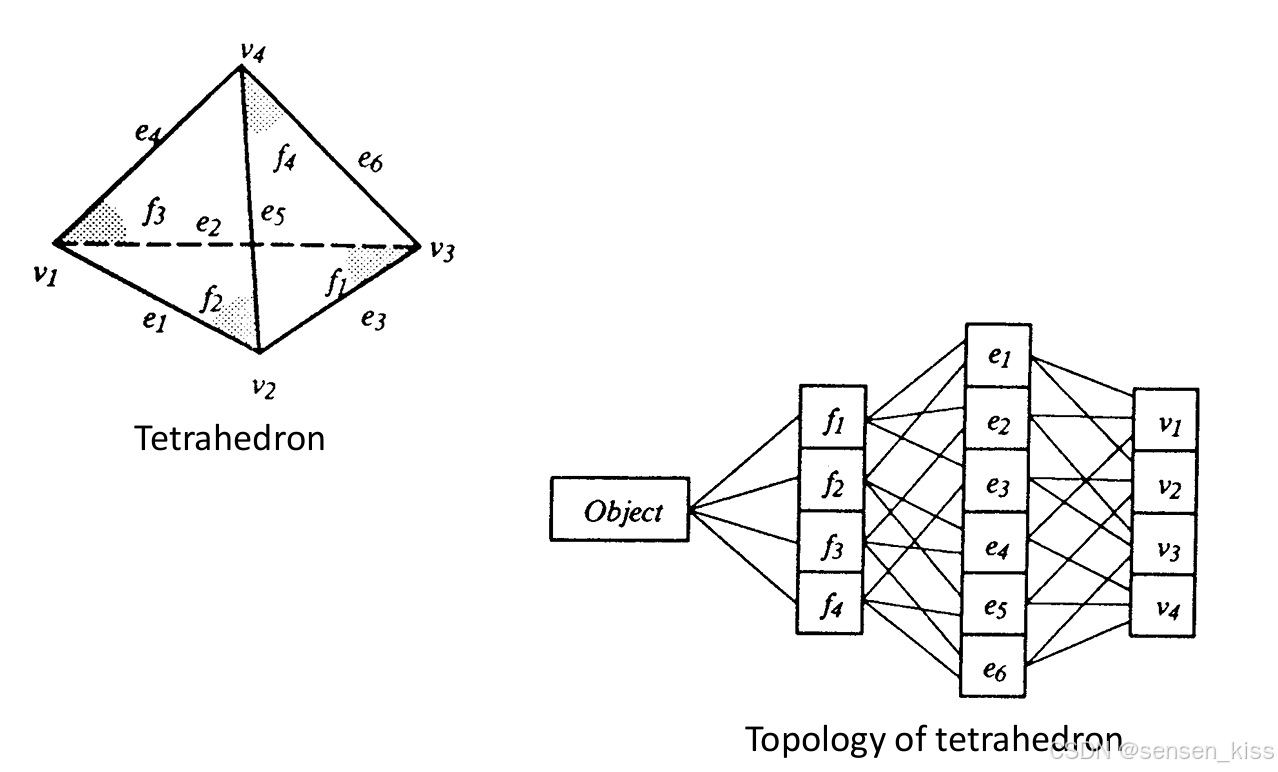
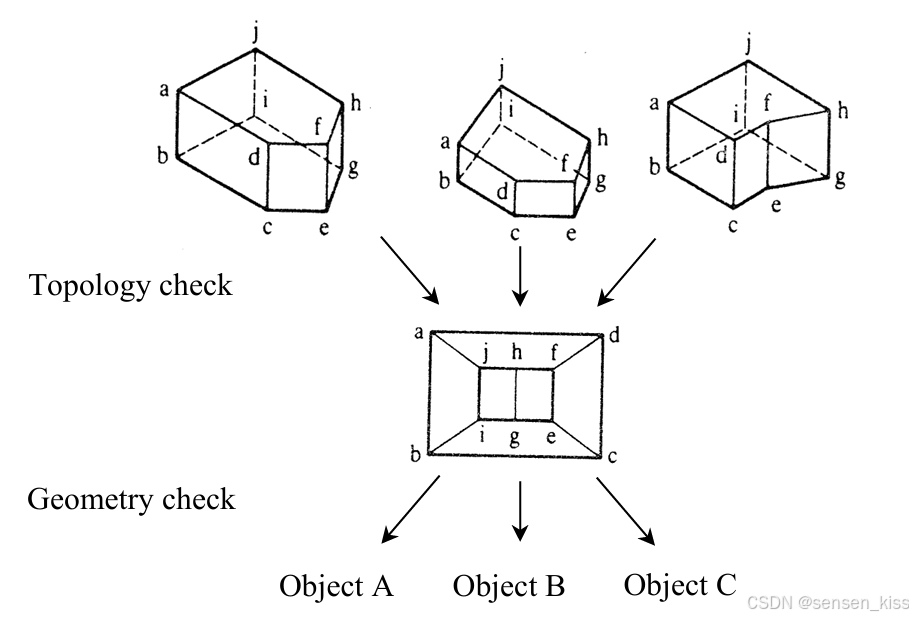
相同的拓扑结构可能代表不同的几何形状和大小,因此需要考虑同时考虑拓扑和几何数据,才能完全和唯一地定义一个对象。
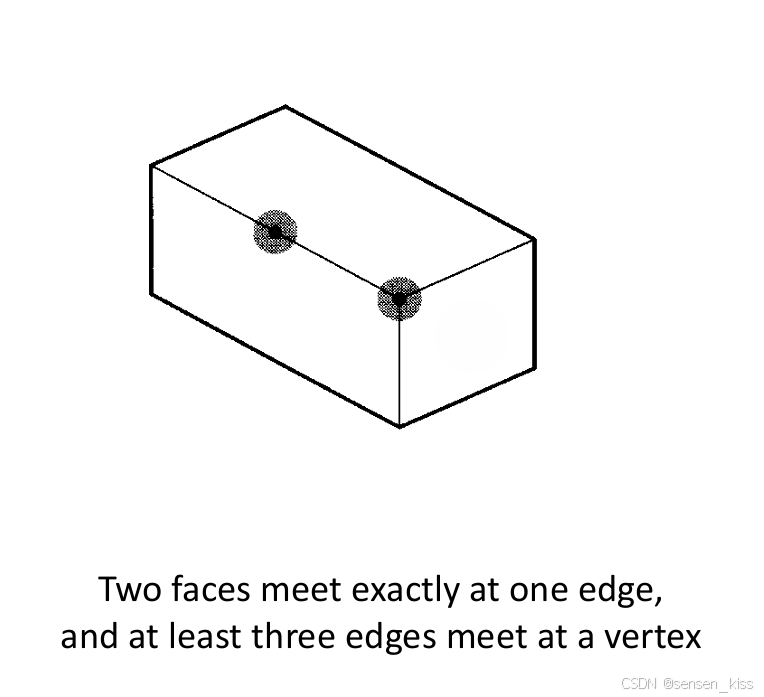
B-Rep有两种类型:manifold(流形)和nonmanifold(非流形)。
在流形模型中,一条边连接恰好两个面,而一个顶点连接至少三条边。因此更符合现实世界物体地特征。
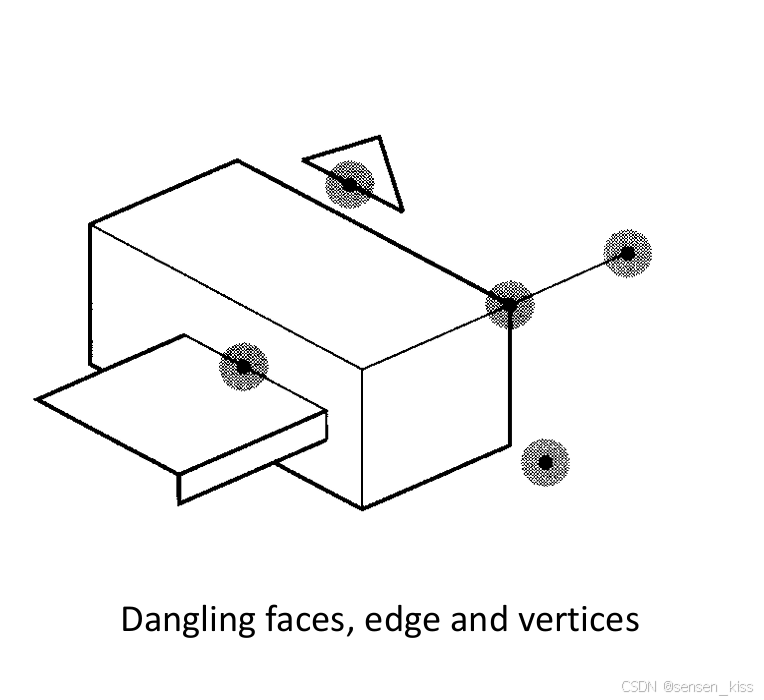
非流形模型可能会包含悬挂的面、边和顶点,因此代表了一个非现实的、非物理的对象。
7.5.1 Euler’s law for manifold B-Rep
为了确保一个固体(即流形模型)的拓扑有效性,一个流形模型一定满足以下欧拉公式:
V
−
E
+
F
−
R
+
2
H
−
2
S
=
0
V-E+F-R+2H-2S=0
V−E+F−R+2H−2S=0
其中,V表示vertices顶点的数量,E表示edges边的数量,F表示faces面的数量,R表示rings环的数量(inner loops on faces面内环的数量,或者可以理解成连接的地方),H表示passages/holes孔的数量(亏格),S表示shells壳体的数量(disjoint bodies不相交的实体数量)。
欧拉公式的一个简化形式(即没有环和洞但是有一个壳体):
V
−
E
+
F
−
2
=
0
V-E+F-2=0
V−E+F−2=0,这个简化形式适用于简单的多面体,即没有内环和孔的对象。例如:三棱锥就是流形模型,因为
4
−
6
+
4
−
2
=
0
4-6+4-2=0
4−6+4−2=0
我们这里看一个比较难的例子:
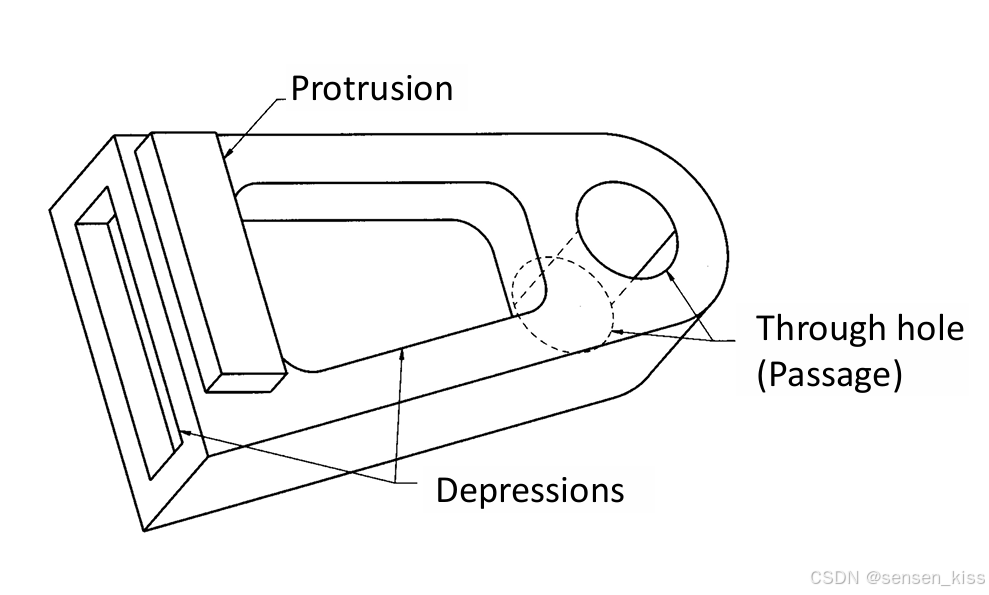
我们将这个物体看作是一个稍微变形的长方体多了一个passage(孔),以及一个protrusion(突出物),两个depression(凹陷),然后我们分开计算这些部分,因此我们的主体
V
=
8
,
E
=
12
,
F
=
6
,
S
=
1
V = 8, E = 12, F = 6, S = 1
V=8,E=12,F=6,S=1,前面与正常长方体一致,其中的hole是一个圆柱体,圆柱体我们将其理解成上面两个点,下面两个点,然后上下两个面,周围两个完全的面组成,因此一个圆柱体由4个顶点,6条边,4个面组成,而在此处,由于是passage,所以上下两个面没有。所以是4个顶点,6条边,2个面,和这个大的长方体有两个地方连接,所以有两个环。其余的地方因为和大的长方体连接在一起,所以少了一个面,但是多了一个环。最后的结果
44
−
66
+
27
−
5
+
2
×
1
−
2
×
1
=
0
44-66+27-5+2×1-2×1=0
44−66+27−5+2×1−2×1=0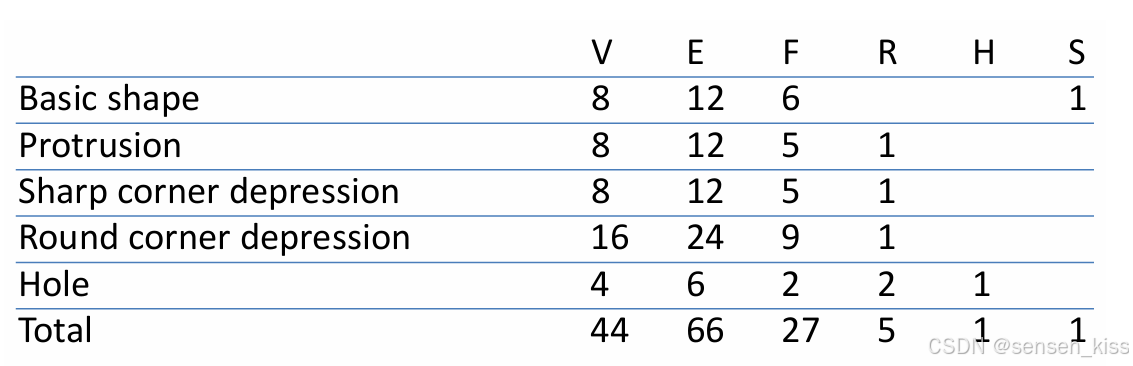
7.5.2 Implement of B-Rep
在计算机上,B-Rep模型可以通过在数据结构中将拓扑结构表示为指针,将几何信息表示为数值信息,然后利用面向对象编程(OOP)技术(例如C++)进行提取和操作来方便地在计算机上实现。
同时最新的B-Rep模型还提供了标记属性的功能,比如颜色、公差和表面光洁度等,这对于诸如计算机辅助设计和制造(CAD/CAM)等应用非常有用。
如图,图中的一条边以两个顶点结束,然后每个顶点还有其他边与之相连。
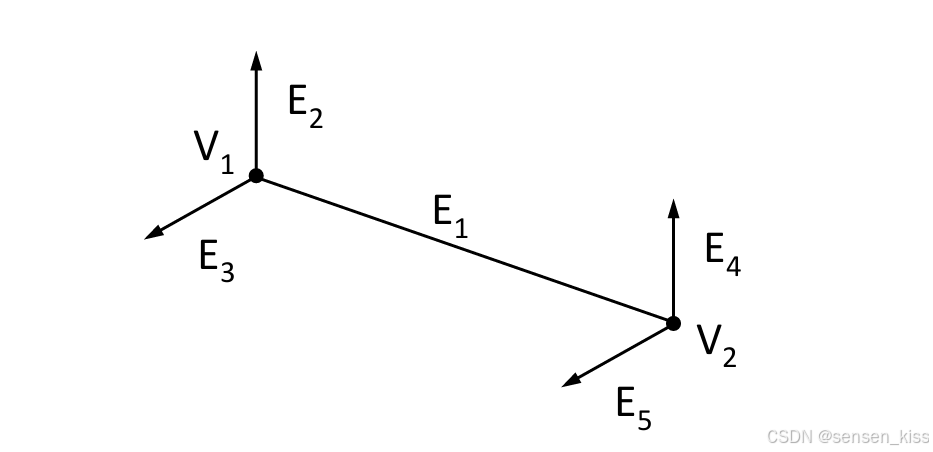
7.5.2.1 Baugmart’s winged edge data structure
Baugmart’s winged edge data structure是一种表示图形其中边具有指向其端点顶点和相邻边的指针。顶点具有指向它们的坐标的指针。
如图所示。
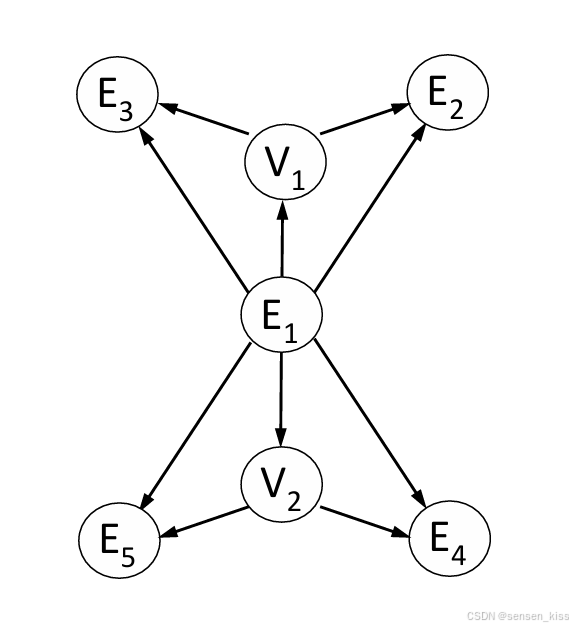
7.5.2.2 Euler-operators
许多B-Rep建模系统具有称为欧拉操作符的过程。 这些操作符以一种方式修改面-边-顶点指针结构,以确保欧拉公式始终成立。
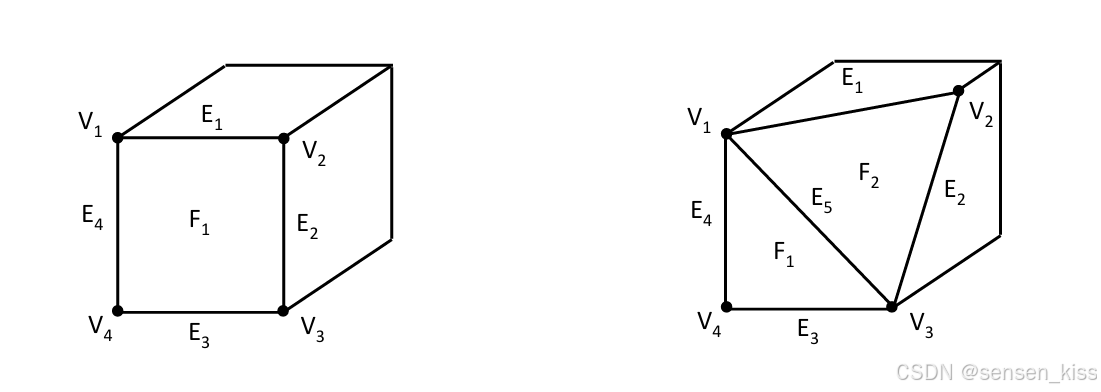
如图所示,我们使用了函数 make_edge_and_face(f1, v1, v3),将左边的长方体沿着对角线分割成两个面,从而创建了一个新的对象。注意原来的长方体的v1,v2,v3和v4全部都在一个平面,但是新的对象的v2可以自由的沿着右上角的边进行移动。
7.5.3 B-Rep Geometric Modellers(B-Rep实体建模器)
Romulus建模内核也被称为Romulus(B-Rep实体建模器),是第一款商业实体建模内核并被设计用于直接集成到CAD软件中的。
ACIS(Alan,Charles and Ian’sSystem)是由Spatial Corporation发展而来,Spatial Corporation的前身是Spatial Technology,它是Dassault Systems的一部分。ACIS被许多开发人员在计算机辅助设计(CAD)、计算机辅助制造(CAM)、计算机辅助工程(CAE)、建筑、工程和施工(AEC)、坐标测量机(CMM)、3D动画和造船等行业使用。
8.Hierarchical Modelling(层次建模)
8.1 Local and world co-ordinate frames of reference(本地坐标系和世界坐标系)
其实我们的现实世界没有(0,0,0),因此物体的位置通常是相当于其他物体或参考店来定义的。通过移动(0,0,0),我们就移动了所有相对于该原点定义的点。
这些术语通常可以互换使用:
Local basis (本地基准)
Local transformation (本地变换)
Local / model frame of reference (本地/模型参考系)
这些术语都指代我们所用的(0,0,0)在整个世界中的位置。它们还包括了当前本地坐标系的概念,即关于 x、y、z 轴的方向。通过旋转坐标系的本地框架,我们可以旋转它所描述的世界。
对于一个物体场景,会定义一个世界参考系。每个物体都有一个本地参考系,而这个本地参考系是相对于世界参考系来定义的。
因此我们在一些场景的时候我们需要考虑物体的相对运动。
8.2 Linear modelling(线性建模)
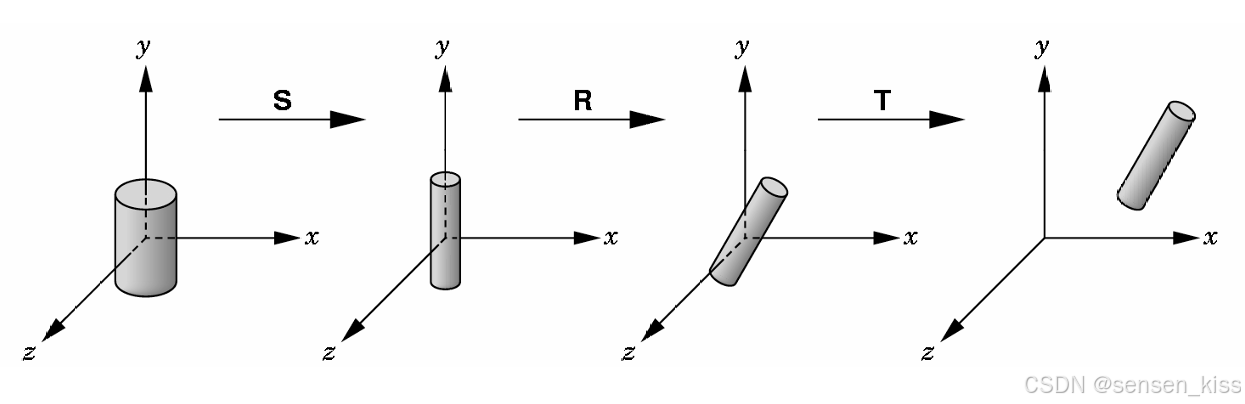
线性建模是指使用线性方程或线性函数来描述变量之间的关系。在线性建模中,变量之间的关系被假设为线性的,这意味着当一个变量发生改变时,其他变量的变化是按照一个固定的比例关系来发生的。从一个符号或原型开始,然后对这Symbol(符号/原型)进行实例化时变换,过程公式为M=TRS。这个公式代表了对符号进行平移(T)、旋转(R)和缩放(S)的组合变换。
在应用时先进行缩放变化,然后是旋转变换,最后是平移变换。这种顺序是从右到左的,与矩阵乘法的规则是一致的。虽然公式是以TRS的顺序呈现,但实际应用变换时,需要按照SRT的顺序来进行。这种顺序确保了正确的变换顺序和结构。
在OpenGL中,我们可以设置适当的变换,将模型坐标系转换到世界坐标系。
在执行代码之前,将这些便会按应用到MODELVIEW矩阵中。
glMatrixMode(GL_MODELVIEW); // M = T⋅R⋅S
glLoadIdentity();
glTranslatef();
glRotatef();
glScalef();
glutSolidCylinder()// or other symbol
这里的Symbols就是Primitives(基础图元),可以是Cone(圆锥体), Sphere(球体), GeoSphere(地球球体), Teapot(茶壶), Box(盒子), Tube(管子), Cylinder(圆柱体), Torus(圆环)等。
在创建和操作图形对象时,copy(复制)和instance(实例)是两种不同的复制方式。
Copy(复制)创建一个完全独立的克隆对象,对克隆对象的修改不会影响原始对象。
Instance(实例)创建一个完全可互换的克隆对象,对实例化对象的修改与修改原始对象是相同的,因此对实例化对象的修改会影响到所有的实例化对象,就好像修改了原始对象一样。
用Array描述一系列克隆对象的排列方式。其中有两种不同的数组方式:Linear array(线性数组)和Radial array(径向数组)。
Linear array(线性数组)指的是沿着一个轴线方向排列的一系列克隆对象。需要选择对象,定义一个轴线,指定克隆对象之间的距离以及克隆的数量。这样就可以沿着指定的轴线方向创建一系列等距离排列的克隆对象。
Radial array(径向数组)指的是沿着一个轴线以及围绕一个中心点的一系列克隆对象。需要选择对象,定义一个轴线,指定半径以及克隆的数量。这样就可以围绕指定的轴线和中心点创建一系列等距离排列的克隆对象。
图形学中将模型存储在表中,通过为每个符号分配一个编号,并存储实例转换的参数来实现。这种方法包含了平面信息,但没有关于实际结构的信息。如图所示。
这难以解决一些与复杂结构以及如何处理子结构的操作相关的问题。如图所示。
8.3 Scene hierarchy(场景层次结构)
Scene hierarchy(场景层次结构)是一种组织和管理场景中的各个元素的结构化方式。这种结构通常是一种树形结构,用于描述场景中的各种对象之间的层次关系和组织结构。例子如图所示。
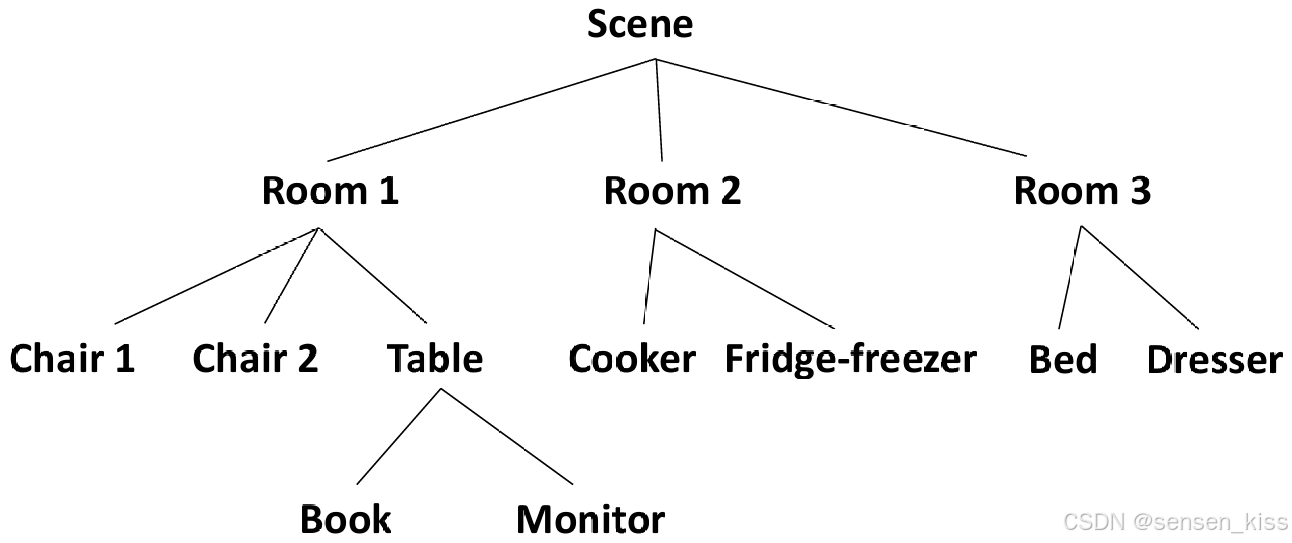
我们可以在一个场景中,将一些物体以某种方式组合在一起。例如可移动的人物模型可能包含若干个刚性组件以特定的方式连接在一起,,或者一些物体放在一个托盘上,而托盘正在被携带着移动,或者一些卫星和行星围绕太阳系中心运行,又或者一个酒店包含200个客房,每个客房里都有床、桌子、椅子等这样的情况,我们考虑物体相对于彼此的位置和方向时,描述物体的相对位置和方向会更容易一些。
8.4 Hierarchical models(层次化建模)
我们以前面的思想,可以将这种层次化的方法用到一些复杂对象的建模之中。
比如在汽车建模中我们可以将汽车理解成一个底盘和四个相同的车轮组成的,这是汽车的两个符号。其中车轮的旋转速度决定了汽车的移动速度。
下面的代码展示了一种做法,但这种做法并不推荐。
void main ( );
{
float s = ...;// speed
float d[3] = {...}; // direction
draw_right_front_wheel(s,d);
draw_left_front_wheel(s,d);
draw_right_rear_wheel(s,d);
draw_left_rear_wheel(s,d);
draw_chassis(s,d);
} // WE DO NOT WANT THIS!
8.4.1 Hierarchical tree(层次树)
我们更希望它更能展现层次化的特点,而非简单的绑定一些关系。我们可以使用hierarchical tree(层次树)去表示这种层次结构,就像前文表示一些复杂场景时候使用的方式一样。在这种情况下,各个物体被组织成一种由树状结构(倒置的树)表示的层次结构。在这种结构中:
每个可移动的部分都是树中的一个单独节点。
位于顶部的节点是根节点。
每个节点(除了根节点)只有一个直接位于其上方的父节点。
一个节点下面可以有多个子节点。
具有相同父节点的节点被称为兄弟节点。
没有子节点的位于树的底部的节点被称为叶节点。
因此我们回到前面的例子中,我们使用Direct Acyclic Graph(DAG,有项无环图)来储存每个车轮的位置信息。如图所示。
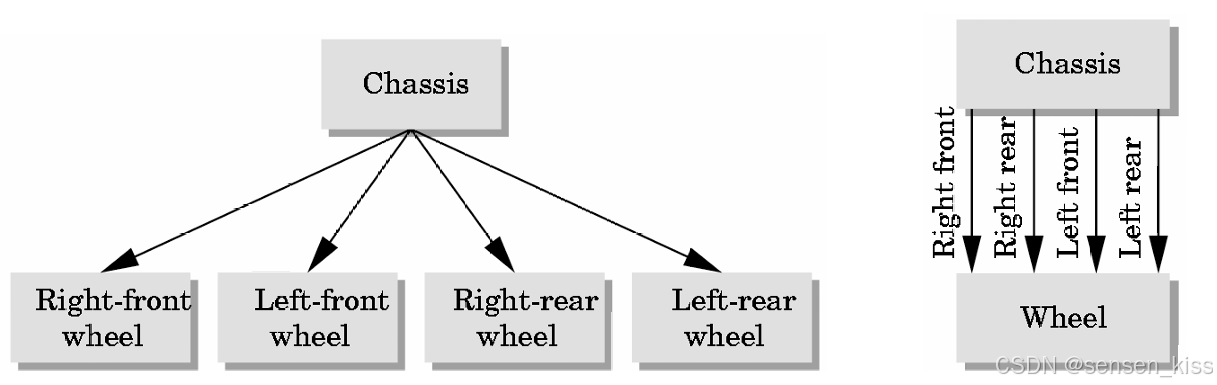
树和DAG常用于表示复杂对象之间的关系,特别是在描述动画中的关联和依赖关系时。
8.4.2 Articulated model(关节模型)
关节模型是一种层次化模型,由刚性部件和连接关节组成。在这种模型中,移动部件可以被组织成一种树状数据结构,其中选择某个特定的部件作为“根”。对于关节模型(比如双足角色),通常会选择位于躯干中心附近的某个部件作为根。每个关节在模型中具有特定的allowable degrees of freedom(DOFs,可允许自由度),这些自由度定义了模型可能姿势的范围。
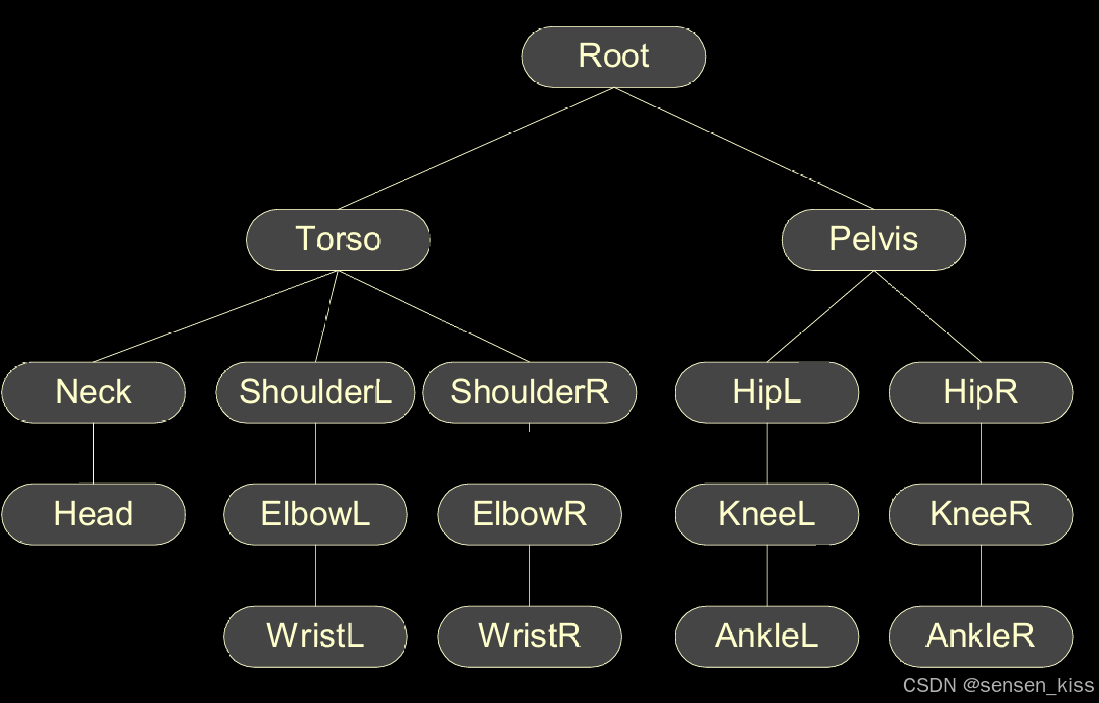
8.4.3 Hierarchical transformations(层次变换)
树中的每个节点代表一个对象,它具有描述其位置的矩阵和描述其几何形状的模型。当树中的节点进行矩阵变换时,它会将其子节点一起移动(换句话说,旋转一个角色的肩部关节会导致肘部、手腕和手指也一起移动)。因此,子节点会继承其父节点的变换。树中的每个节点都存储着一个局部矩阵,这是它相对于其父节点的变换。要计算一个节点的世界空间矩阵,我们需要将其局部矩阵与其父节点的世界矩阵连接起来,即 M w o r l d = M p a r e n t ⋅ M l o c a l M_{world} = M_{parent}·M_{local} Mworld=Mparent⋅Mlocal。
8.4.4 Implementations in OpenGL(在OpenGL中实现)
在OpenGL中使用递归遍历和矩阵栈来处理层次结构的渲染。
为了计算场景中所有的世界矩阵,我们可以使用深度优先遍历来遍历树结构。当遍历到每个节点时,会计算其世界空间矩阵。在遍历到一个节点时,可以保证其父节点的世界矩阵已经可用。OpenGL的矩阵栈被设置用来简化渲染层次场景。在遍历树的过程中,当进入一个新的层级时可以调用glPushMatrix(),而在返回上一层级时可以调用glPopMatrix()。
8.5 Samples and codes(示例和代码)
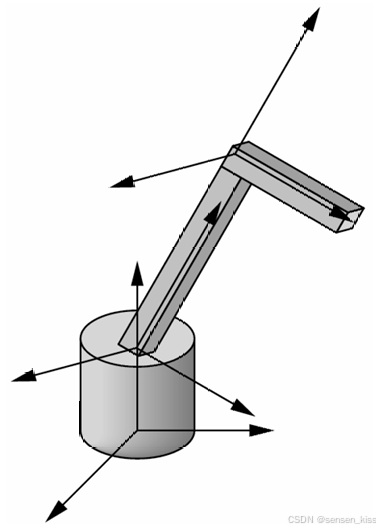
8.5.1 Articulated model – robot arm
机器人手臂是一个关节模型的例子。在机器人手臂中,各个部件通过关节连接在一起。通过指定各个关节的角度,我们可以确定机器人手臂模型的状态。
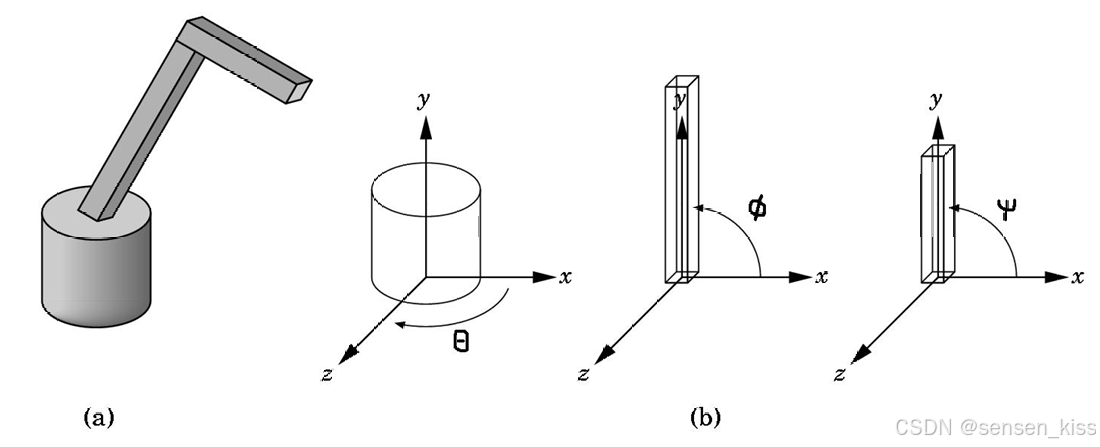
其中
1.基座可以独立旋转,一个单独的角度可以确定它的位置。
2.下臂连接到基座,它的位置取决于基座的旋转。此外,它必须相对于基座进行平移,并围绕连接关节旋转。
3.上臂连接到下臂,它的位置取决于基座和下臂。它必须相对于下臂进行平移,并围绕连接到下臂的关节旋转。
因此
1.基座变换:首先对基座进行旋转操作,得到基座的旋转矩阵
R
b
R_b
Rb,然后将该旋转应用到基座上,得到基座的世界空间矩阵
M
b
−
w
=
R
b
M_{b-w} = R_b
Mb−w=Rb。
2.下臂变换:首先将下臂相对于基座进行平移操作,得到下臂的平移矩阵
T
l
a
T_{la}
Tla,然后围绕连接关节对下臂进行旋转操作,得到下臂的旋转矩阵
R
l
a
R_{la}
Rla,最后将这些变换依次应用到下臂上,得到下臂的世界空间矩阵
M
l
a
−
w
=
M
b
−
w
⋅
M
l
a
=
R
b
⋅
T
l
a
⋅
R
l
a
M_{la-w} = M_{b-w} ⋅ M_{la} = R_b ⋅ T_{la} ⋅ R_{la}
Mla−w=Mb−w⋅Mla=Rb⋅Tla⋅Rla。
3.上臂变换:首先将上臂相对于下臂进行平移操作,得到上臂的平移矩阵
T
u
a
T_{ua}
Tua,然后围绕连接关节对上臂进行旋转操作,得到上臂的旋转矩阵
R
u
a
R_{ua}
Rua,最后将这些变换依次应用到上臂上,得到上臂的世界空间矩阵
M
u
a
−
w
=
M
l
a
−
w
⋅
M
u
a
=
R
b
⋅
T
l
a
⋅
R
l
a
⋅
T
u
a
⋅
R
u
a
M_{ua-w} = M_{la-w} ⋅ M_{ua} = R_b ⋅ T_{la} ⋅ R_{la} ⋅ T_{ua} ⋅ R_{ua}
Mua−w=Mla−w⋅Mua=Rb⋅Tla⋅Rla⋅Tua⋅Rua。
具体代码如下:
void display()
{
glRotatef(theta, 0.0, 1.0, 0.0);
base();
glTranslatef(0.0, h1, 0.0);
glRotatef(phi, 0.0, 0.0, 1.0);
lower_arm();
glTranslatef(0.0, h2, 0.0);
glRotatef(psi, 0.0, 0.0, 1.0);
upper_arm();
}
此时上臂的ModelVIEW矩阵是
M
u
a
−
w
=
R
b
(
θ
)
⋅
T
l
a
(
h
1
)
⋅
R
l
a
(
φ
)
⋅
T
u
a
(
h
2
)
⋅
R
u
a
(
ψ
)
M_{ua-w} = R_b(θ) ⋅ T_{la}(h_1) ⋅ R_{la}(φ) ⋅ T_{ua}(h_2) ⋅ R_{ua}(ψ)
Mua−w=Rb(θ)⋅Tla(h1)⋅Rla(φ)⋅Tua(h2)⋅Rua(ψ)
如果信息储存在节点中(而不是在边缘中),每个节点至少需要存储以下信息:指向绘制节点所表示对象的函数的指针。一个矩阵,用于相对于节点的父节点定位、定向和缩放节点对象(包括其子节点)。指向其子节点的指针。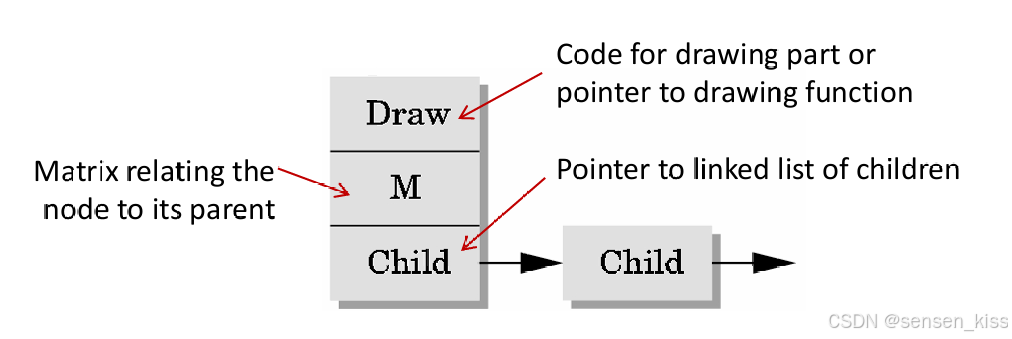
8.5.2 A humanoid model
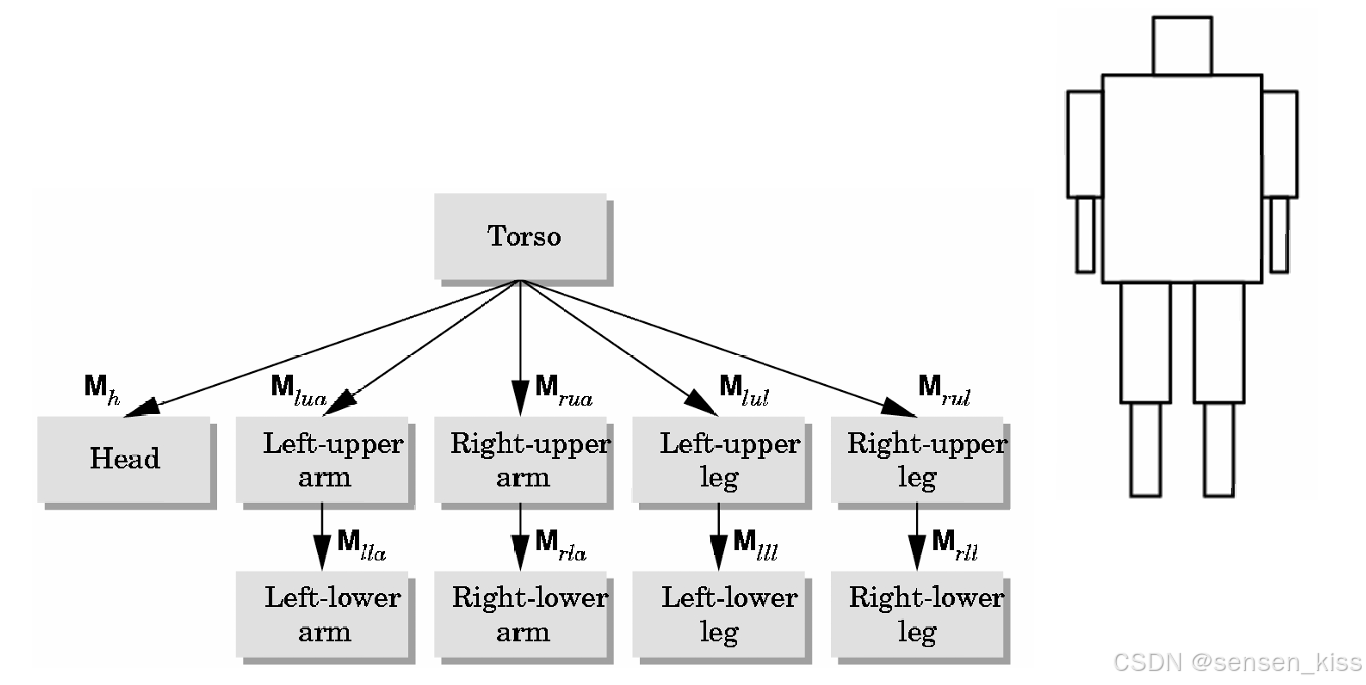
现在我们尝试构建一个简单的人形模型,使用椭球体和圆柱体等简单的几何图形来实现。我们可以通过一些函数来访问不同的部分,比如torso()表示躯干,left_upper_arm()表示左上臂等。还可以用矩阵来描述节点相对于其父节点的位置。例如
M
l
l
a
M_{lla}
Mlla描述了左下臂相对于左上臂的位置。
在这个人形模型中,人物的姿势由11个关节角度决定。这个树状结构的模型可以被视为一种图遍历过程。遍历每个节点一次,这可以被视为一种图的遍历过程,确保每个部分都被正确处理。在访问每个节点时,执行与该节点相关联的显示函数,这个函数描述了该节点表示的部分,并应用正确的变换矩阵来设置位置和方向。
所有矩阵都是增量的,可以使用任何遍历算法(深度优先或广度优先)。可以从左到右并且深度优先遍历。在代码中进行显式遍历,使用栈来存储所需的矩阵和属性。递归遍历代码更简单,并且矩阵和属性的存储是隐式的。
用于人形模型的变换矩阵,这些变换矩阵用于描述不同部分相对于其父部分的位置和方向关系。一共有10个相关的矩阵:
1.
M
t
M_t
Mt用于描述整个人物模型相对于躯干的位置和方向关系,因为躯干是根节点。
2.
M
h
M_h
Mh用于描述头部相对于躯干的位置和方向关系。
3.
M
l
u
a
,
M
r
u
a
,
M
l
u
l
,
M
r
u
l
M_{lua}, M_{rua}, M_{lul}, M_{rul}
Mlua,Mrua,Mlul,Mrul用于描述四肢(手臂和腿)相对于躯干的位置和方向关系。
4.
M
l
l
a
,
M
r
l
a
,
M
l
l
l
,
M
r
l
l
M_{lla}, M_{rla}, M_{lll}, M_{rll}
Mlla,Mrla,Mlll,Mrll用于描述四肢的下半部分相对于相应的上半部分(父节点)的位置和方向关系。
绘制步骤如下:
1.将模型-视图矩阵
M
M
M设置为
M
t
M_t
Mt,并绘制躯干。
2.将模型-视图矩阵
M
M
M设置为
M
t
⋅
M
h
M_t ⋅ M_h
Mt⋅Mh,并绘制头部。
3.对于左上臂,需要使用
M
t
⋅
M
l
u
a
M_t ⋅ M_{lua}
Mt⋅Mlua等等。
4.不必重新计算
M
t
⋅
M
l
u
a
M_t ⋅ M_{lua}
Mt⋅Mlua等矩阵,也不必使用逆矩阵,而是可以使用矩阵堆栈来存储
M
t
⋅
M
l
u
a
M_t ⋅ M_{lua}
Mt⋅Mlua等矩阵,以及在遍历树状结构时所需的其他矩阵。
注意左下臂的model-view矩阵是
M
l
l
a
−
w
=
M
t
⋅
M
l
u
a
⋅
M
l
l
a
M_{lla-w} = M_t ⋅ M_{lua} ⋅ M_{lla}
Mlla−w=Mt⋅Mlua⋅Mlla
简化的示例代码如下。
void figure() {
torso();
glPushMatrix(); // save present MODELVIEW matrix
glTranslatef(); // update MODELVIEW matrix for the head
glRotate3();
head();
glPopMatrix(); // recover MODELVIEW matrix for the
// torso and save the state
glPushMatrix();
glTranslatef(); // update MODELVIEW matrix for
glRotate3(); // the left upper leg
left_upper_leg();
glTranslatef();
glRotate3(); // incremental change for
left_lower_leg(); // the left_lower_leg
glPopMatrix(); // recent state recovery
...;
}
下面的代码定义了一个树状数据结构用来表示人形模型的各个部分。
typedef struct treenode
{
GLfloat m[16];
void(*f)();
struct treenode *sibling;
struct treenode *child;
} treenode;
...
treenode torso_node,
head_node,
...;
下面的代码定义了人形模型的躯干部分,并为其创建了一个树状数据结构节点。
// for the torso
glRotatef(theta[0], 0.0, 1.0, 0.0);
glGetFloatv(GL_MODELVIEW_MATRIX, torso_node.m);
// matrix elements copied to the M of the node
// the torso node has no sibling; and
// the leftmost child is the head node
// rest of the code for the torso node
torso_node.f = torso;
torso_node.sibling = NULL;
torso_node.child = &head_node
同理,对于上臂部分来说。
// for the upper-arm node
glTranslatef(-(TORSO_RADIUS+UPPER_ARM_RADIUS),
0.9*TORSO_HEIGHT, 0.0)
glRotatef(theta[3], 1.0, 0.0, 0.0);
glGetFloatv(GL_MODELVIEW_MATRIX, lua_node.m);
// matrix elements copied to the m of the node
lua_node.f = left_upper_arm;
lua_node.sibling = &rua_node;
lua_node.child = &lla_node;
由于我们使用树状结构存储,我们现在还需要一个遍历树状数据结构的方法,代码如下。
// assumption MODELVIEW state
void traverse(treenode* root);
{
if(root==NULL) return;
glPushMatrix();
glMultMatrixf(root->m);
root->f();
if(root->child!=NULL) traverse(root->child);
glPopMatrix();
if(root->sibling!=NULL) traverse(root->sibling);
} // traversal method is independent of the
// particular tree!
在遍历树状数据结构时需要注意的一些细节和最佳实践:在应用节点矩阵之前,需要保存当前的模型视图矩阵状态(使用 glPushMatrix)。这是因为应用节点矩阵后,可能需要对其子节点进行相对变换,而这些相对变换是基于当前的模型视图矩阵状态计算的。
更新的矩阵只适用于当前节点的子节点,而不适用于其兄弟节点。因此,在遍历完子节点后,需要返回到之前保存的模型视图矩阵状态(使用 glPopMatrix),然后再遍历兄弟节点。
如果在节点的渲染函数中有改变属性的操作,可以选择在渲染函数内部使用 glPushAttrib 和 glPopAttrib 来保存和恢复属性状态,或者在遍历节点时,将属性状态与模型视图矩阵状态一起保存和恢复。
最后用一个回调函数将前面的零件组装在一起。
// generic display callback function
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT |
GL_DEPTH_BUFFER_BIT);
glLoadIdentity();
traverse(&torso_node);
glutSwapBuffers();
}
可以通过鼠标或键盘控制关节角度的变化,从而实现对人形模型的动态动画效果。























 684
684

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








