反卷积与棋盘效应

最新推荐文章于 2022-05-12 10:51:16 发布

灰巧克力爱松露

最新推荐文章于 2022-05-12 10:51:16 发布

阅读量8.6k

点赞数 4

分类专栏： Deep Learning 文章标签：上采样反卷积网络棋盘效应图像生成

本文链接：https://blog.csdn.net/shadow_guo/article/details/52862161

版权

Deep Learning 专栏收录该内容

23 篇文章 1 订阅

订阅专栏

来自 Google Brain 的 Augustus Odena 等人的文章“Deconvolution and Checkerboard Artifacts“的部分内容 1。

1. 更好的上采样

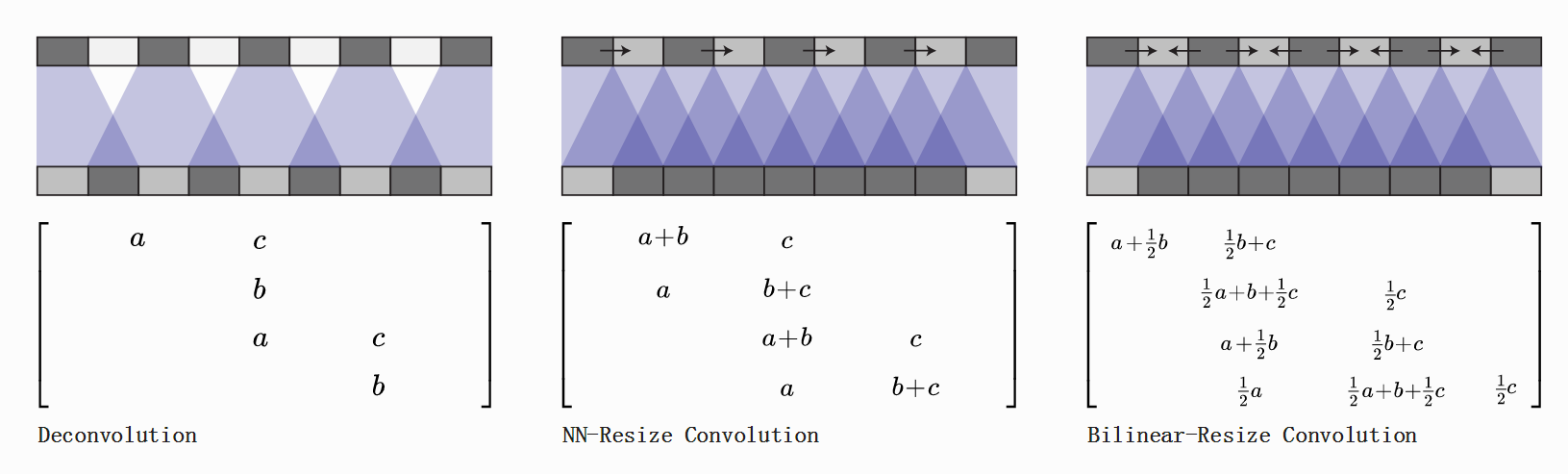
图像生成网络的上采样部分通常用反卷积网络，不合理的卷积核大小和步长会使反卷积操作产生棋盘效应 (checkerboard artifacts)。

为避免棋盘效应，有两种方法可替换常规的反卷积（卷积的转置）。与反卷积不同，上采样方法本身不应有棋盘效应。理想的方法将会更远离棋盘效应。

直观地看，假设生成的图像中包含1只黑猫。黑猫身体部分的像素颜色应平滑过渡，或极端地说，该部分应全为黑色。实际生成的图像中该部分却有深深浅浅的近黑方块组成，很像棋盘的网格，即棋盘效应。

第一种方法是用到的反卷积核的大小可被步长整除，从而避免重叠效应。与最近成功用于图像超分辨率的技术“子像素卷积”（sub-pixel convolution）等价。

另一种方法是从卷积操作中分离出对卷积后更高分辨率的特征图上采样来计算特征。例如，可以先缩放图像（最近邻插值或双线性插值），再卷积。貌似是个自然的方法。

反卷积与不同缩放卷积方法都是线性操作，并可用矩阵去解释。对于每个输出窗口，反卷积操作的输入唯一，缩放卷积会以阻碍高频棋盘效应的方式来隐式地集中权重（weight-tying）。

后面为猜测部分。

2. 反卷积

从反卷积矩阵 $\left[\begin{matrix}a&c\\&b\\&a&c\\&&b\end{matrix}\right]$ 来看，卷积应该为 $\left[\begin{matrix}a&0\\c&b\end{matrix}\right]$ ，则卷积的转置为 $\left[\begin{matrix}a&c\\0&b\end{matrix}\right]$ ；步长为2，可整除反卷积大小。

3. 缩放卷积

缩放卷积为线性操作：假设原图像为 $A$ ，经过插值后的图像为 $A+B$ ；用卷积核 $C$ 对插值缩放后的图像卷积，得到最终的图像 $C^T*(A+B)=C^T*A+C^T*B$ ，其中 $*$ 为卷积操作。则可将缩放卷积分解为原图像卷积和插值增量图像卷积，或卷积的原图像和卷积的插值增量图像。

$C$ 为卷积操作的卷积核。此时为上采样，理解为反卷积操作中的卷积核。

(1) 最近邻缩放卷积

$⎡ ⎣ ⎢ ⎢ ⎢ a + b a c b + c a + b a c b + c ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ a c b a c b ⎤ ⎦ ⎥ ⎥ ⎥ + ⎡ ⎣ ⎢ ⎢ ⎢ b a c b a c ⎤ ⎦ ⎥ ⎥ ⎥$ $\left[\begin{matrix}a+b&c\\a&b+c\\&a+b&c\\&a&b+c\end{matrix}\right]=\left[\begin{matrix}a&c\\&b\\&a&c\\&&b\end{matrix}\right]+\left[\begin{matrix}b\\a&c\\&b\\&a&c\end{matrix}\right]$

发现，插值增量图像表示的矩阵为原图像表示的矩阵下移1行。可将原图像矩阵看成环形队列（队列最后1行的输出送入队列的第1行）。

(2) 双线性缩放卷积

$⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ a + b 2 a 2 (?) c + b 2 b + c 2 + a 2 a + b 2 a 2 c 2 c + b 2 b + c 2 + a 2 c 2 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ a c b a c b ⎤ ⎦ ⎥ ⎥ ⎥ + ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ b 2 a 2 (?) c 2 b 2 a 2 c 2 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ + ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ b 2 a 2 c 2 b 2 a 2 c 2 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥$ $\begin{align} &\left[\begin{matrix}a+\frac{b}{2}&c+\frac{b}{2}\\\frac{a}{2}(?)&b+\frac{c}{2}+\frac{a}{2}&\frac{c}{2}\\&a+\frac{b}{2}&c+\frac{b}{2}\\&\frac{a}{2}&b+\frac{c}{2}+\frac{a}{2}&\frac{c}{2}\end{matrix}\right]\\ &=\left[\begin{matrix}a&c\\&b\\&a&c\\&&b&\end{matrix}\right] +\left[\begin{matrix}\frac{b}{2}\\\frac{a}{2}(?)&\frac{c}{2}\\&\frac{b}{2}\\&\frac{a}{2}&\frac{c}{2}&\end{matrix}\right] +\left[\begin{matrix}&\frac{b}{2}&&\\&\frac{a}{2}&\frac{c}{2}\\&&\frac{b}{2}\\&&\frac{a}{2}&\frac{c}{2}\end{matrix}\right] \end{align}$

发现，插值增量图像可细分为原图像表示的矩阵下移1行后乘以 $\frac{1}{2}$ 与原图像表示的矩阵上移1行后乘以 $\frac{1}{2}$ 。

4. 注意

(?)部分的元素为原文中的矩阵的缺失部分。所以，可能仍未理解 Augustus Odena 的本意。有误导之嫌，仅供娱乐~ Σ(⊙▽⊙”a