模式识别学习笔记：第八章特征提取

最新推荐文章于 2024-08-23 10:28:43 发布

mingo_敏

最新推荐文章于 2024-08-23 10:28:43 发布

阅读量1.1w

点赞数 2

分类专栏： CV/PR 模式识别学习笔记文章标签：模式识别脸部识别

本文链接：https://blog.csdn.net/shanglianlm/article/details/49468797

版权

CV/PR 同时被 2 个专栏收录

16 篇文章 7 订阅

订阅专栏

模式识别学习笔记

5 篇文章 20 订阅

订阅专栏

本系列博客主要是在学习《模式识别（张学工著第三版）》时的一些笔记。
本文地址：http://blog.csdn.net/shanglianlm/article/details/49468797

1 引言

1-1 问题

从 D 个特征中选出 d (< D) 个新特征。

1-2 目的

降低特征空间的维数，使后续分类器设计在计算上更容易实现；
为了消除特征之间可能存在的相关性，减少特征中与分类信息无关的信息，使新特征更有利于分类。

1-3 公式

线性： $y = W^{T}x$
非线性： $y = W(x)$

2 基于类别可分性判据的特征提取

采用前面第七章中介绍的类别可分性判据作为衡量新特征的准则，则特征提取的问题就是求最优的 $W^{*}$ ，使

这里写图片描述

其中 J 为类别可分性判据。

这里写图片描述

3 主成分分析方法（PCA）

目的：从原特征组中计算出一组按重要性从大到小排列的新特征，它们是原有特征的线性组合，并且相互之间是不相关的。

协方差矩阵计算的是不同维度之间的协方差，而不是不同样本之间的。

求协方差矩阵matlab代码：

data = rand(m, n);
X = data – repmat(mean(data), m, 1);    % 中心化样本矩阵
C = (X'*X)./(size(X,1)-1)

应用
- 降维后分类（不一定有利）或聚类。
- 去噪。

关于PCA的一个链接 PCA （主成分分析）详解（写给初学者）结合matlab

4 Karhunen-Loeve变换

基本原理和 PCA 类似，但 K-L 变换能够考虑到不同的分类信息，实现监督的特征提取。

4-1 K-L变换

这里写图片描述

4-2 性质：

K-L 是信号的最佳压缩表示（损失最小）；
K-L 变换的新特征是互不相关的，新特征向量的二阶矩阵是对角阵，对角阵元素就是 K-L 变换中的本征值。
K-L 坐标系用来表示原数据，表示熵最小（样本的方差信息最大程度地集中在较少的维数上）。
如果用本征值最小的 K-L 变换坐标来表示原数据，则总体熵最小（在这些坐标上的均值能够最好地代表样本集）。

4-3 与 PCA 关系

K-L得到的 d 个新特征与 PCA 中的 d 个主成分很相似，当原特征为零均值或者对原特征值进行去均值处理后，二者就等价了。

4-4 用于监督模式识别的 K-L 变换

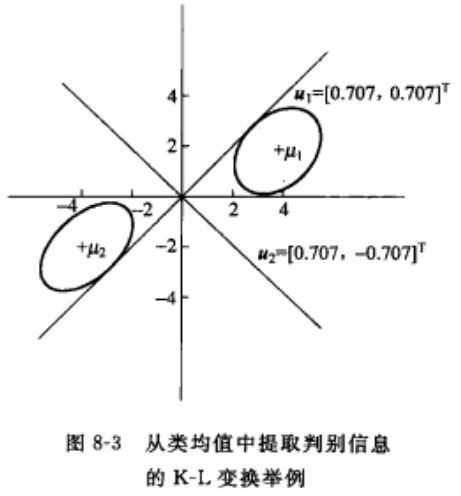
这里写图片描述

4-4-1 从类均值中提取判别信息

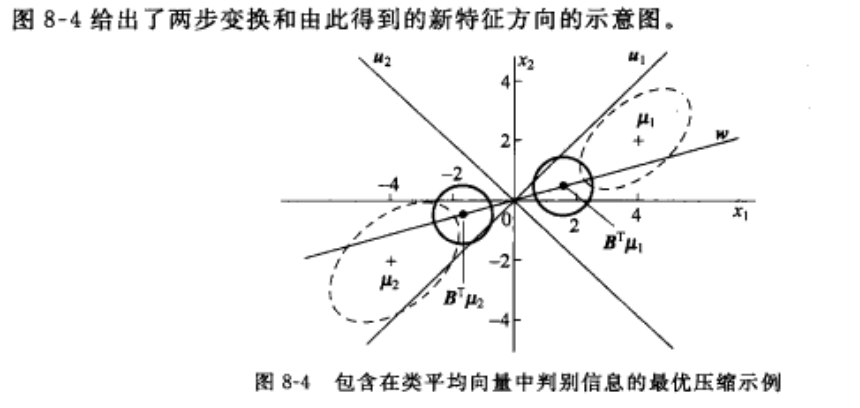
这里写图片描述

实例
这里写图片描述

4-4-2 包含在类平均向量中判别信息的最优压缩

如果要用最少的维数来保持原空间中类平均向量中的信息，则可以在是特征间互不相关的前提下最优压缩均值向量中包含的分类信息。

这里写图片描述

4-4-3 类中心化特征向量中分类信息的提取

如果把各类样本都减去各自的均值，就消除了各类均值差别所包含的分类信息。这时，如果各类的分布形状不同，仍然能从各类的协方差中提取出分类信息。

这里写图片描述

4-5 K-L变换在人脸识别中的应用举例（eigenface 方法）

eigenface 方法： Eigenfaces for recognition

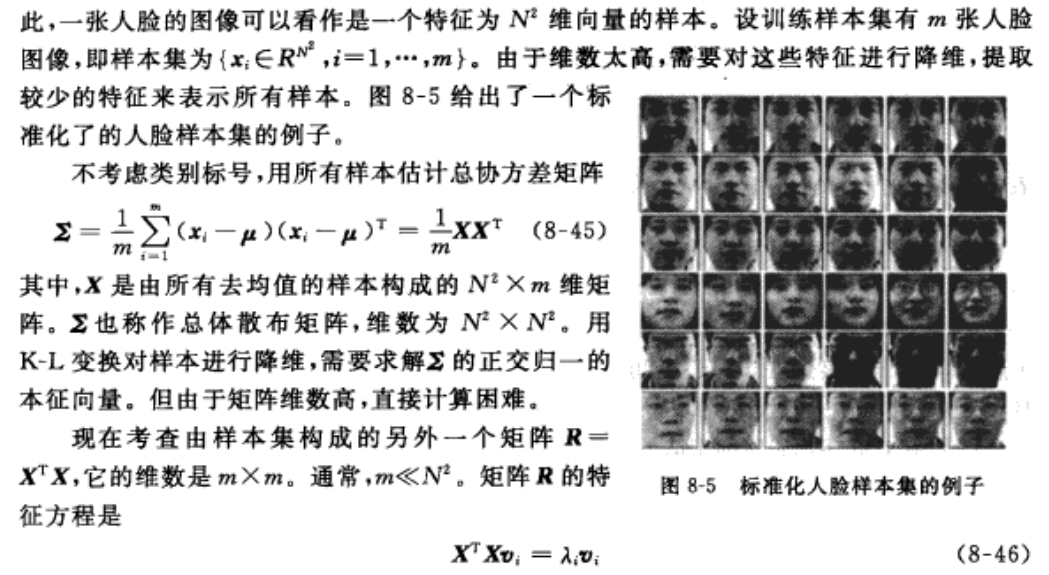
这里写图片描述

三个要点：
1. $XX^{T}$ 的维数较大时，特征值难计算，考虑先计算 $X^{T}X$ 的，然后变过来。
2. 通过控制最后提取的特征值占所有特征值的比重，来确定本征脸的个数。
3. 其他图像的特点与人脸不同，所以也可以用来做人脸检测。
4.
这里写图片描述

5 高维数据的低维显示

当数据在高维空间中时，通过线性变换在二维（或三维）空间内反映数据的分布，叫做数据的低维可视化。
例如使用 PCA 映射到二维或者取主成分的前几维。

6 非线性变换方法

当数据在高维空间中具有复杂的分布时，通过线性变换在二维（或三维）空间内反映数据的分布会有很大的局限性。

6-1 核主成分分析（KPCA）

6-1-1 基本思想

对样本进行非线性变换，通过在变换空间进行主成分分析来实现在原空间的非线性主成分分析。利用可再生希尔伯特空间的性质，在变换空间中的协方差矩阵可以通过原空间中的核函数进行运算，从而绕开了复杂的非线性变换。

6-1-2 具体算法

这里写图片描述

6-1-3 特点

这里写图片描述

6-2 IsoMap方法

这里写图片描述

Isomap的优点在于：
1. 求解过程依赖于线性代数的特征值和特征向量问题，保证了结果的稳健性和全局最优性；
2. 能通过剩余方差判定隐含的低维嵌入的本质维数；
3. Isomap方法计算过程中只需要确定唯一的一个参数（近邻参数k或邻域半径e）。

[1] A Global Geometric Framework for Nonlinear Dimensionality Reduction

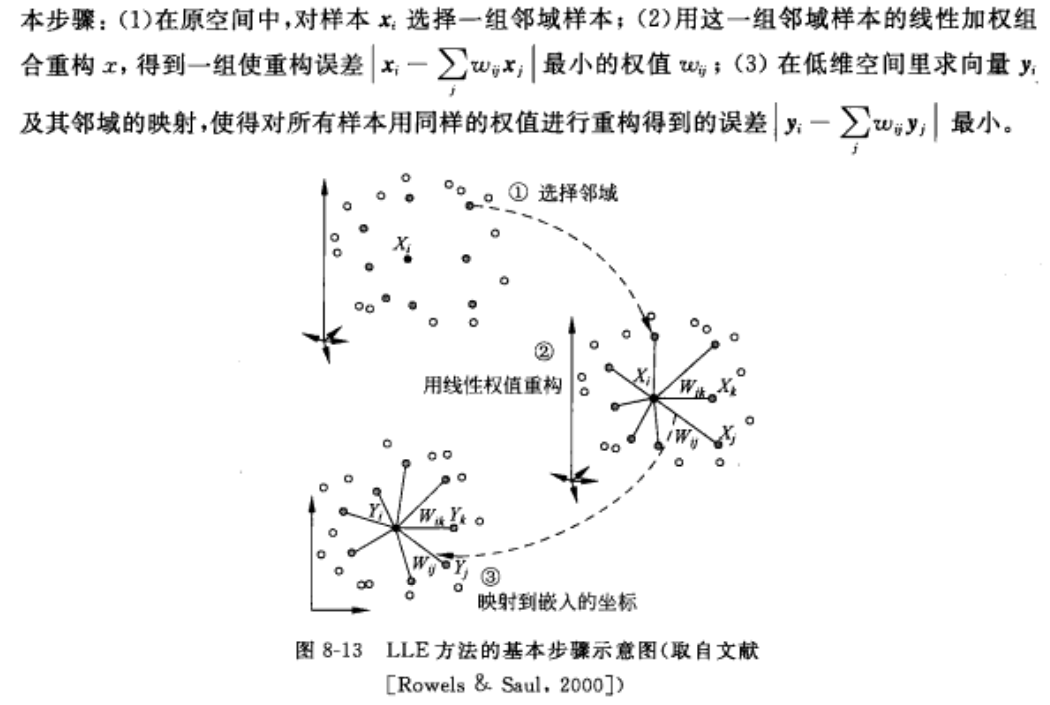
6-3 LLE 方法

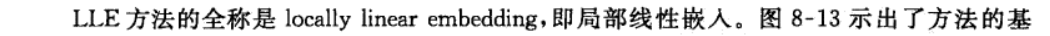
这里写图片描述

[1] Locally Linear Embedding

6-4 多维尺度法（MDS）

6-4-1 古典尺度法

与PCA类似，多维尺度分析(MDS)的目的也是把观察的数据用较少的维数来表达。然而，MDS利用的是成对样本间相似性构建合适的低维空间，使得样本在此空间的距离和在高维空间中的样本间的相似性尽可能的保持一致。

MDS 的出发点并不是把样本从一个空间映射到另外一个空间，而是为了根据样本之间的距离关系或不相似度关系在低维空间里生成对样本的一种表示。

6-4-2 古典尺度法（主坐标分析 principal coordinates analysis）

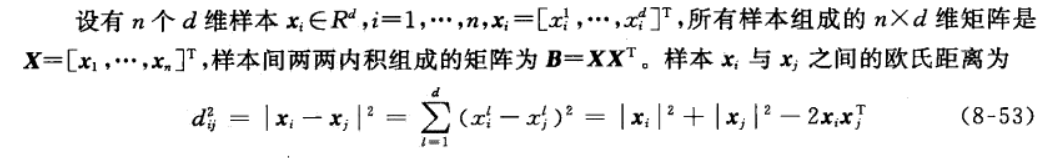
这里写图片描述

6-4-3 度量型 MDS

这里写图片描述

6-4-4 非度量型 MDS

与度量型 MDS 的差异：
- 也叫做顺序 MDS。
- 度量型 MDS 只有定性意义，非度量型 MDS 有定性意义和定量意义（A与B比A与C更相似）。
- 也需要最小化式（8-61）或式（8-63）形式的目标函数，但是其中的函数 $\phi ()$ 或 $f()$ 只需要是某种单调函数或弱单调函数即可。