线性代数之特征值与特征向量的求法

                           线性代数之特征值与特征向量的求法

特征值与特征向量

已知如下矩阵A，求解其特征值和特征向量。

首先构造特征方程 det(λE-A)

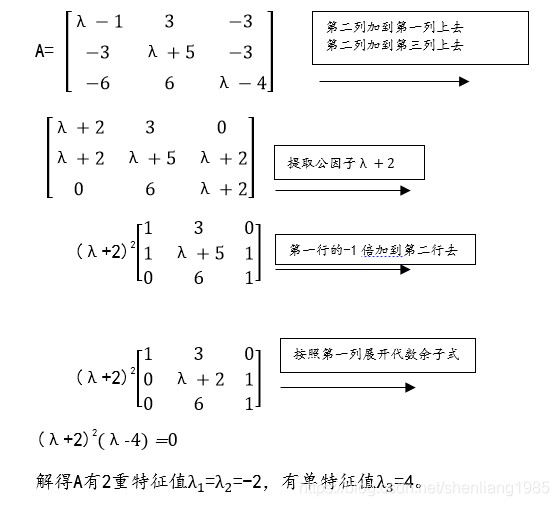
情况一:

特征值 = =-2时解方程组(-2E-A)X=0，即得：

于是得同解方程组 - + =0，解为 = - (这里 , 为自由未知量)。

分别令自由未知量 = , = 
进而得到基础解系为：

情况二：

特征值 =4时解方程组(4E-A)X=0，即得

总结

Step1：先构造特征方程、展开特征多项式，求出特征值。

Step2：对得到的特征值分别带入原矩阵并化简为行简化型

Step3：求出对应行简化型对应的基础解系并通过通解表示出特征向量