博弈论学习笔记

博弈论学习笔记

---

一、博弈论（Game Theory)介绍

起源：《孙子兵法》最早的一部博弈论专著，但没有理论化

关键人物：冯·诺依曼，博弈论之父，《博弈论与经济行为》证明了博弈论基本原理

关键人物：约翰·纳什，纳什均衡的概念和均衡存在定理

贴近生活的应用：买衣服；古董买卖；人工智能

什么是博弈论？

在一定游戏规则约束下，基于直接相互作用的条件下，各参与人依据所掌握的信息，选择各自的策略，以实现利益最大化的过程。

博弈分类：

1.是否合作：合作博弈；非合作博弈（静态博弈，动态博弈）

2.对博弈各方信息掌握不同：完全信息博弈；非完全信息博弈

基本假设：

1. 人是理性假设
2. 共同知识假设（参与者在无穷递归意义上均知悉的事实）：信息不对称的情况下，博弈的结果不取决于大家怎么想，而取决于大家认为大家怎么想

二、囚徒困境：

两个共同犯罪的人（张三和李四）被关进监狱，不能相互沟通情况。如果两个人都不揭发对方，则由于证据不确定，每个人都坐牢半年，若一个人揭发，而另一个人沉默，则揭发者因为立功而立即获释，沉默者因不合作而入狱五年；若相互揭发，则因证据确凿，二者都判刑三年。

前面数字为张三坐牢时间，后面数字为李四坐牢时间。

假设李四选择揭发，则张三选择揭发坐牢时间更短；假设李四选择沉默，则张三选择揭发同样坐牢时间更短；所以无论李四怎么选择，张三选择揭发都收益最大。由于囚徒无法信任对方，因此倾向于互相揭发，而不是同守沉默。

囚徒困境产生的原因：

1.双方都有占优策略

a1>a3,a2>a4时，张三选择揭发占优；

b1>b3,b2>b4时，李四选择揭发占优；

2.有一个合作解，使双方收益都优于其在占优策均衡下的收益

即：a1<a4,b2<b4，如果双方合作，会有更好地结果。

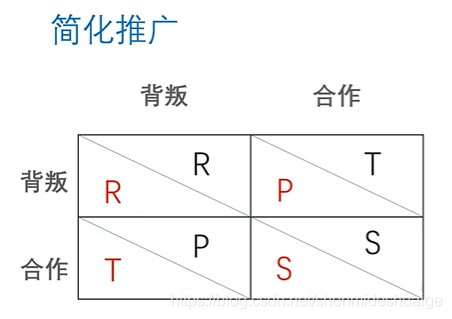
两人双策略对称博弈，满足P>S>R>T，则选择个人占优策略（R,R）构成囚徒困境。

原因：个人理性与集体非理性

如何破解囚徒困境？打破囚徒困境形成条件

1. 不只为自己着想，考虑大家的利益
2. 相互有信息沟通，打破猜疑和信息茧房

三、纳什均衡

基本概念：

策略集合：策略集合是由玩家能够实行的策略所组成的集合。例如游戏剪刀石头布的策略集合是{出剪刀；出石头；出布}

收益矩阵：玩家在游戏中，每一个策略所对应的收益所组成的矩阵

小鸡游戏：

1. 甲和乙的策略集合都是{选鸡；选鹰}
2. 显然，这个游戏最好的结果是甲和乙同时选择“鸡”，这样他们两个都可以得4分
3. 但是，如果甲选“鸡”的话，乙应该选“鹰”，这样他可以得5分而不是4分。我们把乙当他知道甲选“鸡”的时候选“鹰”，称为他的一个最优策略，反之亦然

纳什均衡：在博弈中，如果每个参与者在已知其他参与者策略的情况下，采用最优策略应对，那么我们就达到了一个纳什均衡，或者找到了一个纳什均衡解，同时也意味着没有人能够通过改变自己的策略，获得更好的结果。

在小鸡游戏中，明显（鸡，鹰）和（鹰，鸡）是纳什均衡。

纯策略纳什均衡：参与者只能使用策略集合中的一条策略

• （纯）纳什均衡可以存在多个，也可能不存在
• 以小鸡游戏为例，对于甲和乙来说，他们分别的策略集合只包含了{选鸡，选鹰}两个策略。在纯策略纳什均衡下，他们只能使用其中的一条策略

混合策略纳什均衡：没有人能通过改变自己的混合策略，获得更好地结果，即在混合策略纳什均衡下，参与者无法通过改变自己的组合策略而获利。

混合策略是以某种概率选择策略集合中的不同的策略。

例如：假设策略集合，

• 纯策略的策略是只选择S1，选择其他策略的概率为0，即

• 混合策略的策略是有一半概率选择S1，一半概率选择S2，选择策略S3的概率为0，即

• 混合策略的策略是选择每个策略的概率都是1/3，即

---