Puzzle框架：基于NAS的推理优化LLM的突破性贡献

Puzzle框架：基于NAS的推理优化LLM的突破性贡献

近年来，大型语言模型（LLM）的性能显著提升，但其高昂的推理成本限制了广泛应用。NVIDIA团队在论文《PUZZLE: DISTILLATION-BASED NAS FOR INFERENCE-OPTIMIZED LLMS》中提出了Puzzle框架，通过神经架构搜索（NAS）和知识蒸馏技术，优化LLM的推理效率，同时保留其性能。本博客面向深度学习研究者，详细剖析Puzzle框架的贡献及其核心原理。

Paper： https://arxiv.org/pdf/2411.19146

主要贡献

Puzzle框架针对LLM推理优化的痛点，提出了一系列创新方法，其贡献可归纳为以下四点：

1. 提出分解式NAS框架：Puzzle首次将分解式NAS大规模应用于LLM，探索数十亿参数模型的架构空间，优化硬件特定约束（如吞吐量、延迟、内存）。通过块级本地蒸馏（BLD）和混合整数规划（MIP），Puzzle显著降低训练成本，仅需不到50B token即可完成优化，相比原始模型的15T token大幅减少。

2. 推出高效模型Nemotron-51B：基于Llama-3.1-70B-Instruct，Puzzle衍生出Llama-3.1-Nemotron-51B-Instruct模型，在单块NVIDIA H100 GPU上实现2.17倍推理吞吐量提升，同时保留98.4%的原始性能。该模型针对FP8量化和非均匀架构优化，树立了商业应用的效率标杆。

3. 优化真实推理场景：Puzzle针对实际推理引擎和量化水平（如FP8）优化，增强了TensorKT-LLM支持非均匀块和变头数注意力机制。这种硬件感知优化确保模型在真实部署场景中的高效性和成本效益。

4. 提供架构与硬件效率分析：Puzzle通过实证分析揭示了架构选择与硬件效率的关系，为未来硬件感知LLM设计提供了指导性洞见。

核心原理

Puzzle框架通过三个阶段实现推理优化：块级本地蒸馏（BLD）、MIP架构搜索和全局知识蒸馏（GKD）。以下逐一解析其原理。

1. 块级本地蒸馏（BLD）

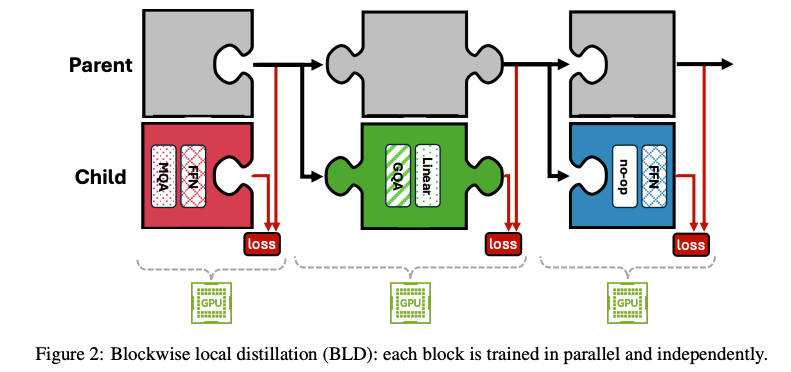
原理：BLD通过分解式NAS为每个变换器层（block）构建一个子块库，包含多种注意力（attention）和前馈网络（FFN）变体。每个子块独立训练以模仿其对应的父模型块，采用归一化均方误差（MSE）损失：

$$\mathcal{L}=\frac{\text{MSE}(a_p,a_c)}{\text{MSE}(a_p,0)}$$

其中，($a_p$) 和 ($a_c$) 分别表示父块和子块的输出。这种本地化训练隔离了块间依赖，允许并行训练，显著降低计算成本。

创新点：

• 解耦BLD：相比耦合BLD（训练所有注意力-FFN组合），解耦BLD仅训练注意力或FFN变体与冻结父子块的组合。例如，对于 ($m$) 个注意力变体、($n$) 个FFN变体和 ($l$) 个层，耦合BLD需训练 ($m\cdot n\cdot l$) 个变体，而解耦BLD仅需 ($(m+n)\cdot l$) 个，效率提升显著。
• 初始化优化：通过基于激活的通道贡献（Channel Contribution）方法初始化FFN子块，优先修剪低贡献通道；注意力子块通过均值池化或投影矩阵乘积初始化，加速蒸馏收敛。

优势：BLD仅需约1B token的小数据集即可完成训练，且无需父模型的原始训练数据，适用于“开放权重、封闭数据”场景。

2. 混合整数规划（MIP）架构搜索

原理：MIP在BLD生成的子块库中搜索最优架构，满足特定硬件约束（如内存、延迟、吞吐量）。Puzzle首先测量每个子块在目标硬件上的资源需求（如预填充和生成阶段的延迟），然后通过MIP优化算法选择子块组合，最大化模型性能。

创新点：

• 硬件感知优化：直接测量目标硬件（如H100 GPU）上的运行时和内存需求，考虑批大小、序列长度和量化水平（如FP8），克服了FLOPs等理论指标的局限性。
• 非均匀架构：Puzzle生成的模型（如Nemotron-51B）采用非均匀架构，部分层减少或跳过注意力/FFN操作，优化资源分配，提升硬件利用率。

优势：MIP阶段无需为每个候选架构进行全模型蒸馏，仅在最终架构确定后进行GKD，显著降低搜索成本。

3. 全局知识蒸馏（GKD）

原理：由于BLD独立训练子块，可能导致块间不兼容，GKD通过全局蒸馏微调整个模型，修复误差传播问题。GKD使用父模型指导子模型，确保性能接近原始模型。

优势：GKD仅在最终架构上执行，结合BLD的低成本特性，使整个框架高效可扩展。

搜索空间设计

Puzzle定义了丰富的搜索空间，涵盖每个变换器层的注意力子块（(${\mathcal{A}}_i$)）和FFN子块（(${\mathcal{F}}_i$)）变体：

• 注意力子块：包括分组查询注意力（GQA，变体为8、4、2、1个键值头）、线性层或空操作（no-op）。
• FFN子块：包括完整中间维度、约87%、75%、50%、25%、20%、10%的缩减维度、线性层或空操作。

以Llama-3.1-70B（80层）为例，每层有6种注意力变体和9种FFN变体，共54种配置，总搜索空间达 ($54^{80}\approx 10^{118}$)。这种多样性允许Puzzle灵活平衡计算成本和表示能力。

实证结果与洞见

• 效率突破：Nemotron-51B在H100 GPU上实现2.17倍吞吐量提升，内存效率显著提高，适合大批量推理场景。
• 性能保留：在RULER基准测试中，Nemotron-51B保留了98.4%的父模型性能，尤其在长上下文任务中表现优异。
• 硬件效率分析：Puzzle揭示了批大小对生成阶段硬件利用率的关键影响，强调实际测量优于理论指标。

未来方向

Puzzle框架为LLM推理优化开辟了新路径，未来可探索：

• 更复杂的搜索算法（如强化学习或进化算法）。
• 架构模式与特定任务能力的关系。
• 动态架构适配以应对分布变化或新任务。

结论

Puzzle框架通过分解式NAS、BLD和MIP，实现了LLM推理效率的突破性提升。其硬件感知优化和低成本特性使其在商业部署中具有巨大潜力。Nemotron-51B的成功验证了非均匀架构在实际场景中的优势，为深度学习研究者提供了宝贵的参考。

块级本地蒸馏

以下是对块级本地蒸馏（BLD）部分的详细解析，重点回答你的问题，包括损失函数分母的含义、解耦BLD的原理与效率、潜在的选择空间损失，以及基于激活的通道贡献（Channel Contribution）方法的细节。内容将深入技术细节，同时保持清晰易懂，面向深度学习研究者。

---

1. 损失函数中的分母 ($\text{MSE}(a_p,0)$) 的含义

公式背景：
Puzzle框架在BLD阶段通过归一化均方误差（MSE）损失训练每个子块（child block）以模仿对应的父块（parent block）。损失函数定义为：

$$\mathcal{L}=\frac{\text{MSE}(a_p,a_c)}{\text{MSE}(a_p,0)}$$

其中：

• ($a_p$)：父块的输出，表示父模型在对应变换器层的激活值。
• ($a_c$)：子块的输出，表示当前训练的候选子块的激活值。
• ($\text{MSE}(a_p,a_c)=\frac{1}{n}{\sum }_{i=1}^n(a_p^{(i)}-a_c^{(i)}{)}^2$)：父块输出与子块输出之间的均方误差，衡量子块模仿父块的准确性。
• ($\text{MSE}(a_p,0)=\frac{1}{n}{\sum }_{i=1}^n(a_p^{(i)}-0{)}^2=\frac{1}{n}{\sum }_{i=1}^n(a_p^{(i)}{)}^2$)：父块输出与零向量之间的均方误差，等价于父块输出的二范数平方。

分母 ($\text{MSE}(a_p,0)$) 的含义：

• 分母 ($\text{MSE}(a_p,0)$) 是一个归一化因子，代表父块输出 ($a_p$) 的能量（或信号强度）。它计算的是父块输出的平方和，反映了父块输出相对于“零输出”的偏差。
• 通过除以 ($\text{MSE}(a_p,0)$)，损失函数将分子 ($\text{MSE}(a_p,a_c)$) 归一化为相对误差。这种归一化有以下作用：
  1. 尺度无关性：不同层的父块输出可能有不同的量级（例如，由于激活值的分布或层的深度差异）。归一化消除了这种尺度差异，使损失函数在所有层上具有可比性。
  2. 稳定训练：归一化后的损失值通常在 [0, 1] 范围内（因为 ($\text{MSE}(a_p,a_c)\le \text{MSE}(a_p,0)$) 在大多数情况下成立），这有助于稳定梯度更新，允许使用更高的学习率。
  3. 物理意义：分母表示“如果子块输出全为零时的误差”，因此损失函数衡量的是子块输出相对于“最差情况”（零输出）的改进程度。

为何选择零向量：

• 零向量作为基准是因为它代表了子块完全失效（无输出）的情况。($\text{MSE}(a_p,0)$) 提供了一个自然的参考点，用于量化子块输出的质量。相比其他可能的基准（如随机输出或平均输出），零向量更简单且计算成本低，同时与“跳过子块”（no-op操作）的场景一致。

实际意义：

• 在实践中，($\text{MSE}(a_p,0)$) 通常是一个较大的值，因为父块输出 ($a_p$) 包含有意义的特征信息。分子 ($\text{MSE}(a_p,a_c)$) 越小，说明子块越好地模仿了父块，损失值 ($\mathcal{L}$) 接近于 0。反之，如果子块输出偏离父块，($\mathcal{L}$) 会增大，但由于归一化，损失值不会因父块输出的绝对量级而失控。

---

2. 解耦BLD的原理与效率

背景：
BLD的目标是为每个变换器层构建一个子块库，包含多种注意力（attention）和前馈网络（FFN）变体的组合。每个子块通过蒸馏训练以模仿对应的父块。Puzzle提出了两种BLD策略：

• 耦合BLD：为每层训练所有可能的注意力-FFN组合。
• 解耦BLD：分别训练注意力变体（与冻结的父FFN组合）和FFN变体（与冻结的父注意力组合），然后在训练后组合成完整子块。

解耦BLD的原理：

• 在解耦BLD中，Puzzle将变换器层的子块分为两个子模块：注意力子块（(${\mathcal{A}}_i$)）和FFN子块（(${\mathcal{F}}_i$)）。对于第 (i) 层：
  1. 训练注意力变体：固定FFN子块为父模型的FFN（($f_{\text{parent}}$)），训练所有注意力变体 ( { a j } j = 1 m \{a_j\}_{j=1}^m {aj​}j=1m​)，使其与父块 ($[a_{\text{parent}},f_{\text{parent}}]$) 的输出匹配。训练的子块形式为 ($[a_j,f_{\text{parent}}]$)。
  2. 训练FFN变体：固定注意力子块为父模型的注意力（($a_{\text{parent}}$)），训练所有FFN变体 ( { f k } k = 1 n \{f_k\}_{k=1}^n {fk​}k=1n​)，使其与父块 ($[a_{\text{parent}},f_{\text{parent}}]$) 的输出匹配。训练的子块形式为 ($[a_{\text{parent}},f_k]$)。
  3. 组合子块：训练完成后，将训练好的注意力变体 ($a_j$) 和FFN变体 ($f_k$) 组合成完整子块 ($[a_j,f_k]$)，无需进一步训练。
• 这种解耦假设注意力子块和FFN子块的贡献在一定程度上是独立的，允许分别优化它们，而无需直接训练所有组合。

计算效率：

• 耦合BLD：需要训练每层的所有注意力-FFN组合。对于 ($m$) 个注意力变体、($n$) 个FFN变体和 ($l$) 个变换器层，需训练 ($m\cdot n\cdot l$) 个子块。例如，若 ($m=6$)（注意力变体）、($n=9$)（FFN变体）、($l=80$)（如Llama-3.1-70B），则需训练 ($6\cdot 9\cdot 80=4320$) 个子块。
• 解耦BLD：仅训练每层的 ($m$) 个注意力变体和 ($n$) 个FFN变体，总计 ($(m+n)\cdot l$) 个子块。以上例，需训练 ($(6+9)\cdot 80=1200$) 个子块，计算量减少约3.6倍。
• 效率提升：解耦BLD的训练量从 ($O(m\cdot n\cdot l$)) 降至 ($O((m+n)\cdot l)$)，显著降低了构建子块库的成本，尤其当 ($m$) 和 ($n$) 较大时（如 ($m=n=20$) 时，耦合需训练32000个子块，解耦仅需3200个）。

是否丢失选择空间：

• 潜在损失：解耦BLD假设注意力子块和FFN子块可以独立训练并组合，而不考虑它们在训练时的交互效应。这种假设可能导致组合后的子块 ($[a_j,f_k]$) 并非完全等价于直接训练的耦合子块，因为：
  1. 上下文依赖：注意力子块的输出会影响FFN子块的输入，解耦训练无法捕捉这种动态交互，可能导致组合子块的性能略低于耦合训练的子块。
  2. 误差累积：解耦训练的子块以父块的输出为目标，而非其他子块的输出，可能在组合后引入误差，尤其在深层模型中。
• 实际影响：
  • 论文指出，解耦BLD生成的子块库在实践中表现良好，BLD阶段已能恢复父模型的大部分性能（见表14）。这表明注意力与FFN的交互效应在蒸馏任务中可能不是主导因素。
  • Puzzle通过后续的全局知识蒸馏（GKD）阶段进一步微调整个模型，弥补了解耦带来的潜在不兼容性（如块间误差传播），确保最终模型性能接近父模型。
  • 论文还提到了一种折中方案（见Section 8.1.1），结合耦合和解耦BLD，针对关键层或组合进行耦合训练，以平衡效率和性能。
• 权衡：解耦BLD牺牲了一部分选择空间的精确性（即未直接训练某些组合的交互），但通过大幅降低计算成本，允许探索更大的搜索空间（例如更多变体或层）。这种权衡在资源受限的场景下尤为重要，且GKD阶段的校正作用进一步减轻了潜在损失。

---

3. 基于激活的通道贡献（Channel Contribution）方法

背景：
在BLD阶段，Puzzle需要初始化FFN子块的权重，特别是当FFN的中间维度被缩减（例如从100%缩减到87%、75%等）。为了加速蒸馏收敛，Puzzle提出了基于激活的通道贡献（Channel Contribution）方法，通过分析FFN中间通道的贡献来选择修剪目标。

方法原理：

• FFN结构：FFN子块通常包含上投影（up projection）、激活函数（如GeLU）和下投影（down projection）。设隐维度为 ($H$)，FFN中间维度为 ($I$)，下投影矩阵为 ($W^{\text{down}}\in {\mathbb{R}}^{I\times H}$)。对于输入 ($X\in {\mathbb{R}}^I$)（FFN中间激活），FFN输出为：

$$Y=(W^{\text{down}}{)}^{\top }X=\sum _{k=1}^I{X}_k{W}_{k,:}^{\text{down}}$$

其中 ($Y\in {\mathbb{R}}^H$) 是FFN输出，($X_k$) 是中间激活的第 ($k$) 个通道，($W_{k,:}^{\text{down}}$) 是下投影矩阵的第 ($k$) 行。

• 通道贡献定义：对于每个中间通道 ($k$)，其对FFN输出的贡献定义为移除该通道后的输出变化：

$$C_k(X)={\Vert \left(\sum _{j=1}^I{X}_j{W}_{j,:}^{\text{down}}\right)-\left(\sum _{j\ne k}{X}_j{W}_{j,:}^{\text{down}}\right)\Vert }_2=\left|X_k\right|\cdot {\Vert W_{k,:}^{\text{down}}\Vert }_2$$

其中：

• ($\left|X_k\right|$)：通道 ($k$) 的激活绝对值，反映该通道的激活强度。

• (${\Vert W_{k,:}^{\text{down}}\Vert }_2$)：下投影矩阵第 ($k$) 行的二范数，反映该通道的权重重要性。

• ($C_k(X$))：通道 ($k$) 的贡献，结合了激活强度和权重重要性。

• 计算过程：

  1. 在校准数据集（calibration dataset）上运行前向传播，收集FFN中间激活 ($X$)。
  2. 对每个通道 ($k$)，计算其贡献 ($C_k(X)$) 在数据集上的平均值，得到每个通道的平均贡献。
  3. 根据贡献从小到大排序通道，优先修剪贡献最低的通道，以初始化缩减维度的FFN子块。

方法优势：

• 数据驱动：通过校准数据集的激活值，方法捕捉了通道在实际推理中的重要性，而非仅依赖权重大小。
• 高效性：贡献计算仅需一次前向传播，计算成本低，适合大规模模型。
• 针对性：结合激活强度 ($\left|X_k\right|$) 和权重重要性 (${\Vert W_{k,:}^{\text{down}}\Vert }_2$)，确保修剪保留对输出影响最大的通道。

与传统修剪的区别：

• 传统修剪方法（如基于权重大小的L1范数修剪）仅考虑权重矩阵，忽略了输入激活的动态分布，可能错误修剪对输出贡献大的通道。
• Channel Contribution方法结合了激活和权重，类似于Wanda等基于激活的修剪技术（参考文献[40]），但专注于FFN中间通道，适用于Puzzle的蒸馏初始化场景。

实际应用：

• 在初始化缩减维度FFN时（如从100%降到50%），Puzzle根据通道贡献排序，移除低贡献通道，保留高贡献通道的权重。
• 这种初始化使子块更接近父块的输出分布，减少蒸馏训练的初始误差，加速收敛。

---

4. 总结与补充说明

• 损失函数分母：($\text{MSE}(a_p,0)$) 作为归一化因子，确保损失尺度无关且训练稳定，零向量作为基准反映了“最差输出”的场景。
• 解耦BLD：
  • 效率：通过将训练量从 ($m\cdot n\cdot l$) 降至 ($(m+n)\cdot l$)，显著降低成本。
  • 选择空间：可能丢失注意力-FFN交互的精确性，但通过GKD校正和折中方案（如部分耦合BLD）缓解影响，实践中性能接近耦合BLD。
  • 适用性：解耦BLD特别适合大规模搜索空间，允许探索更多变体。
• Channel Contribution：
  • 是一种数据驱动的初始化方法，通过激活和权重的结合评估通道重要性，优先修剪低贡献通道。
  • 相比传统修剪方法，更准确地保留对FFN输出贡献大的通道，加速蒸馏收敛。

进一步思考：

• 解耦BLD的假设（注意力与FFN独立性）可能在某些任务或模型中不完全成立，未来可通过自适应选择耦合/解耦训练的层来优化。
• Channel Contribution方法依赖校准数据集的质量，数据集的代表性可能影响修剪效果，需进一步研究其鲁棒性。

Decomposed NAS Search Algorithm for LLMs

在《PUZZLE: DISTILLATION-BASED NAS FOR INFERENCE-OPTIMIZED LLMS》论文中，Decomposed NAS Search Algorithm for LLMs（分解式神经架构搜索算法）是Puzzle框架的核心组件之一，用于在大规模语言模型（LLM）的架构空间中高效搜索推理优化的模型架构。本节将详细介绍该算法的原理、实现步骤、数学公式以及其在LLM优化中的独特贡献。内容面向深度学习研究者，深入技术细节，同时保持逻辑清晰。

---

1. 概述与背景

目标：Puzzle框架旨在通过神经架构搜索（NAS）优化LLM的推理效率（如吞吐量、延迟、内存占用），同时最大限度保留模型性能。传统NAS方法（如全模型搜索）在LLM规模（数十亿参数）下计算成本极高，且难以针对特定硬件（如NVIDIA H100 GPU）和推理场景（如FP8量化）进行优化。Puzzle提出了一种分解式NAS（Decomposed NAS），通过将搜索过程分解为块级本地蒸馏（BLD）、混合整数规划（MIP）架构搜索和全局知识蒸馏（GKD）三个阶段，显著降低搜索成本并实现硬件感知优化。

核心思想：

• 将LLM的变换器层（block）视为独立模块，分别优化每个层的注意力（attention）和前馈网络（FFN）子块。
• 使用BLD构建子块库，MIP搜索最优子块组合，GKD微调最终模型。
• 针对目标硬件的实际运行时和内存需求优化，而非仅依赖理论指标（如FLOPs）。

本节重点：分解式NAS的搜索算法（主要是MIP阶段），其数学公式、约束条件和实现细节。

---

2. 分解式NAS搜索算法的原理

分解式NAS搜索算法的核心是混合整数规划（MIP），它在BLD阶段生成的子块库中选择最优的子块组合，构建一个推理优化的LLM架构。以下是算法的整体流程和原理：

2.1 算法流程

1. 输入：

   • 子块库：BLD阶段为每个变换器层 ( i ∈ { 1 , … , l } i \in \{1, \dots, l\} i∈{1,…,l}) 生成的子块库，包含注意力子块集合 ( A i = { a i , 1 , … , a i , m } \mathcal{A}_i = \{a_{i,1}, \dots, a_{i,m}\} Ai​={ai,1​,…,ai,m​}) 和FFN子块集合 ( F i = { f i , 1 , … , f i , n } \mathcal{F}_i = \{f_{i,1}, \dots, f_{i,n}\} Fi​={fi,1​,…,fi,n​})。每层可选择 ($m\cdot n$) 种子块组合（例如，Llama-3.1-70B有80层，($m=6$)，($n=9$)，每层54种组合）。
   • 硬件约束：目标硬件（如H100 GPU）的资源限制，包括内存预算 ($M_{\text{max}}$)、延迟目标 ($L_{\text{max}}$) 或吞吐量目标。
   • 性能估计：每个子块的性能指标（通过BLD蒸馏损失估计）和硬件资源需求（通过实际测量获得，例如预填充和生成阶段的延迟）。

2. 搜索目标：

   • 最大化模型性能（通常以父模型的性能为基准，基于BLD阶段的蒸馏损失）。
   • 满足硬件约束（如内存占用、推理延迟）或优化硬件效率（如吞吐量）。

3. 输出：

   • 每层的最优子块组合 ($\{(a_{i,j},f_{i,k}){\}}_{i=1}^l$)，构成一个完整的LLM架构（如Nemotron-51B）。
   • 该架构在目标硬件上实现高吞吐量、低延迟，同时保留接近父模型的性能。

2.2 分解式NAS的关键创新

• 块级分解：将NAS问题分解为每层的子块选择，显著缩小搜索空间。传统NAS搜索整个模型架构，空间复杂度为 ($O(K^N)$)（($K$)为每层选项数，($N$)为参数规模），而分解式NAS将问题简化为 ($O(l\cdot m\cdot n)$)，其中 ($l$) 是层数（例如80）。
• 硬件感知优化：直接测量子块在目标硬件上的运行时（runtime）和内存需求，考虑批大小、序列长度和量化水平（如FP8），优于基于FLOPs的理论估计。
• 非均匀架构：允许每层选择不同的子块（如跳过注意力、缩减FFN维度），生成非均匀架构，优化资源分配。
• 高效MIP：使用MIP求解器在合理时间内找到全局最优解，避免了强化学习或进化算法的高昂成本。

---

3. 数学公式与MIP模型

MIP是分解式NAS搜索算法的核心工具，用于在子块库中选择最优组合。以下是MIP模型的详细数学公式和约束条件。

3.1 问题定义

设：

• ($l$)：变换器层数（如Llama-3.1-70B的80层）。
• ( A i = { a i , 1 , … , a i , m } \mathcal{A}_i = \{a_{i,1}, \dots, a_{i,m}\} Ai​={ai,1​,…,ai,m​})：第 ($i$) 层的注意力子块集合，包含 ($m$) 个变体（如GQA变体、线性层、no-op）。
• ( F i = { f i , 1 , … , f i , n } \mathcal{F}_i = \{f_{i,1}, \dots, f_{i,n}\} Fi​={fi,1​,…,fi,n​})：第 ($i$) 层的FFN子块集合，包含 ($n$) 个变体（如不同中间维度、线性层、no-op）。
• 每层选择一个子块组合 ($(a_{i,j},f_{i,k})$)，其中 ( j ∈ { 1 , … , m } j \in \{1, \dots, m\} j∈{1,…,m})，( k ∈ { 1 , … , n } k \in \{1, \dots, n\} k∈{1,…,n})。

目标：

• 最大化模型性能（基于BLD阶段的蒸馏损失）。
• 满足硬件约束（如内存、延迟）或优化目标（如吞吐量）。

3.2 决策变量

为每层 ($i$) 的子块组合定义二进制决策变量：
x i , j , k ∈ { 0 , 1 } , ∀ i ∈ { 1 , … , l } , j ∈ { 1 , … , m } , k ∈ { 1 , … , n } x_{i,j,k} \in \{0, 1\}, \quad \forall i \in \{1, \dots, l\}, j \in \{1, \dots, m\}, k \in \{1, \dots, n\} xi,j,k​∈{0,1},∀i∈{1,…,l},j∈{1,…,m},k∈{1,…,n}
其中：

• ($x_{i,j,k}=1$) 表示第 ($i$) 层选择注意力子块 ($a_{i,j}$) 和FFN子块 ($f_{i,k}$)。
• ($x_{i,j,k}=0$) 表示未选择该组合。

约束：每层只能选择一个子块组合：
∑ j = 1 m ∑ k = 1 n x i , j , k = 1 , ∀ i ∈ { 1 , … , l } \sum_{j=1}^m \sum_{k=1}^n x_{i,j,k} = 1, \quad \forall i \in \{1, \dots, l\} j=1∑m​k=1∑n​xi,j,k​=1,∀i∈{1,…,l}

3.3 目标函数

目标是最大化模型性能，通常通过最小化BLD阶段的累积蒸馏损失。设每个子块组合 ($(a_{i,j},f_{i,k})$) 的蒸馏损失为 (${\mathcal{L}}_{i,j,k}$)，则目标函数为：

$$\text{minimize}\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{\mathcal{L}}_{i,j,k}\cdot x_{i,j,k}$$

说明：

• (${\mathcal{L}}_{i,j,k}$) 是BLD阶段计算的归一化MSE损失，反映子块组合模仿父块的准确性（见上一节的公式 ($\mathcal{L}=\frac{\text{MSE}(a_p,a_c)}{\text{MSE}(a_p,0)}$)）。
• 最小化累积损失等价于最大化模型性能，因为较低的蒸馏损失意味着子块更接近父块的输出。

替代目标：

• 在某些场景下，Puzzle可能直接优化硬件效率（如最大化吞吐量）。例如，设每层子块组合的吞吐量为 ($T_{i,j,k}$)，目标函数可改为：
  $$\text{maximize}\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{T}_{i,j,k}\cdot x_{i,j,k}$$
• 实际中，Puzzle通常结合性能和效率，通过加权目标函数或约束条件平衡两者。

3.4 硬件约束

MIP模型通过以下约束确保架构满足硬件限制：

1. 内存约束：
   设子块组合 ($(a_{i,j},f_{i,k})$) 的内存占用为 ($M_{i,j,k}$)，总内存预算为 ($M_{\text{max}}$)，则：
   $$\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{M}_{i,j,k}\cdot x_{i,j,k}\le M_{\text{max}}$$

   • ($M_{i,j,k}$) 通过在目标硬件（如H100 GPU）上实际测量获得，考虑权重、激活、KV缓存等。

2. 延迟约束：
   设子块组合 ($(a_{i,j},f_{i,k})$) 在预填充阶段（prefill）和生成阶段（generation）的延迟分别为 ($L_{i,j,k}^{\text{prefill}}$) 和 ($L_{i,j,k}^{\text{gen}}$)，总延迟预算为 ($L_{\text{max}}$)，则：
   $$\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{L}_{i,j,k}^{\text{prefill}}\cdot x_{i,j,k}\le L_{\text{max}}^{\text{prefill}}$$
   $$\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{L}_{i,j,k}^{\text{gen}}\cdot x_{i,j,k}\le L_{\text{max}}^{\text{gen}}$$

   • 延迟测量考虑批大小、序列长度和量化水平（如FP8），反映真实推理场景。

3. 吞吐量优化（可选）：
   如果目标是最大化吞吐量，吞吐量 ($T$) 可通过延迟的倒数近似：
   $$T\propto \frac{1}{{\sum }_{i=1}^l{\sum }_{j=1}^m{\sum }_{k=1}^n{L}_{i,j,k}\cdot x_{i,j,k}}$$
   由于MIP通常处理线性目标，Puzzle可能将吞吐量目标线性化为子块的加权贡献。

3.5 完整MIP模型

综合以上，MIP模型可形式化为：

$$\text{minimize}\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{\mathcal{L}}_{i,j,k}\cdot x_{i,j,k}$$

主体约束：
∑ j = 1 m ∑ k = 1 n x i , j , k = 1 , ∀ i ∈ { 1 , … , l } \sum_{j=1}^m \sum_{k=1}^n x_{i,j,k} = 1, \quad \forall i \in \{1, \dots, l\} j=1∑m​k=1∑n​xi,j,k​=1,∀i∈{1,…,l}
$$\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{M}_{i,j,k}\cdot x_{i,j,k}\le M_{\text{max}}$$
$$\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{L}_{i,j,k}^{\text{prefill}}\cdot x_{i,j,k}\le L_{\text{max}}^{\text{prefill}}$$
$$\sum _{i=1}^l\sum _{j=1}^m\sum _{k=1}^n{L}_{i,j,k}^{\text{gen}}\cdot x_{i,j,k}\le L_{\text{max}}^{\text{gen}}$$
x i , j , k ∈ { 0 , 1 } , ∀ i , j , k x_{i,j,k} \in \{0, 1\}, \quad \forall i, j, k xi,j,k​∈{0,1},∀i,j,k

求解：

• MIP模型通过开源求解器（如Gurobi、CPLEX）或定制优化算法求解。
• 由于搜索空间仍较大（例如，80层每层54种组合，空间为 ($54^{80}\approx 10^{118}$)），Puzzle利用BLD的模块化特性，将问题分解为每层的独立选择，结合MIP的约束剪枝，显著加速求解。

---

4. 实现细节

4.1 子块库的资源测量

• 运行时测量：
  • 每个子块组合 ($(a_{i,j},f_{i,k})$) 在目标硬件上运行校准数据集，测量预填充和生成阶段的延迟（($L_{i,j,k}^{\text{prefill}}$), ($L_{i,j,k}^{\text{gen}}$)）。
  • 测量考虑实际推理引擎（如TensorKT-LLM）、批大小、序列长度和量化水平（如FP8）。
• 内存测量：
  • 计算子块的权重内存（基于参数量）、激活内存（基于批大小和序列长度）和KV缓存内存。
  • 例如，跳过注意力（no-op）的子块显著降低KV缓存需求。

4.2 性能估计

• 蒸馏损失：BLD阶段为每个子块组合计算归一化MSE损失 (${\mathcal{L}}_{i,j,k}$)，作为性能的代理指标。
• 校准数据集：使用约1B token的小数据集（如Wikipedia、Books）计算损失，无需父模型的原始训练数据。

4.3 非均匀架构支持

• Puzzle允许每层选择不同的子块，形成非均匀架构。例如：
  • 某些层跳过注意力（no-op），减少KV缓存和计算。
  • 某些层缩减FFN中间维度（如50%或25%），降低内存和延迟。
• 非均匀架构需要推理引擎支持（如TensorKT-LLM的变头数注意力支持）。

4.4 优化加速

• 约束剪枝：MIP求解器利用内存和延迟约束，快速排除不可行组合。
• 并行化：子块的资源测量和性能估计可并行执行，缩短搜索时间。
• 增量搜索：从较小模型开始（如Llama-3.1-8B），逐步扩展到大模型（如70B），复用子块库。

---

5. 算法优势与贡献

1. 高效性：

   • 分解式NAS将搜索空间从指数级降至线性级，BLD和MIP结合仅需不到50B token，远低于原始模型的15T token。
   • MIP求解器在合理时间内（数小时）找到全局最优解，优于强化学习或进化算法。

2. 硬件感知：

   • 直接优化真实硬件指标（如H100 GPU的运行时），考虑批大小、序列长度和量化，生成的架构（如Nemotron-51B）实现2.17倍吞吐量提升。

3. 灵活性：

   • 支持非均匀架构，适应多样化的硬件约束和推理场景。
   • 子块库可复用于不同任务或硬件，增强扩展性。

4. 性能保留：

   • 通过BLD和GKD，生成的模型（如Nemotron-51B）保留98.4%的父模型性能（RULER基准）。

---

6. 数学与实现的进一步说明

6.1 搜索空间规模

以Llama-3.1-70B为例：

• 80层，每层6种注意力变体（($m=6$)）和9种FFN变体（($n=9$)）。
• 每层组合数：($m\cdot n=54$)。
• 总搜索空间：($54^{80}\approx 10^{118}$)。
• 分解式NAS通过MIP约束和BLD模块化，将实际搜索复杂度降至可处理范围（每层独立选择，结合线性约束）。

6.2 权衡性能与效率

• 性能优先：最小化 ($\sum {\mathcal{L}}_{i,j,k}\cdot x_{i,j,k}$)，选择损失最低的子块。
• 效率优先：在损失约束下最大化吞吐量，例如：
  $$\text{maximize}T,\text{s.t.}\sum {\mathcal{L}}_{i,j,k}\cdot x_{i,j,k}\le {\mathcal{L}}_{\text{max}}$$
• 实际中，Puzzle可能使用多目标优化（如加权和）平衡两者。

6.3 实际案例：Nemotron-51B

• 输入模型：Llama-3.1-70B-Instruct。
• 搜索结果：Nemotron-51B，参数量缩减至51B，非均匀架构（部分层跳过注意力或缩减FFN）。
• 性能：98.4%父模型性能（RULER基准）。
• 效率：在H100 GPU上，FP8量化下吞吐量提升2.17倍，内存效率显著提高。

---

7. 未来方向

• 动态搜索：结合推理时的动态批大小和序列长度，实时调整架构。
• 多目标优化：引入Pareto前沿分析，生成多种性能-效率权衡的架构。
• 扩展性：将分解式NAS应用于其他模型（如视觉变换器）或硬件（如TPU）。
• 强化学习辅助：结合MIP和强化学习，进一步加速搜索。

---

8. 总结

分解式NAS搜索算法通过BLD、MIP和GKD三个阶段，高效地在LLM架构空间中搜索推理优化的模型。MIP模型以二进制决策变量为核心，通过最小化蒸馏损失、满足内存和延迟约束，生成如Nemotron-51B的高效非均匀架构。其硬件感知优化、模块化设计和低成本特性使其在LLM推理优化领域具有突破性意义。数学公式清晰定义了性能与效率的优化目标，实际测量确保了硬件适配性，为未来NAS研究提供了宝贵参考。

通道贡献详解

有问题：涉及到深度学习中“通道”（channel）这一术语的具体含义，以及在Puzzle框架中基于激活的通道贡献（Channel Contribution）方法中“通道”的定义和来源。以下我会详细解析“通道”在FFN（前馈网络）中的含义，为什么用“通道”这个术语，以及它在公式中的具体表示，结合FFN结构和Puzzle框架的上下文，确保清晰易懂。

---

1. 什么是“通道”？

在深度学习中，“通道”（channel）通常用来描述张量（tensor）或向量中某个特定维度上的独立成分，最初来源于卷积神经网络（CNN）中的图像处理背景。在CNN中，输入图像的每个颜色通道（如RGB的红、绿、蓝）被视为一个“通道”，扩展到卷积层中，每张特征图（feature map）也被称为一个通道。随着深度学习的普及，“通道”这一术语被泛化到其他神经网络结构中，包括变换器（Transformer）的FFN层，用来描述某些维度的独立分量。

在Puzzle框架的FFN子块中，“通道”具体指的是FFN中间激活向量 ($X\in {\mathbb{R}}^I$) 的每个标量分量（即向量 ($X$) 的每个元素 ($X_k$)，其中 ( k ∈ { 1 , … , I } k \in \{1, \dots, I\} k∈{1,…,I})）。这些分量被称为“通道”，是因为它们类似于CNN中特征图的通道，每个分量独立地通过权重矩阵（下投影矩阵 ($W^{\text{down}}$)）贡献到输出。

---

2. FFN结构与“通道”的来源

为了理解“通道”在FFN中的定义，我们先回顾FFN的结构和计算流程，然后解释为什么中间激活 ($X$) 的每个元素被称为“通道”。

2.1 FFN结构

FFN（前馈网络）是变换器层中的一个关键组件，通常由以下步骤组成：

1. 上投影（Up Projection）：将输入向量从隐维度 ($H$) 映射到更大的中间维度 ($I$)（通常 ($I\approx 4H$)）。
2. 激活函数：对中间表示应用非线性激活（如GeLU）。
3. 下投影（Down Projection）：将中间表示从维度 ($I$) 映射回隐维度 ($H$)。

数学表示如下：

• 输入：($Z\in {\mathbb{R}}^H$)（变换器层的输入，例如注意力层的输出）。
• 上投影矩阵：($W^{\text{up}}\in {\mathbb{R}}^{H\times I}$)，偏置：($b^{\text{up}}\in {\mathbb{R}}^I$)。
• 中间激活：($X=\text{GeLU}(W^{\text{up}}Z+b^{\text{up}})\in {\mathbb{R}}^I$)。
• 下投影矩阵：($W^{\text{down}}\in {\mathbb{R}}^{I\times H}$)，偏置：($b^{\text{down}}\in {\mathbb{R}}^H$)。
• 输出：($Y=(W^{\text{down}}{)}^{\top }X+b^{\text{down}}\in {\mathbb{R}}^H$)。

展开下投影的计算：
$$Y=(W^{\text{down}}{)}^{\top }X=\sum _{k=1}^I{X}_k{W}_{k,:}^{\text{down}}$$
其中：

• ($X\in {\mathbb{R}}^I$) 是中间激活向量，($X_k$) 是其第 ($k$) 个元素（标量）。
• ($W_{k,:}^{\text{down}}\in {\mathbb{R}}^H$) 是下投影矩阵 ($W^{\text{down}}$) 的第 ($k$) 行，表示第 ($k$) 个中间通道对应的权重向量。
• ($Y\in {\mathbb{R}}^H$) 是FFN的输出。

2.2 为什么 ($X_k$) 被称为“通道”？

在FFN中，中间激活向量 ($X\in {\mathbb{R}}^I$) 的每个元素 ($X_k$)（( k ∈ { 1 , … , I } k \in \{1, \dots, I\} k∈{1,…,I})）被视为一个“通道”，原因如下：

1. 独立贡献：

   • 每个 ($X_k$) 通过下投影矩阵的对应行 ($W_{k,:}^{\text{down}}$) 独立地贡献到输出 ($Y$)。具体地，输出 ($Y$) 是所有通道的加权和：
     $$Y=X_1{W}_{1,:}^{\text{down}}+X_2{W}_{2,:}^{\text{down}}+\cdots +X_I{W}_{I,:}^{\text{down}}$$
     每个 ($X_k{W}_{k,:}^{\text{down}}$) 是一个独立的分量，类似于CNN中每个特征图通道对输出的贡献。

2. 类比CNN中的通道：

   • 在CNN中，卷积层的输入是一个多通道张量（例如，($C\times H\times W$)，其中 ($C$) 是通道数）。每个通道（feature map）通过卷积核独立计算，输出是所有通道贡献的加和。
   • 在FFN中，中间激活 ($X$) 的维度 ($I$) 可以看作“通道数”，每个 ($X_k$) 类似于一个通道的激活值，通过权重 ($W_{k,:}^{\text{down}}$) 映射到输出空间。这种结构与CNN的通道处理有相似的独立性和并行性，因此借用了“通道”这一术语。

3. 语义与功能：

   • 每个 ($X_k$) 表示上投影和激活后提取的某个特征分量（feature component）。中间维度 ($I$) 通常很大（例如，Llama-3.1-70B的FFN中间维度约为28,672），每个 ($X_k$) 可以看作一个独立的“特征通道”，捕捉输入的不同方面。
   • “通道”这一术语强调了 ($X_k$) 的模块化作用：每个通道通过独立的权重向量 ($W_{k,:}^{\text{down}}$) 影响输出，类似于CNN中通道的语义。

4. 文献中的惯例：

   • 在深度学习文献中，FFN的中间维度经常被称为“通道”或“隐藏单元”（hidden units）。例如，修剪（pruning）或稀疏化（sparsification）研究（如Wanda [40]）常将FFN中间维度分解为独立通道，分析其贡献。
   • Puzzle框架沿用了这一术语，将 ($X_k$) 称为通道，以突出其在输出形成中的独立作用。

2.3 ($X_k$) 的来源

中间激活 ($X\in {\mathbb{R}}^I$) 的生成过程如下：

• 输入：变换器层输入 ($Z\in {\mathbb{R}}^H$)（例如，注意力层的输出，隐维度 ($H=7,168$) for Llama-3.1-70B）。
• 上投影：通过矩阵 ($W^{\text{up}}\in {\mathbb{R}}^{H\times I}$)，将 ($Z$) 映射到高维空间：
  $$U=W^{\text{up}}Z+b^{\text{up}}\in {\mathbb{R}}^I$$
• 激活函数：应用GeLU非线性激活，生成中间激活：
  $$X=\text{GeLU}(U)\in {\mathbb{R}}^I$$
  其中，($X_k$) 是向量 ($X$) 的第 ($k$) 个元素，代表第 ($k$) 个通道的激活值。

关键点：

• ($X_k$) 不是矩阵的行，而是向量 ($X$) 的一个标量分量（即 ($X\in {\mathbb{R}}^I$) 的第 ($k$) 个元素）。
• ($X$) 是通过上投影和GeLU激活生成的特征向量，其维度 ($I$) 表示FFN的中间表示能力。每个 ($X_k$) 是这一表示的一个“通道”，通过下投影权重 ($W_{k,:}^{\text{down}}$) 映射到输出。

---

3. 为什么不用“行”而是“通道”？

你提到“通道就是中间输入（经过上投影和激活函数）($X$) 矩阵的第 ($k$) 行吗？”——答案是不是行，而是向量 ($X$) 的第 ($k$) 个元素。以下解释为什么不用“行”而是“通道”：

1. ($X$) 不是矩阵：

   • ($X\in {\mathbb{R}}^I$) 是一个一维向量（维度为 ($I$)），而不是矩阵。因此，($X_k$) 是 ($X$) 的第 ($k$) 个标量分量，而不是矩阵的行。
   • 在FFN中，输入 ($Z$) 和输出 ($Y$) 也是向量（维度为 ($H$)），整个计算是向量到向量的映射。中间激活 ($X$) 的每个元素 ($X_k$) 是一个独立的标量，称为“通道”。

2. “行”的误解：

   • 如果将 ($X$) 视为矩阵，可能是在考虑批量输入（batch processing）场景。例如，批量输入 ($Z\in {\mathbb{R}}^{B\times H}$)（($B$) 为批大小），上投影后得到 ($U\in {\mathbb{R}}^{B\times I}$)，激活后 ($X\in {\mathbb{R}}^{B\times I}$)。在这种情况下，($X$) 的每一行对应一个样本的中间激活向量。
   • 但是，在Puzzle的Channel Contribution方法中，分析是针对单个样本的激活向量 ($X\in {\mathbb{R}}^I$) 进行的（即使在批量中，也逐样本计算通道贡献）。因此，($X_k$) 是向量 ($X$) 的第 ($k$) 个元素，而不是矩阵的行。

3. “通道”的合理性：

   • 术语“通道”强调 ($X_k$) 的独立性和功能性。每个 ($X_k$) 通过 ($W_{k,:}^{\text{down}}$) 独立影响输出 ($Y$)，类似于CNN中通道的独立贡献。
   • 使用“通道”而不是“元素”或“分量”是为了与深度学习文献保持一致，尤其是在修剪、量化或蒸馏等场景中，FFN中间维度的分量常被称为通道。

---

4. 通道贡献公式中的“通道”

现在我们回到Channel Contribution公式的上下文，重新审视“通道”的作用：

$$C_k(X)={\Vert \left(\sum _{j=1}^I{X}_j{W}_{j,:}^{\text{down}}\right)-\left(\sum _{j\ne k}{X}_j{W}_{j,:}^{\text{down}}\right)\Vert }_2=\left|X_k\right|\cdot {\Vert W_{k,:}^{\text{down}}\Vert }_2$$

• 含义：

  • ($C_k(X)$) 衡量第 ($k$) 个通道（即 ($X_k$)）对FFN输出 ($Y$) 的贡献。
  • 贡献定义为：如果移除第 ($k$) 个通道（即将 ($X_k$) 设为0），输出 ($Y$) 的变化量（用L2范数 ($\Vert \cdot {\Vert }_2$) 衡量）。
  • 推导：
    $$Y=\sum _{j=1}^I{X}_j{W}_{j,:}^{\text{down}}$$
    移除第 ($k$) 个通道后，输出变为：
    $$Y_{-k}=\sum _{j\ne k}{X}_j{W}_{j,:}^{\text{down}}$$
    变化量：
    $$Y-Y_{-k}=X_k{W}_{k,:}^{\text{down}}$$
    L2范数：
    $$C_k(X)=\Vert Y-Y_{-k}{\Vert }_2=\Vert X_k{W}_{k,:}^{\text{down}}{\Vert }_2=|X_k|\cdot \Vert W_{k,:}^{\text{down}}{\Vert }_2$$
    这里，($X_k$) 是标量，($|X_k|$) 是其绝对值；($W_{k,:}^{\text{down}}\in {\mathbb{R}}^H$) 是权重向量，($\Vert W_{k,:}^{\text{down}}{\Vert }_2$) 是其L2范数。

• “通道”的作用：

  • ($X_k$)（第 ($k$) 个通道的激活值）决定了该通道的信号强度。如果 ($X_k\approx 0$)，该通道对输出的贡献很小。
  • ($W_{k,:}^{\text{down}}$)（第 ($k$) 个通道的权重）决定了该通道的映射能力。如果 ($\Vert W_{k,:}^{\text{down}}{\Vert }_2$) 很小，说明该通道的权重不重要。
  • 贡献 ($C_k(X)$) 综合了两者：激活强度 ($|X_k|$) 和权重重要性 ($\Vert W_{k,:}^{\text{down}}{\Vert }_2$)。

• 计算过程：

  • 在校准数据集上运行前向传播，收集每个样本的中间激活 ($X$)。
  • 对每个通道 ($k$)，计算 ($C_k(X)=|X_k|\cdot \Vert W_{k,:}^{\text{down}}{\Vert }_2$)，并在数据集上取平均值，得到通道 ($k$) 的平均贡献。
  • 根据贡献排序，优先修剪低贡献通道（如在初始化缩减维度FFN时移除 ($X_k$) 和 ($W_{k,:}^{\text{down}}$)）。

---

5. 为什么称为“通道”：直观解释

为了更直观地理解为什么 ($X_k$) 被称为“通道”，可以从以下角度思考：

1. 特征提取的视角：

   • FFN的上投影和激活函数（($X=\text{GeLU}(W^{\text{up}}Z+b^{\text{up}}$)）将输入 ($Z$) 转换为高维特征表示 ($X\in {\mathbb{R}}^I$)。每个 ($X_k$) 是这一表示的一个分量，捕捉输入的某个特定模式或特征。
   • 类似于CNN中每个通道捕捉图像的某种特征（如边缘、纹理），FFN的每个 ($X_k$) 可以看作一个“特征通道”，通过 ($W_{k,:}^{\text{down}}$) 映射到输出空间。

2. 并行处理的视角：

   • FFN的中间维度 ($I$) 通常很大（例如，28,672），可以看作并行处理 ($I$) 个独立的分量。每个分量（通道）通过独立的权重向量 ($W_{k,:}^{\text{down}}$) 贡献到输出，类似于多通道并行计算。

3. 修剪的视角：

   • 在修剪或蒸馏任务中，FFN的中间维度常被分解为独立的分量，逐一分析其重要性。术语“通道”借用了CNN的语义，用来描述这些可独立修剪的分量。

---

6. 回答你的具体疑问

通道就是中间输入（经过上投影和激活函数）($X$) 矩阵的第 ($k$) 行吗？

• 答案：不是。($X\in {\mathbb{R}}^I$) 是一个向量，不是矩阵。($X_k$) 是 ($X$) 的第 ($k$) 个元素（标量），而不是矩阵的行。
• 如果考虑批量输入，($X\in {\mathbb{R}}^{B\times I}$)（($B$) 为批大小），每一行是单个样本的激活向量。但在Channel Contribution方法中，分析是针对单个样本的 ($X\in {\mathbb{R}}^I$)，因此 ($X_k$) 是向量的第 ($k$) 个分量。

为什么它称为通道呢？这是如何来的？

• 答案：
  • “通道”是指 ($X_k$)，即中间激活向量 ($X\in {\mathbb{R}}^I$) 的第 ($k$) 个元素。称为“通道”是因为：
    1. 每个 ($X_k$) 独立地通过权重 ($W_{k,:}^{\text{down}}$) 贡献到输出，类似于CNN中通道的独立性。
    2. 术语“通道”借用了CNN的语义，泛化到FFN的中间维度，表示可独立分析的特征分量。
    3. 文献惯例（如Wanda等修剪方法）将FFN中间维度的分量称为通道，Puzzle沿用了这一术语。
  • 来源：($X_k$) 来自FFN的上投影和激活：
    $$X=\text{GeLU}(W^{\text{up}}Z+b^{\text{up}})$$
    其中 ($X_k$) 是 ($X$) 的第 ($k$) 个元素，代表第 ($k$) 个通道的激活值。

---

7. 总结

• 通道的定义：在Puzzle的FFN中，“通道”是指中间激活向量 ($X\in {\mathbb{R}}^I$) 的每个元素 ($X_k$)（标量），而不是矩阵的行。每个 ($X_k$) 通过下投影权重 ($W_{k,:}^{\text{down}}$) 独立贡献到输出 ($Y$)。
• 为什么叫通道：
  • ($X_k$) 的独立性和并行性类似于CNN中的特征通道。
  • 术语“通道”借用了CNN的语义，泛化到FFN的中间维度，符合深度学习文献惯例。
  • 每个 ($X_k$) 代表一个特征分量，通过权重映射到输出，适合称为“通道”。
• 来源：($X_k$) 是FFN上投影（($W^{\text{up}}Z+b^{\text{up}}$)）和GeLU激活后生成的中间激活 ($X$) 的第 ($k$) 个元素。
• 在Channel Contribution中的作用：通道贡献 ($C_k(X)=|X_k|\cdot \Vert W_{k,:}^{\text{down}}{\Vert }_2$) 衡量第 ($k$) 个通道对输出的重要性，用于初始化缩减维度的FFN子块。

后记

2025年5月8日于上海，在grok 3大模型辅助下完成。