【数据挖掘】基于密度的聚类方法 - OPTICS 方法 ( 核心距离 | 可达距离 | 族序 )

I . 核心距离 概念

---

1 . 核心距离概念引入 : 必须是核心对象 , 才有核心距离 ;

2 . 已知条件 :

① 数据集合 : 给定 数据集 $D$ ;

② 参数 : 给定两个参数 , $\epsilon$-邻域半径参数 $\epsilon$ , MinPts 参数 ( $\epsilon$-邻域中样本个数最小阈值 ) ;

③ 数据样对象 : 给定一个数据样本 $O$ ;

3 . 样本 $O$ 是核心对象 : 此类情况 核心距离有意义 , 如果是边界对象无意义 ;

① 核心距离概念引入 : 如果该样本对象 $O$ 是核心对象 , 那么 $O$ 对象的 核心距离 , 就是使样本 $O$ 能够成为 核心对象 的 最小半径值 $\epsilon$ 参数 ;

② 核心距离要求 ( 恰好核心的最小距离 ) : 是使得 $O$ 能成为 核心对象 的 最小距离 , 不是 之前设定的 $\epsilon$ 参数 , 该核心距离小于等于 $\epsilon$ 参数 , 样本 $O$ 的 $\epsilon$-邻域 内可能有多于 MinPts 个样本 , 但是我们只取其半径范围内 恰好 有 MinPts 样本的 半径值 $\epsilon$ 作为其核心距离 ;

③ 核心距离种类个数 : 不同的样本 , 核心距离可能不同 , $10$ 个样本 , 可能有 $10$ 个核心距离 ;

④ 样本 $O$ 是核心对象判定条件 : 以样本 $O$ 为中心点 , 再其 $\epsilon$ 半径区域范围内 ( $\epsilon$-邻域 ) , 样本个数多于 MinPts 最小阈值 ;

4 . 样本 $O$ 不是核心对象 : 如果该样本对象 $O$ 不是核心对象 , 是 边界对象 , 那么 该样本的 核心距离 概念没有意义 ;

II . 核心距离值

---

核心距离确定 :

① 样本 $O$ 是 边界对象 : 核心距离 无穷大 ; 样本 $O$ 的 $\epsilon$-邻域 的样本个数小于 MinPts 个 ;

② 样本 $O$ 是 核心对象 : 核心距离 是保证 半径范围内恰好有 MinPts 个样本的最小半径 , 一定要注意 , 就是 卡着第 MinPts 个样本点的圆的半径 , 从 $O$ 核心对象到第 MinPts 个样本的距离 / 半径 ;

III . 核心距离 示例

---

1 . 已知条件 :

① $\epsilon$-邻域 半径参数 : $\epsilon$ ;

② MinPts 阈值参数 : MinPts $=5$ , $\epsilon$-邻域中样本个数最小阈值 , 达到该阈值 , 样本才能算作核心对象 ;

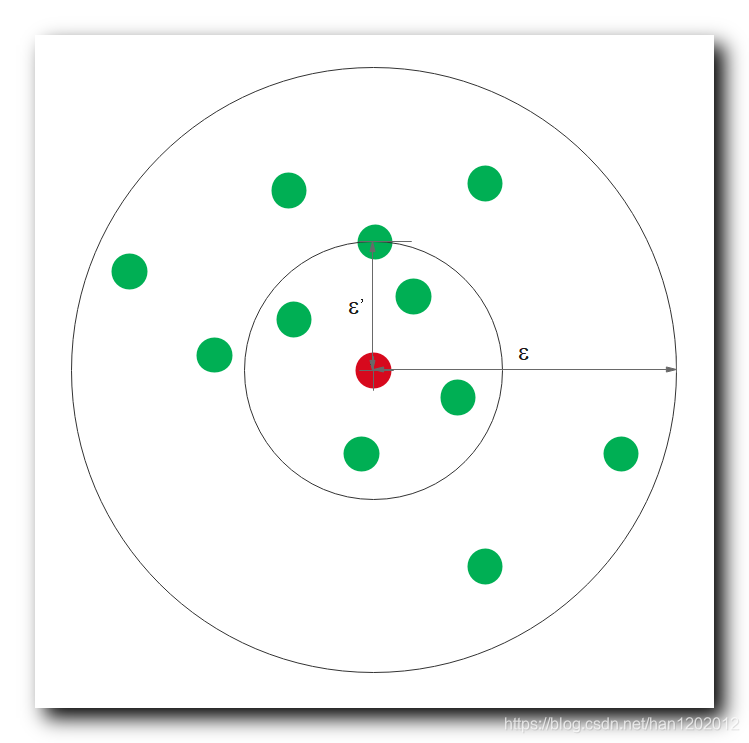
③ 核心对象 : 红色点是 核心对象 ;

④ $\epsilon$-邻域 : 外层的圆 , 以核心对象 ( 红色样本 ) 为中心 , $\epsilon$ 参数为半径 , 的区域范围 , 是 $\epsilon$-邻域 ;

2 . 核心距离分析 :

① 核心距离要求 : 样本的 核心距离 是保证 半径范围内恰好有 MinPts 个样本的最小半径 ;

② $\epsilon$ 半径说明 : 这里 $\epsilon$ 半径内有 $11$ 个样本 , 这个 $\epsilon$ 不是我们要的核心距离 ;

③ 本案例的核心距离 : 要恰好保证有 核心距离半径范围内 MinPts $=5$ 样本 , 的最小半径值 ;

④ 注意两点 : 第一 , 恰好保证区域内有 $5$ 个样本 ; 第二 , 最小半径 ;

⑤ 核心距离确定 : 这两个条件唯一确定了一个半径值 ${\epsilon }^{\prime }$ ;

IV . 可达距离

---

1 . 可达距离概念引入 : 必须是核心对象 , 才有可达距离 ;

2 . 已知条件 :

① 数据集合 : 给定 数据集 $D$ ;

② 参数 : 给定两个参数 , $\epsilon$-邻域半径参数 $\epsilon$ , MinPts 参数 ( $\epsilon$-邻域中样本个数最小阈值 ) ;

③ 数据样对象 : 给定一个数据样本 $O$ ;

3 . 样本 $O$ 是核心对象 : 此类情况 可达距离有意义 , 如果是边界对象 可达距离 无意义 ;

4 . 可达距离概念 :

① 前提 : 样本 $O$ 必须是核心对象 ;

② 核心距离 : 样本 $O$ 的核心距离 ;

③ 欧几里得距离 : $O$ 和 $p$ 之间的 欧几里得距离 , 这里与 曼哈顿距离 对照 ;

④ 可达距离 : 样本 $O$ 与样本 $p$ 之间的可达距离是 , 核心距离 与 欧几里得距离 的 较大的值 ;

V . 可达距离 示例

---

1 . 已知条件 :

① $\epsilon$-邻域 半径参数 : $\epsilon$ ;

② MinPts 阈值参数 : MinPts $=5$ , $\epsilon$-邻域中样本个数最小阈值 , 达到该阈值 , 样本才能算作核心对象 ;

③ 样本 $O$ : 是核心对象 , 中心的红点 ;

④ $\epsilon$-邻域 : 外层的圆 , 以核心对象 ( 红色样本 ) 为中心 , $\epsilon$ 参数为半径 , 的区域范围 , 是 $\epsilon$-邻域 ;

⑤ 样本 $p_1$ : 在 样本 $O$ 核心距离范围内 ;

⑥ 样本 $p_2$ : 在样本 $O$ 核心距离范围外 , 在 $\epsilon$ 半径之内 ;

2 . 可达距离 :

① 样本 $O$ 与 样本 $p_1$ 的可达距离 : 在 核心距离 ${\epsilon }^{\prime }$ 与 $O$ 与 $p_1$ 欧几里得距离 选较大的那个 , 选择 核心距离 ;

② 样本 $O$ 与 样本 $p_2$ 的可达距离 : 在 核心距离 ${\epsilon }^{\prime }$ 与 $O$ 与 $p_2$ 欧几里得距离 选较大的那个 , 选择 欧几里得距离 ;

VI . 可达距离 总结

---

可达距离总结 :

① 核心距离内 : 样本 $O$ 与其核心距离内的样本的可达距离 都是 核心距离 值 ;

② 核心距离外 ( $\epsilon$-邻域内 ) : 样本 $O$ 与其核心距离外的样本的可达距离 都是 样本 $O$ 与其它样本的 欧几里得距离 ;

VII . 族序 ( Cluster Ordering ) 概念

---

1 . 族序 ( Cluster Ordering ) 概念 :

① 多层次同时聚类 : 不同层次的聚类分组 , 可以同时进行构建 ;

② 顺序处理样本 : 处理数据集样本对象时 , 使用特定的顺序进行处理 ;

③ 顺序扩展 : 数据集样本对外扩展时 , 按照该顺序进行扩展 ,

④ 族序概念 : 该特定顺序就是 族序 ( Cluster Ordering ) ;

2 . 聚类顺序 : 从 低层 到 高层 ; 从 稠密 到 稀疏 ;

聚类时 , 低层 的聚类分组 要首先构建完成 , 也就是 $\epsilon$ 参数 较小的聚类分组 ;

3 . 密度可达的两种情况情况 : 两个样本 密度可达 , 有两种情况 :

① $\epsilon$ 参数小 : 一种情况是 $\epsilon$ 参数 较小的时候 , 这两个样本就可以密度可达 ;

② $\epsilon$ 参数大 : 另一种情况是 $\epsilon$ 参数 取值很大时 , 才可以密度可达 ;

4 . 扩展样本优先级 : 扩展样本对象时 , 优先选择第一种情况 , $\epsilon$ 参数 较小的时候 就可以密度可达的样本 ;

5 . 每个样本对象需要存储两个值 : 核心距离 与 可达距离 ;