【运筹学】线性规划数学模型 ( 求解基矩阵示例 | 矩阵的可逆性 | 线性规划表示为 基矩阵 基向量 非基矩阵 非基向量 形式 )

一、求解基矩阵示例

---

求如下线性规划的基矩阵 :

$$\begin{array}{l}maxZ=4x_1-2x_2-x_3\\ \\ \{\begin{array}{ll}5x_1+x_2-x_3+x_4=3& \\ & \\ -10x_1+6x_2+2x_3+x_5=2& \\ & \\ x_j\ge 0& (i=1,2,3,4,5)\end{array}\end{array}$$

求解过程 :

系数矩阵 : 上述线性规划的约束方程的系数矩阵为 $\left[\begin{array}{ccccccc}& 5& 1& -1& 1& 0& \\ & & & & & & \\ & -10& 6& 2& 0& 1& \end{array}\right]$ , 这是一个 $2\times 5$ 矩阵 , $2$ 行 , $5$ 列 , 有 $2$ 个约束方程 , $5$ 个变量 ;

其 $2$ 阶的子矩阵有 $C(5,2)$ 个 , 这是组合计算公式 ; 单纯的从 $5$ 个向量中选出 $2$ 个向量 , 不用进行排列 ;

$$\begin{array}{lcl}C(5,2)& =& \frac{P(5,2)}{2!}\\ & & \\ & =& \frac{5!}{3!\times 2!}\\ & & \\ & =& \frac{5\times 4\times 3\times 2\times 1}{3\times 2\times 2}\\ & & \\ & =& 10\end{array}$$

从上述 10 个 $2$ 阶方阵中 , 将基矩阵挑选出来 ;

基矩阵的条件 : 矩阵是可逆的 ;

其中有一个子矩阵 $\left[\begin{array}{cccc}& 5& -1& \\ & & & \\ & -10& 2& \end{array}\right]$ 该矩阵是成比例的 , 不是基矩阵 ;

$10$ 个 $2$ 阶子矩阵中 , 有 $1$ 个不是可逆矩阵 , 其余 $9$ 个都是可逆矩阵 , 因此下面的 $9$ 个矩阵是基矩阵 :

$B_1=\left[\begin{array}{cccc}& 5& 1& \\ & & & \\ & -10& 6& \end{array}\right]$ , $B_2=\left[\begin{array}{cccc}& 1& -1& \\ & & & \\ & 6& 2& \end{array}\right]$ , $B_3=\left[\begin{array}{cccc}& 5& 0& \\ & & & \\ & -10& 1& \end{array}\right]$ ,

$B_4=\left[\begin{array}{cccc}& 1& 1& \\ & & & \\ & 6& 0& \end{array}\right]$ , $B_5=\left[\begin{array}{cccc}& 5& 1& \\ & & & \\ & -10& 0& \end{array}\right]$ , $B_6=\left[\begin{array}{cccc}& -1& 0& \\ & & & \\ & 2& 1& \end{array}\right]$ ,

$B_7=\left[\begin{array}{cccc}& -1& 1& \\ & & & \\ & 2& 0& \end{array}\right]$ , $B_8=\left[\begin{array}{cccc}& 1& 10& \\ & & & \\ & 6& 1& \end{array}\right]$ , $B_9=\left[\begin{array}{cccc}& 1& 0& \\ & & & \\ & 0& 1& \end{array}\right]$ ;

二、矩阵的可逆性分析

---

矩阵的可逆性分析 :

矩阵可逆 :

• 可逆前提 : 分析矩阵是否可逆 , 前提是该矩阵是一个方阵 ;
• 行列式为 $0$ : 求方阵 $B$ 的行列式 , 只要该行列式不为 $0$ , 该矩阵就是可逆的 ;

行列式计算 : 使用对角线法 , 或行列余子式进行计算 , 参考以下链接 :

• n阶行列式的计算方法
• 三阶行列式

$2$ 阶方阵行列计算方法 : 本篇博客中涉及到 $2$ 阶方阵的行列式 , 其行列式就是对角线乘积相减 ;

如上述矩阵 $\left[\begin{array}{cccc}& 5& -1& \\ & & & \\ & -10& 2& \end{array}\right]$ , 其对角线乘积相减 :

$$\begin{array}{lcl}D& =& \left|\begin{array}{cc}5& -1\\ -10& 2\end{array}\right|\\ & & \\ & =& (5\times 2)-(-1\times -10)\\ & & \\ & =& =10-10\\ & & \\ & =& 0\end{array}$$

该矩阵行列式计算结果为 $0$ , 不是可逆矩阵 ;

可逆矩阵都可以写成阶梯型矩阵 ; 进行矩阵变换后 , 就可以变成阶梯矩阵 ;

三、基矩阵、基向量、基变量

---

上述 $9$ 个矩阵都是可逆矩阵 , 都可以作为基矩阵 , 当选中一个基矩阵时 , 其对应的列向量就是基向量 , 对应的变量 , 就是基变量 , 剩余的变量是非基变量 ;

选中 $B_1=\left[\begin{array}{cccc}& 5& 1& \\ & & & \\ & -10& 6& \end{array}\right]$ 作为线性规划的基矩阵 , 该基矩阵对应的基向量是 $\left[\begin{array}{ccc}& 5& \\ & & \\ & -10& \end{array}\right]$ 和 $\left[\begin{array}{ccc}& 1& \\ & & \\ & 6& \end{array}\right]$ , 对应的基变量是 $x_1$ 和 $x_2$ , $x_3,x_4,x_5$ 是非基变量 ;

选中 $B_9=\left[\begin{array}{cccc}& 1& 0& \\ & & & \\ & 0& 1& \end{array}\right]$ 作为线性规划的基矩阵 , 该基矩阵对应的基向量是 $\left[\begin{array}{ccc}& 1& \\ & & \\ & 0& \end{array}\right]$ 和 $\left[\begin{array}{ccc}& 0& \\ & & \\ & 1& \end{array}\right]$ , 对应的基变量是 $x_4$ 和 $x_5$ , $x_1,x_2,x_3$ 是非基变量 ;

基是不唯一的 , 基向量不是固定的 , 基变量也不是固定的 , 非基变量也不是固定的 ;

确定基矩阵后 , 才能确定基向量 , 基变量 , 非基变量 ;

不管选哪个矩阵作为基矩阵 , 基变量的个数是不变的 , 始终是 $2$ 个 ;

基变量不固定 , 基变量的个数是固定的 ;

基变量是 $2$ 个 , 非基变量是 $3$ 个 , 这是确定的 ;

线性规划的最终目的是求解 ; 求可行解 , 求最优解 ;

求解就是求 线性规划标准形式 , 约束条件等式的方程组的解 , 只要是等式 , 就可以解除满足条件的解 ;

解方程组的方法就是高斯消元法 , 将系数矩阵变成阶梯形的矩阵 , 只有矩阵是可逆矩阵的情况下 , 才能变成阶梯矩阵 , 就是上述的基矩阵 ;

四、线性规划等式变型

---

解如下方程 :

$$AX=b$$

其中 $A$ 是 $m\times n$ 矩阵 , $X$ 是 $m\times 1$ 向量 , $b$ 是 $m\times 1$ 向量 ;

如下展开为 :

$$(P_1{P}_2\cdots P_m{P}_{m+1}\cdots P_n)\times \left(\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_m\\ x_{m+1}\\ ⋮\\ x_n\end{array}\right)=b$$

$A$ 矩阵是由一系列向量组成 , 其一定有可逆的子矩阵 , 即基矩阵 ;

假设前 $m$ 个向量组成的矩阵是可逆矩阵 ,

前 $m$ 个列向量构成可逆矩阵 $B$ , 可逆矩阵 $B$ 中的列向量对应的变量是 $m$ 个基变量 $X_B$ ;

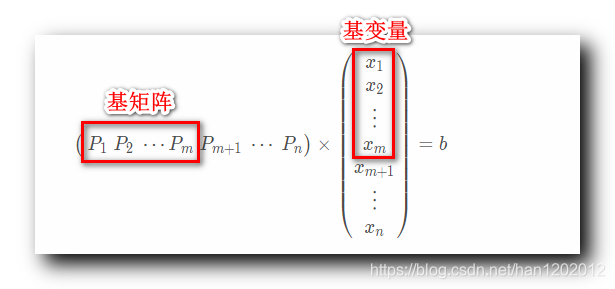
后面的 $n-m$ 个列向量后构成矩阵 $N$ , 这是非基矩阵 , 其对应的 $n-m$ 个变量是非基变量 $X_N$ ;

整个线性规划表示为 : $$B{X}_B+N{X}_N=b$$