Kalman滤波器的C++实现

Alexon Xu

已于 2023-09-02 23:30:17 修改

阅读量1.8w

点赞数 47

分类专栏：卡尔曼滤波文章标签：卡尔曼滤波 C++ python

于 2018-08-16 21:22:02 首次发布

本文链接：https://blog.csdn.net/shuoyueqishilove/article/details/81713142

版权

卡尔曼滤波专栏收录该内容

1 篇文章

订阅专栏

1、原理介绍

kalman滤波在状态估计和多传感器融合等方面应用广泛，典型的应用有无人机的飞行姿态估计，汽车的行驶状态估计，无人驾驶中的激光雷达和其他传感器之间的融合等。至于Kalman滤波的数学推导，比较复杂，需要数学功底比较好，我看了很多次书还是不会推导，放弃了，拿过来用就行了。有点儿拿来主义了。还是的介绍下kalman滤波所涉及的系统微分方程和几个核心公式。kalman滤波分为预测和更新两步。

1）线性系统微分表达

根据现代控制理论，一个线性系统可以被描述为以下形式：
状态方程：
$x_k=Ax_{k-1}+Bu_k+w_k$
观测方程：
$z_k=Hx_k+v_k$
这是空间状态表达式，现代控制理论里有。 $w_k$ 是过程噪声，服从高斯分布， $v_k$ 是观测噪声，也服从高斯分布，即：
$p (w) - N (0, Q)$
$p (v) - N (0, R)$
其中Q是过程噪声的协方差，R是观测噪声的协方差。
kalman滤波分为预测和更新两步。

2）预测

预测是根据上一时刻的状态量，由系统的微分方程预测下一时刻的系统状态量，并且产生状态量误差协方差的先验估计矩阵P
状态预测：
$KaTeX parse error: Expected 'EOF', got '̂' at position 3: x ̲̂_k^-=Ax ̂_{k-1}…$
误差协方差矩阵预测：
$P_k^-=AP_{k-1} A^T+Q$

3)更新

状态更新首先根据前面预测的状态量x由观测方程计算出理论上的观测值，然后获得传感器的实际测量值，将这两个值做差，计算出kalman滤波器的增益K，进而校正之前的预测值。同时需要计算后验的误差协方差矩阵P：
增益矩阵：
$K_k={P_k^- }{H^T}/{( H{P_k^-} H^T+R)}$
状态更新：
$KaTeX parse error: Expected 'EOF', got '̂' at position 3: x ̲̂_k=x ̂_k^-+K_k \dots$
误差协方差矩阵更新：
$P_k=(I-K_k H) P_k^-$
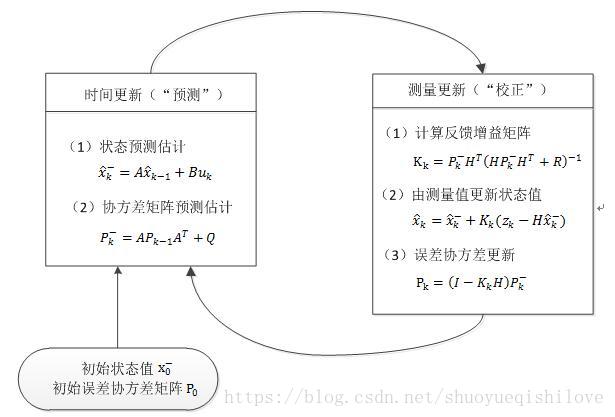
其实Kalman用起来一点儿也不复杂，最主要的是要找到系统的微分方程。然后套用上面的五个核心公式即可。典型的kalman滤波流程如下图所示：
这里写图片描述

2、C++实现kalman滤波

针对kalman滤波的流程，开发一个KalmanFilter类，专门用于实现经典kalman滤波，注意：经典Kalman滤波智能用于线性系统的滤波，即系统的状态方程和观测方程都是线性的。
由于Kalman滤波需要大量使用矩阵运算，这里使用开源矩阵运算库Eigen,关于这个库的使用。可以参考这个博客：
[https://blog.csdn.net/liufengl138/article/details/78405652]
给出实现kalman滤波类的头文件和具体实现，类定义：

#ifndef _MYKALMAN_H
#define _MYKALMAN_H
#include <Eigen\Dense>


class KalmanFilter
{
private:
	int stateSize; //state variable's dimenssion
	int measSize; //measurement variable's dimession
	int uSize; //control variables's dimenssion
	Eigen::VectorXd x;
	Eigen::VectorXd z;
	Eigen::MatrixXd A;
	Eigen::MatrixXd B;
	Eigen::VectorXd u;
	Eigen::MatrixXd P;//coveriance
	Eigen::MatrixXd H;
	Eigen::MatrixXd R;//measurement noise covariance
	Eigen::MatrixXd Q;//process noise covariance
public:
	KalmanFilter(int stateSize_, int measSize_,int uSize_);
	~KalmanFilter(){}
	void init(Eigen::VectorXd &x_, Eigen::MatrixXd& P_,Eigen::MatrixXd& R_, Eigen::MatrixXd& Q_);
	Eigen::VectorXd predict(Eigen::MatrixXd& A_);
	Eigen::VectorXd predict(Eigen::MatrixXd& A_, Eigen::MatrixXd &B_, Eigen::VectorXd &u_);
	void update(Eigen::MatrixXd& H_,Eigen::VectorXd z_meas);
};

实现：

KalmanFilter::KalmanFilter(int stateSize_ = 0, int measSize_ = 0, int uSize_=0) :stateSize(stateSize_), measSize(measSize_), uSize(uSize_)
{
	if (stateSize == 0 || measSize == 0)
	{
		std::cerr << "Error, State size and measurement size must bigger than 0\n";
	}

	x.resize(stateSize);
	x.setZero();

	A.resize(stateSize, stateSize);
	A.setIdentity();

	u.resize(uSize);
	u.transpose();
	u.setZero();

	B.resize(stateSize, uSize);
	B.setZero();

	P.resize(stateSize, stateSize);
	P.setIdentity();

	H.resize(measSize, stateSize);
	H.setZero();

	z.resize(measSize);
	z.setZero();

	Q.resize(stateSize, stateSize);
	Q.setZero();

	R.resize(measSize, measSize);
	R.setZero();
}

void KalmanFilter::init(Eigen::VectorXd &x_, Eigen::MatrixXd& P_, Eigen::MatrixXd& R_, Eigen::MatrixXd& Q_)
{
	x = x_;
	P = P_;
	R = R_;
	Q = Q_;
}
Eigen::VectorXd KalmanFilter::predict(Eigen::MatrixXd& A_, Eigen::MatrixXd &B_, Eigen::VectorXd &u_)
{
	A = A_;
	B = B_;
	u = u_;
	x = A*x + B*u;
	Eigen::MatrixXd A_T = A.transpose();
	P = A*P*A_T + Q;
	return x;
}

Eigen::VectorXd KalmanFilter::predict(Eigen::MatrixXd& A_)
{
	A = A_;
	x = A*x;
	Eigen::MatrixXd A_T = A.transpose();
	P = A*P*A_T + Q; 
//	cout << "P-=" << P<< endl;
	return x;
}

void KalmanFilter::update(Eigen::MatrixXd& H_,Eigen::VectorXd z_meas)
{
	H = H_;
	Eigen::MatrixXd temp1, temp2,Ht;
	Ht = H.transpose();
	temp1 = H*P*Ht + R;
	temp2 = temp1.inverse();//(H*P*H'+R)^(-1)
	Eigen::MatrixXd K = P*Ht*temp2;
	z = H*x;
	x = x + K*(z_meas-z);
	Eigen::MatrixXd I = Eigen::MatrixXd::Identity(stateSize, stateSize);
	P = (I - K*H)*P;
//	cout << "P=" << P << endl;
}

在类KalmanFilter的构造函数中主要根据状态变量数目、观测变量数目、控制变量数目等实现对所有涉及到的矩阵和向量的初始化，这里的初始化是粗糙的，后面接着调用init()方法实现对矩阵P，Q，R和初始状态变量的精确初始化，这个在实际中通常是通过第一次测量值来初始化初始状态。在预测函数predict()中通过输入实时的状态转移矩阵实现对状态变量和误差协方差矩阵的先验估计。然后通过传感器测量一次观测变量，进行更新过程，update()函数输入实时观测H和传感器测量值z_meas实现对预测的校正。在系统运行期间，预测和更新两个过程交替进行，实现对系统状态的实时估计。

3、实例验证

验证的情景假设为雷达追踪目标的情景，系统的状态方程为
$\left[ \begin{matrix} x \\ y \\ Vx\\ Vy\\ ax \\ ay \\ \end{matrix} \right] _{k+1}= \left[ \begin{matrix} 1 & 0 & \delta_t & 0 &0.5\delta_t^2 &0\\ 0 & 1 & 0 & \delta_t & 0&0.5\delta_t^2 \\ 0 & 0 & 1& 0 & \delta_t & 0 \\ 1 & 0 & 0 & 1& 0 & \delta_t \\ 0 & 0 & 0 & 0& 1 &0 \\ 0 & 0 & 0 & 1& 0 &1 \\ \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ Vx\\ Vy\\ ax\\ ay \end{matrix} \right]_{k}$
观测方程为：
$\left[ \begin{matrix} x \\ y \\ \end{matrix} \right] _{k+1}= \left[ \begin{matrix} 1 &0 &0 &0 &0 &0\\ 0 &1 &0 &0 &0 &0\\ \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ Vx\\ Vy\\ ax\\ ay \end{matrix} \right]_k$
测试代码如下：

#include <iostream>
#include "Eigen\Dense"
#include "myKalman.h"
#include <fstream>

using namespace std;
#define N 1000
#define T 0.01

double func(double& x);
double data_x[N],data_y[N];

double func(double& x)
{
	double res = 5*x*x;
	return res;
}

float sample(float x0, float v0, float acc, float t)
{
	return x0 + v0*t + 1 / 2 * acc*t*t;
}

float GetRand()
{
	return 0.5 * rand() / RAND_MAX - 0.25;
}

int main()
{
	ofstream fout;
	fout.open("data.txt");
	float t;
	for (int i = 0; i < N; i++)
	{
		/*data_x[i] = i*T*10;
		data_y[i] = func(data_x[i]);*/
		t = i*T;
		data_x[i] = sample(0, -4, 0, t) + GetRand();
		data_y[i] = sample(0, 6.5, 0, t) + GetRand();
	}
	int stateSize = 6;
	int measSize = 2;
	int controlSize = 0;
	KalmanFilter kf(stateSize, measSize, controlSize);
	Eigen::MatrixXd A(stateSize, stateSize);
	A << 1, 0, T, 0, 1 / 2 * T*T, 0,
		0, 1, 0, T, 0, 1 / 2 * T*T,
		0, 0, 1, 0, T, 0, 
		0, 0, 0, 1, 0, T,
		0, 0, 0, 0, 1, 0,
		0, 0, 0, 0, 0, 1;
	//cout << A;
	Eigen::MatrixXd B(0,0);
	Eigen::MatrixXd H(measSize, stateSize);
	H << 1, 0, 0, 0, 0, 0,
		0, 1, 0, 0, 0, 0;
	//cout << H;
	Eigen::MatrixXd P(stateSize, stateSize);
	P.setIdentity();
	Eigen::MatrixXd R(measSize, measSize);
	R.setIdentity()*0.01;
	Eigen::MatrixXd Q(stateSize, stateSize);
	Q.setIdentity()*0.001;
	Eigen::VectorXd x(stateSize);
	Eigen::VectorXd u(0);
	Eigen::VectorXd z(measSize);
	z.setZero();
	Eigen::VectorXd res(stateSize);

	for (int i = 0; i < N; i++)
	{
		//cout << "state_" << i << ":\n";
		if (i == 0)
		{
			x << data_x[i], data_y[i], 0, 0, 0, 0;
			kf.init(x, P, R, Q);
		}
		res<< kf.predict(A);
		z << data_x[i], data_y[i];
		kf.update(H,z);
		fout << data_x[i] << " " << res[0] << " " << data_y[i] << " " << res[1] << " " << res[2] << " " << res[3] << " " << res[4] << " " << res[5] << endl;
	}
	fout.close();
	cout << "Done, use python script to draw the figure....\n";
	system("pause");
	return 0;
}