最优化学习笔记2（交替方向法、单纯形法）

之前介绍的牛顿法、拟牛顿法、最速下降法、共轭方向法都需要知道最优化目标函数的梯度，但是在现实情况下，目标函数的梯度不方便求解甚至目标函数本身未知，此时再用无约束非线性规划的导数方法不现实，于是就有了无约束非线性规划的直接方法。

1.交替方向法（坐标循环法、Hooke&Jeeves Method、Rosenbrock）

1.1坐标循环法

不计算目标函数的梯度，在坐标轴方向上循环搜索。包含在HJ方法的第一部分。

1.2Hooke&Jeeves Method

不计算目标函数的梯度，在坐标轴方向上循环搜索。包含两个部分：探测搜索和模式搜索。

探测搜索：先以基本步长lameda作为探测步长，在正和负两个方向上分别探测。若函数值在某一个方向上有下降，则增加探测步长，继续在该方向上探测，直到函数值不再下降为止，以最终的探测步长作为结果。若函数值在两个方向上的探测均无下降，则减小探测步长，重复两个方向的探测过程。若探测步长减小到一个容许值还未使函数值有任何下降，则保持当前探测点不变，即最终探测步长为 0.

模式搜索：以基本步长lameda在方向d上进行探测，若目标函数值有下降，则增加步长再探测，直到不能再下降为止。若无下降，则减少步长再探测。若步长已经减小到容许值目标函数仍无任何下降，则模式搜索失败，返回步长 入=o作为结果。

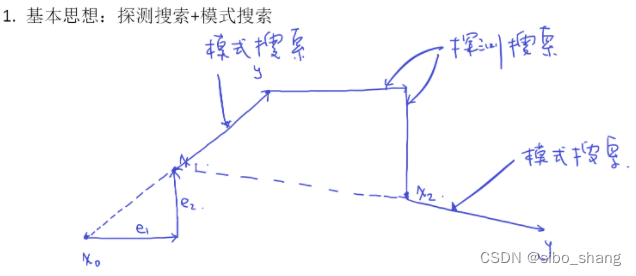
简单来说，就是先试再猜，第一步先在各个方向上探索一遍，第二部再根据经验试一试。

下面是代码的过程，循环里面的上半部分是探测搜索（坐标循环法），下半部分是模式搜索，一共要探测255次，我补上了模式搜索，迭代步骤只需要八步，还是很有效果的。

% Cyclic coordinate method for minimizing a function of several variables
% without using any derivative information.
% x0 is a row vector.

function [xmin,fmin]=Cyclic_Coordinate_Method(x0)

epsilon=1e-5;
x_k=x0;
n=length(x0);
D=eye(n);
k=0;

while 1
    % coordinate search 这里使用探测搜索
    y_j=x_k;
    for j=1:n
        d_j=D(:,j);
        lambda_j=fminbnd(@(lambda) theta(lambda,y_j,d_j),-10,10);
        y_j=y_j+lambda_j*d_j;
    end
    x_kplus1=y_j;
    
    % stop criteria
    if (norm(x_kplus1-x_k)<epsilon) && (objective_fun(x_k)-objective_fun(x_kplus1)<epsilon)
        xmin=x_kplus1;
        fmin=objective_fun(xmin);
        k
        return;
    end
    
    % iteration
    %这里使用模式搜索
    d_k=x_kplus1-x_k;
    lambda_j=fminbnd(@(lambda) theta(lambda,y_j,d_k),0,10);
    x_kplus1=x_kplus1+lambda_j*d_k;

    x_k=x_kplus1;
    k=k+1;
end

原函数如下：

function y=objective_fun(x)

y=(x(1)-2)^4+(x(1)-2*x(2))^2;

计算函数值函数如下：

function y=theta(lambda,y_j,d_j)

x=y_j+lambda*d_j;
y=objective_fun(x);

测试函数如下：

clear;
clc;
x0=[100;1];
[xmin,fmin]=Cyclic_Coordinate_Method(x0);
xmin
fmin

1.3 Rosenbrock method

类似的，Rosenbrock 方法包括探测搜索和构造搜索方向两个部分，探测搜索沿n个单位正交的方向进行。探测搜索结束后，在新的迭代点处重新构造n个正交的方向以备进行下一次探测搜索。

在构造搜索方向时涉及到施密特正交化

代码如下：

%Method of Rosenbriock using line searches

function [xmin,fmin]=Risenbriock_Method(x0)

epsilon=1e-5;
x_k=x0;
k=0;
n=length(x0);
D=eye(n);
Lambda=zeros(n,1);

while 1
    % orthogonal search
    z_j=x_k;
    for j=1:n
        d_j=D(:,j);    
        lambda_j=fminbnd(@(lambda) theta(lambda,z_j,d_j),-10,10);
        Lambda(j)=lambda_j;
        z_j=z_j+lambda_j*d_j;
    end
    x_kplus1=z_j;
    
    % stop criteria
    if (norm(x_kplus1-x_k)<epsilon) && (objective_fun(x_kplus1)-objective_fun(x_k)<epsilon)
        xmin=x_kplus1;
        fmin=objective_fun(xmin);
        k
        return;
    end
    
    % Gram-Schmidt procedure
    D=Gram_Schmidt_Procedure(D,Lambda);
    
    % iteration
    x_k=x_kplus1;
    k=k+1;
end

施密特正交化的过程：

function D=Gram_Schmidt_Procedure(D,lambda)

n=length(lambda);
A=zeros(n);
B=zeros(n);
sum=zeros(n,1);

for j=1:n
    if abs(lambda(j))<=0.0001
        A(:,j)=D(:,j);
    else
        for i=j:n
            A(:,j)=A(:,j)+lambda(i)*D(:,i);
        end
    end
end
for j=1:n
    if j==1
        B(:,j)=A(:,j);
        D(:,j)=B(:,j)/norm(B(:,j));
    else
        for i=1:j-1
            sum=sum+(A(:,j)'*D(:,i))*D(:,i);
        end
        B(:,j)=A(:,j)-sum;
        D(:,j)=B(:,j)/norm(B(:,j));
    end
end        

2.单纯形法

单纯形法是指n维空间具有n+1格顶点的凸多面体，以单纯性为基本单位，通过反射、扩展、压缩等方法求出一个更好的点以取代原单纯形中的最高点，构成新的单纯形，进入下一轮迭代。

单纯形法没有很好的理论性质，但他在实践中是一种很可靠的方法。

课程中代码仅仅针对二维的函数，但是实践情况肯定不止二维，局限性较大。

这篇博客中的代码均来自西南科技大学理学院最优控制与数据智能团队龙强老师的课程，仅作个人学习使用，具体链接：GitHub - QiangLong2017/Optimization-Theory-and-Algorithm: 用于存放《最优化理论与算法》代码与课件