最优化学习笔记4（外点罚函数法，内点罚函数法）

考虑问题：

 1.外点罚函数法

基本思想：

将约束优化问题转化成无约束优化问题。由目标函数和约束函数组成辅助函数，使其既能满足约束又能使目标函数值下降。罚函数的基本任务是对满足约束的点不作惩罚，对不满足约束的迭代点进行惩罚。外点罚函数法可以从不满足约束的初始点出发，迭代点对约束的违背程度越大，罚函数的惩罚就越大。

原理：

 代码：

%-------------------------------------
% Exterior penality function method
%-------------------------------------
function [xstar,ystar] = exteriorPenalty(funObj,funCon,x0)

sigma = 1;
c = 2;
epsilon = 0.01;
x = x0;

while 1
    % Constrate the penality term as a function
    penTerm = penalityTerm(funCon,sigma);
    
    % Constrate the exterior penality function
    penFun = penalityFunction(funObj,penTerm);
    
    % Solve auxiliary problem
    x = fminsearch(penFun,x);
    
    if penTerm(x) < epsilon
        % x is a K-T point
        xstar = x;
        ystar = funObj(x);
        fprintf('sigma = %f',sigma)
        return
    else
        % Increase penality factor
        sigma = c*sigma;
    end
end

%-------------------------------------
% Constrate the penality term as a function
%-------------------------------------
function penTerm = penalityTerm(funCon,sigma)
y = @(x) funCon(x);
penTerm = @(x) sigma*(sum(max(0,-y(x)).^2));

%-------------------------------------
% Constrate the exterior penality function
%-------------------------------------
function penFun = penalityFunction(funObj,penTerm)
penFun = @(x) funObj(x)+penTerm(x);

 目标函数：

function [y,g] = objFun(x)
y = (x(1)-1)^2+x(2)^2;
g = [2*(x(1)-1);2*x(2)];

 约束函数：

function y = conFun(x)
y = x(2)-1;

主函数：

x0 = [0;0];
funObj = @(x) objFun(x);
funCon = @(x) conFun(x);
[xstar,ystar] = exteriorPenalty(funObj,funCon,x0)

算法流程：

2.内点罚函数法

 基本思想：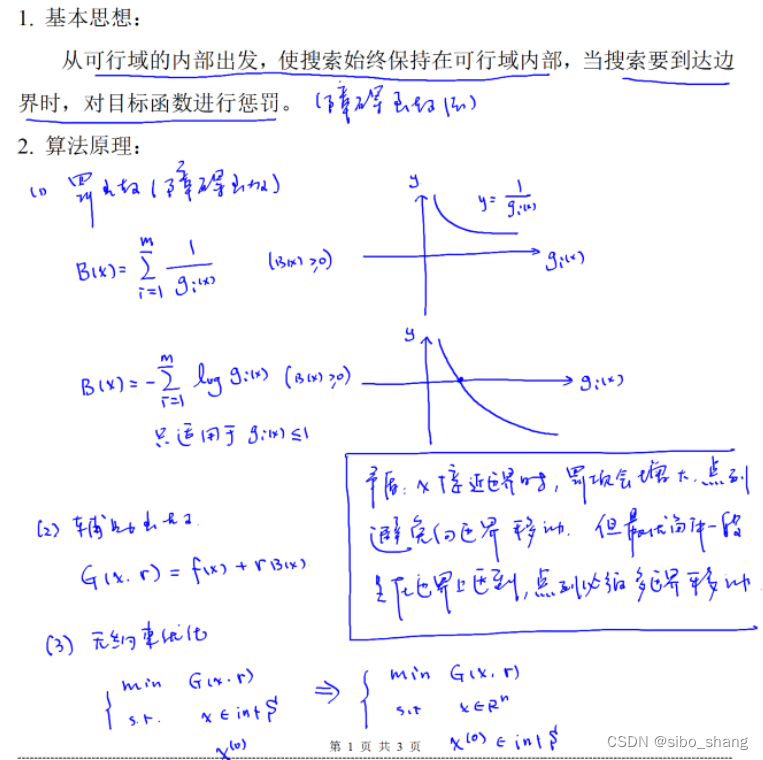

算法流程：

 

代码 

外点罚函数函数：

%-------------------------------------
% Barrier function method
%-------------------------------------
function [xstar,ystar] = barrierFunctionMethod(funObj,funCon,lb,ub)

r = 5;
beta = 0.5;
epsilon = 0.01;

% Initial feasible point
x = iniFeaPoi(funCon,lb,ub);

while 1
    % Constrate the barrier term
    barTerm = barrierTerm(funCon,r);
    
    % Constrate the barrier function
    barFun = barrierFunction(funObj,barTerm);
    
    % Solve auxiliary problem
    x = fminsearch(barFun,x);
    con = funCon(x);
    fprintf('r = %f，barTerm = %f, y = %f\n',r,barTerm(x),con(1))
    
    if barTerm(x) < epsilon
        % x is a solution
        xstar = x;
        ystar = funObj(x);
        fprintf('r = %f，barTerm = %f%',r,barTerm(x))
        return
    else
        % Decrease barrier factor
        r = beta*r;
    end
end

%-------------------------------------
% Initial feasible point
%-------------------------------------
function x = iniFeaPoi(funCon,lb,ub)
while 1
    x = lb+rand*(ub-lb);
    if all(funCon(x) >= 0)
        break
    end
end

%-------------------------------------
% Constrate the barrier term
%-------------------------------------
function barTerm = barrierTerm(funCon,r)
y = @(x) funCon(x)+0.01;
barTerm = @(x) r*(sum(1./y(x)));
% barTerm = @(x) -r*(sum(log(y(x))));

%-------------------------------------
% Constrate the exterior penality function
%-------------------------------------
function barFun = barrierFunction(funObj,barTerm)
barFun = @(x) funObj(x)+barTerm(x);

 约束条件：

function y = conFun(x)
y = [x(1)-1;x(2)];

目标函数：

function [y,g] = objFun(x)
y = (1/12)*(x(1)+1)^3+x(2);
g = [(1/4)*(x(1)+1)^2;1];

主函数：

funObj = @(x) objFun(x);
funCon = @(x) conFun(x);
lb = [-10;-10];
ub = [10;10];
[xstar,ystar] = barrierFunctionMethod(funObj,funCon,lb,ub)

总结：

 外点法和内点法均采用序列无约束极小化技巧，方法简单，使用方便，并能够用来求解导数不存在的问题，因此这种算法对实际工作者确有吸引力，而且已经得到较广泛的应用。但是，上述的罚函数法存在固有的缺点，随着罚因子趋向于极限，罚函数的Hesse矩阵的条件数无限增大，因而越来越变得病态，给无约束极小化带来很大困难。

这篇博客中的内容和代码均来自西南科技大学理学院最优控制与数据智能团队龙强老师的课程，仅作个人学习使用，具体链接：GitHub - QiangLong2017/Optimization-Theory-and-Algorithm: 用于存放《最优化理论与算法》代码与课件