本文是对Yann Lecun大神的经典论文“Gradient-Based Learning Applied to Document Recognition”的阅读笔记之一,主要介绍LeNet的结构以及参数个数的计算,上一篇博客介绍的CNN设计原理。作者才疏学浅,还望指教。
LeNet-5
引用自原论文“Gradient-Based Learning Applied to Document Recognition”
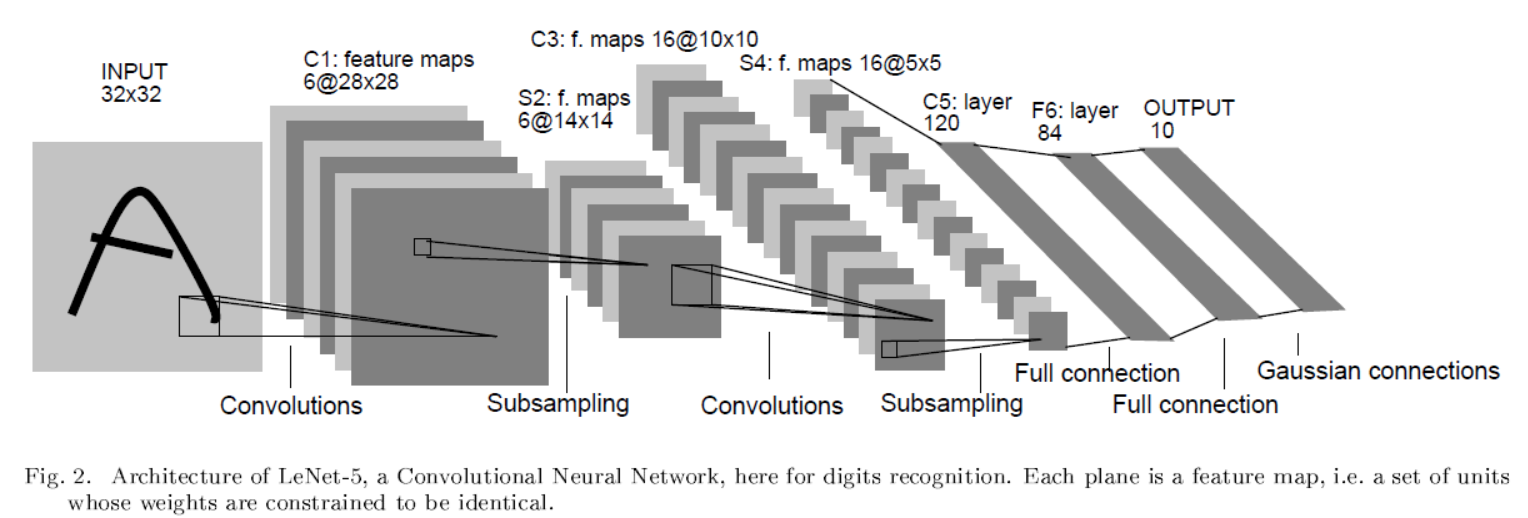
上图即为LeNet-5的结构,整体上是CNN–>max_pooling–>CNN–>max_pooling–>CNN–>fully_connect。最后一层图中表示为高斯链接层,我理解为是对OUTPUT的另一种表述(常见的表述为one of N)。
1. 数据输入
输入是32x32pixel的图像,其中而数据库中是20x20的信息在28x28pixel的中心。拓展图像是为了高层特征可以位于高层感受野中心。例如图中A的上方的拐点,如果没有拓展图像输入,则其对应在S2中的位置很有可能位于feature map的最上方,无法处于任何感受野的中心。
输入中白值为-0.1,黑值为1.175,是为了整体上均值为0,方差为1,从而加速收敛。
2. 隐藏层
- C1的CNN卷积层,kernel size=5x5,步长为1,无填充,生成6个feature map。
1.1. 因为无填充,所以生成feature map的长宽都减去(5(kernel size)-1=4),所以为(32-4)x(32-4)=28x28。
1.2. 参数个数为(5x5+1)x6=156(其中5x5对应kernel size,+1为bias,6为feature map 数目)。
1.3. 连接数为156x28x28=122304(156为参数个数,其中feature map上每个像素点对应156个链接)。 - S1为降采样层,kernel size=2x2,步长为2,无填充。
2.1. 新生成的feature map为28/2x28/2=14x14pixels。
2.2. 参数个数为 6x(1+1)=12。(因为LeNet-5采用的sigmoid(a*average(x)+b)作为池化函数)
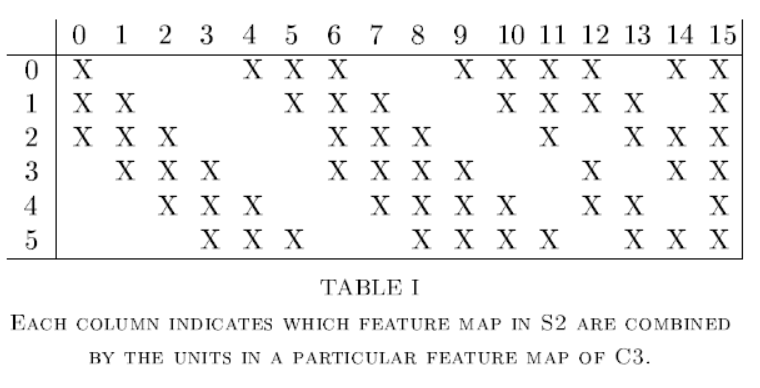
2.3. 链接个数为6x14x14x(2x2+1)=5880。六个feature map,总共6x14x14个feature,每个feature由4个C2特征+1个bias。 - C2为CNN卷积层,kernel size=5x5,步长为1,无填充,生成16个feature map。C2的feature map不是由全部的S1 feature map生成,对应关系如下图:
“引用自原论文“Gradient-Based Learning Applied to Document Recognition””
3.1. 不全部连接的原因有两个:a. 控制参数个数 b. 打破对称性,期望学得互补的特征。
3.2. 新生成的feature map的size为14-(5-1)=10.
3.3. 参数个数为(5x5x3+1)x6+(5x5x4+1)x9+(5x5x6+1)=1516个。括号内部为kernel_size x kernel_size x feature_map_num + bias_num,表示从feature_map_size卷积得到的feature map所需要的参数个数;括号外为相应得到feature map的数目。
3.4. 链接个数为1516x10x10=151600个。其中1516为参数个数,10为新生成的feature map的size。 - S2为降采样层,kernel size=2x2,步长为2,无填充。
4.1. 新生成feature map的size为10/2=5
4.2. 参数个数为16x2=32。
4.3. 链接个数为5x5x16x(2x2+1)=2000。(5为新生成feature map的size,16为feature map的数目,2为kernel size,1为bias。 - C5为卷积层,kernel size=5x5,步长为1,无填充,全连接生成120个feature map。
5.1. 新生成feature map的size为5-(5-1)=1。
5.2. 参数个数为120x(5x5x16+1)=48120。
5.3. 链接个数等于参数个数,因为新生成feature map的size为1。 - F6全连接层,输入120个,输出84个
6.1. 输出节点数目由OUTPUT表述有关,详见输出表述。
6.2. 链接个数=参数个数=(120+1)x84,其中+1为bias。
6.3. 全连接层的激活函数为Atanh(Sx),其中A和S为超参数。
3. 输出表述
输出表述是将给定的label转换为一个向量,作为神经网络的真值。传统常见的方法为1 of N,这里不在赘述。
文章中是把图片对应的字符在7x12的bitmap上画出,白值为-1,黑值为1,其中84个像素平铺之后的向量对应为相应字符的表述,作为真值与F6连接。这样做的优点有:
1. 对于识别全打印的ASCII字符有用(单独数字无用)
2. 外表相近的字符如”i”和”1”等在这种表述中也相近,这样在神经网络之后加入个依靠语义更正的系统,可以提高准确率。
3. 1 of N的表述在N大于几十的时候就会表现不好。
4. 这样的表示可以用于拒绝非字符,而不是所有的都识别为字符。
设置“白值为-1,黑值为1”的原因是为了把函数限定在sigmoid函数斜率较大的区域,否则收敛较慢,而且会ill-conditioning。这个1的选择是由A得出,使得sigmoid的二次导最大(作者的猜测,还没有看论文验证))






















 1035
1035

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








