线性回归可以说是机器学习算法中最基础的一种了,而且我想大部分人在没有听说过机器学习的时候就已经学过或者用过这样的一种方法了。
简单的来说,线性回归就是利用一系列特征的一个线性组合来进行预测,只有一个特征的时候,通常称为一元线性回归,多个特征则称为多元线性回归,通常表示如下。
不过通常我们对线性回归都有一个直观的误解,因为它的形式是线性的,所以总感觉它拟合的是一条直线(平面,超平面……),这样的话对一些不是线性关系数据的拟合表现会很差。但其实这里的x1x2并不只能是自变量本身,他们代表的是特征,其取值是我们可以构造的任意特征,就拿x1x2两个自变量来说,我们可以构造(x1,x2,x1x2,x1**2,x2**2)这5个特征来对数据进行拟合,这样即使有高次属性也能通过线性回归进行较好的拟合。所以,它之所以叫线性回归是因为它是对特征的线性组合而不是对自变量的简单线性组合。
理解了线性回归的概念之后,我们就要讨论如何来求这个参数theta了,我们如何制定一个标准来表征这组参数对数据拟合的好坏程度呢?最直接的想法就是用预测值减去实际值的平方和来表示拟合的好坏,这个值越小拟合程度越高。
当然了,不可否认,这种直观的认识确实是正确的……那总要有个科学的解释吧!Ok,一步步来,我们从最大似然的角度来证明,首先对于每个样本的误差都是独立同分布的,所以最后的整体误差肯定服从一个均值为0,方差sigma**2的高斯分布。
所以啊,我们的直觉是和科学一致的,有时候真是不信自己不行。
好的,有了这样一个损失函数之后,我们的目标就是最小化这个损失函数。比较明显的是,这个损失函数是关于theta的一个凸函数,它的极值点就是我们要求的最小值,这里其实为梯度下降法埋下了一个伏笔,我们后面再说,先跟着求极值的思路来,那么就是求导找驻点。
好了,到这里我们已经求出了最佳参数theta,(x.Tx)是半正定的,大部分时候可逆,当然不排除的有的时候这个(x.Tx)不可逆,所以有的时候需要加个正则项保证正定可逆,同时也能防止过拟合,这个一会儿再说。
那么先前也说到了,求这个损失函数还有一种方法,就是所谓的梯度下降。首先为什么叫梯度下降呢?因为梯度是函数变化最快的方向,所以沿着梯度走一定能最快的进入到驻点。而线性回归的损失函数是个关于theta的凸函数,所以它的住店一定就是它的全局最小值。
根据 上面的公式,迭代计算,theta收敛后就是我们要求的最佳参数。像上图这样每次求梯度都用到所有样本的方法我们称之为批量梯度下降(Batch gradient decent),对于线性回归,这样做是一定能够收敛的,但有时候我们要做在线处理,还有样本量非常巨大的时候,BGD就不太适用了,我们其实也可以拿一个样本就下降一次,这样虽然不能保证整体损失函数每次都下降,但是计算量小了很多而且适合做在线处理,这种方法我们称之为随机梯度下降(Stochastic gradient decent)两种方法表示如下。
接下来我们自己构造一组数据进行一次简单的线性回归。在0到10上取10个数,利用公式2*x+5构造数据,并加入一定的扰动,构造对应的y数据。然后分别利用sklearn的LinearRegression和公式计算最优参数,比较两者的异同。
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import matplotlib as mpl
np.random.seed(0)
N=10
x=np.linspace(0,10,N)
y=2*x+5+np.random.randn(N)*0.1
model=LinearRegression(fit_intercept=False)
degree=PolynomialFeatures(degree=1)
xfeature=degree.fit_transform(x.reshape(-1,1))
model.fit(xfeature,y)
print '线性回归的参数是\n',model.coef_
#直接法计算回归参数
print '直接计算最优参数\n',np.linalg.inv(xfeature.T.dot(xfeature)).dot(xfeature.T.dot(y))
x_test=np.linspace(-2,12,100)
x_test.shape=-1,1
x_testf=degree.transform(x_test)
y_predict=model.predict(x_testf)
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.plot(x_test,y_predict,'r-',label=u'预测数据')
plt.plot(x,y,'g*',label=u'原始数据')
plt.legend(loc='lower right')
plt.title(u'线性回归预测', fontsize=18)
plt.grid()
plt.show()
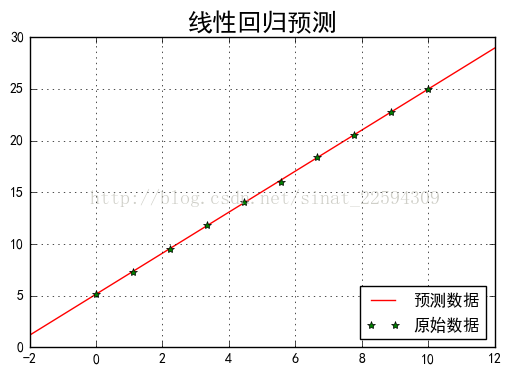
输出是
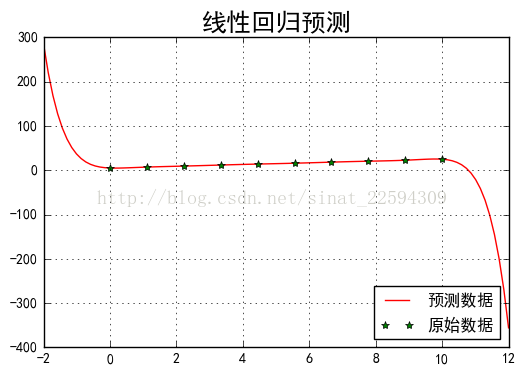
上面的例子其实我们最后拟合的直线并不过所有点,而总是有那么一点偏差,其实对于10个点而已,我肯定能找到一个9阶的多项式来过所有的点。比如我们把上面代码中的degree改成9,输出如下
所谓正则化,就是说我们在损失函数加入关于参数theta的项,防止某些不重要的参数过大影响整体模型的效果。在这里正则项有两种形式
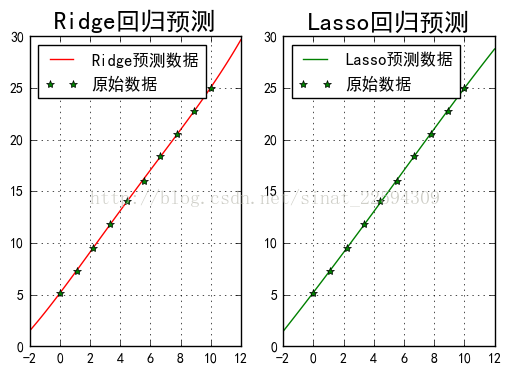
这两种正则方式都可以有效地抑制高阶量对模型的影响,防止模型过于复杂,影响预测的效果,接下来我们用同样的9阶回归不过加入正则项,看看最佳参数有何变化
import numpy as np
from sklearn.linear_model import RidgeCV, LassoCV
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import matplotlib as mpl
np.random.seed(0)
N=10
x=np.linspace(0,10,N)
y=2*x+5+np.random.randn(N)*0.1
model1=RidgeCV(alphas=np.logspace(-5, 0, 50), fit_intercept=False)
degree=PolynomialFeatures(degree=9)
xfeature=degree.fit_transform(x.reshape(-1,1))
model1.fit(xfeature,y)
print 'Ridge回归的参数是\n',model1.coef_
model2=LassoCV(alphas=np.logspace(-5, 0, 50), fit_intercept=False)
model2.fit(xfeature,y)
print 'Lasso回归的参数是\n',model.coef_
x_test=np.linspace(-2,12,100)
x_test.shape=-1,1
x_testf=degree.transform(x_test)
y_predict1=model1.predict(x_testf)
y_predict2=model2.predict(x_testf)
mpl.rcParams['font.sans-serif'] = [u'simHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.subplot(121)
plt.plot(x_test,y_predict1,'r-',label=u'Ridge预测数据')
plt.plot(x,y,'g*',label=u'原始数据')
plt.legend(loc='upper left')
plt.title(u'Ridge回归预测', fontsize=18)
plt.grid()
plt.subplot(122)
plt.plot(x_test,y_predict2,'g-',label=u'Lasso预测数据')
plt.plot(x,y,'g*',label=u'原始数据')
plt.legend(loc='upper left')
plt.title(u'Lasso回归预测', fontsize=18)
plt.grid()
plt.show()
好了,这大概就是线性回归部分的内容,损失函数的由来,梯度下降法,正则化处理,希望对大家有帮助,也欢迎指教。








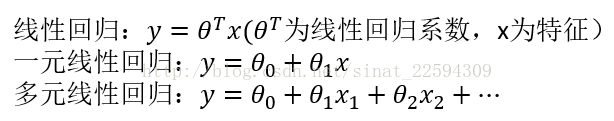
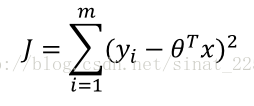
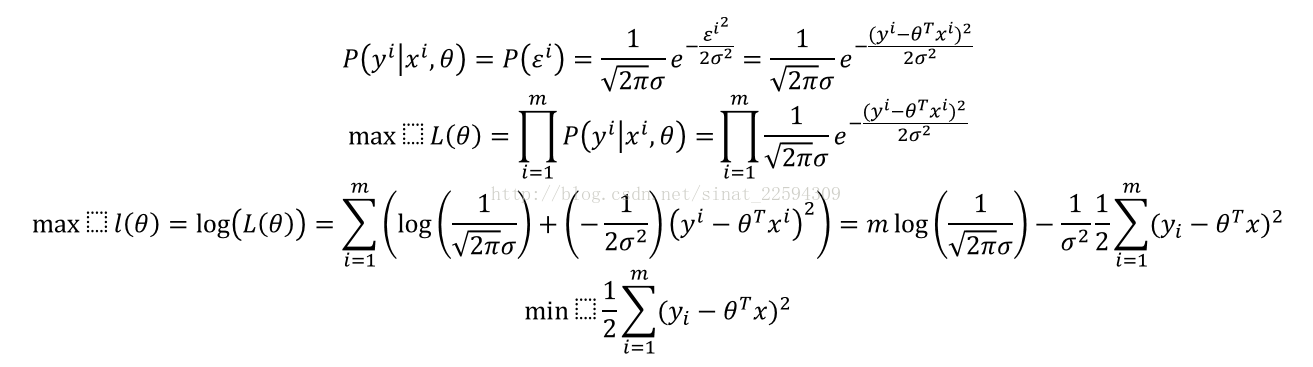
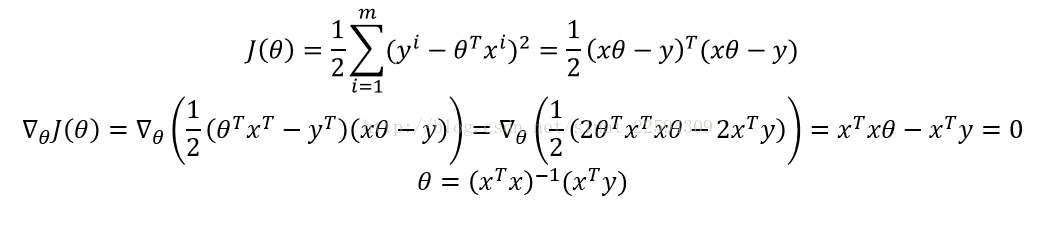
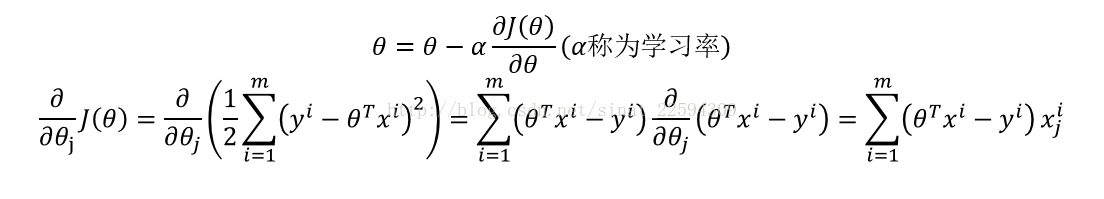
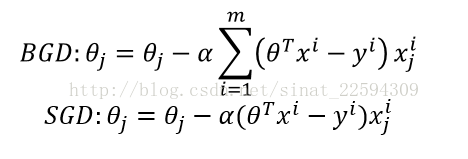
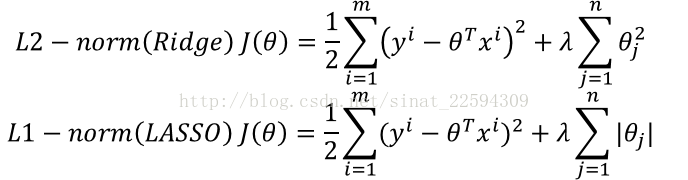














 1120
1120

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








