在上一篇博客里,我们讨论了关于Bagging的内容,其原理是从现有数据中有放回抽取若干个样本构建分类器,重复若干次建立若干个分类器进行投票,今天我们来讨论另一种算法:提升(Boost)。
简单地来说,提升就是指每一步我都产生一个弱预测模型,然后加权累加到总模型中,然后每一步弱预测模型生成的的依据都是损失函数的负梯度方向,这样若干步以后就可以达到逼近损失函数局部最小值的目标。
下面开始要不说人话了,我们来详细讨论一下Boost算法。首先Boost肯定是一个加法模型,它是由若干个基函数及其权值乘积之和的累加,即
其中b是基函数,beta是基函数的系数,这就是我们最终分类器的样子,现在的目标就是想办法使损失函数的期望取最小值,也就是
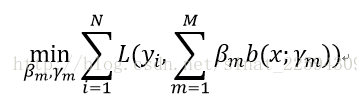
一下子对这M个分类器同时实行优化,显然不太现实,这问题也太复杂了,所以人们想了一个略微折中的办法,因为是加法模型,所以我每一步只对其中一个基函数及其系数进行求解,这样逐步逼近损失函数的最小值,也就是说
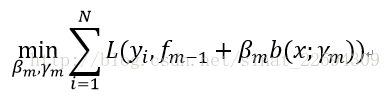
那聪明的你一定想到了,要使损失函数最小,那就得使新加的这一项刚好等于损失函数的负梯度,这样不就一步一步使得损失函数最快下降了吗?没错,就是这样,那么就有了
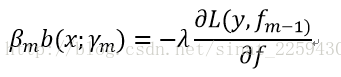
Lambda是我随便写的一个参数,可以和beta合并表示步长,那么对于这个基函数而言,其实它就是关于x和这个函数梯度的一个拟合,然后步长的选择可以根据线性搜索法,即寻找在这个梯度上下降到最小值的那个步长,这样可以尽快逼近损失函数的最小值。
到这里,梯度提升的原理其实就讲完了,接下来我们就讲几个实际情况中的特例,包括梯度下降提升树(GDBT),自适应提升(AdaBoost),以及Kaggle竞赛的王者极限提升?翻译不知道对不对,就是(XGBoost)。
第一个,GDBT。
对于这个,一旦对上面梯度提升的想法理解了那就很容易解释了。首先既然是树,那么它的基函数肯定就是决策树啦,而损失函数则是根据我们具体的问题去分析,但方法都一样,最终都走上了梯度下降的老路,比如说进行到第m步的时候,首先计算残差








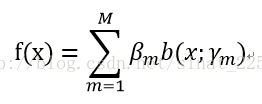
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








