关于地球上两点距离公式讨论

Flat Earth距离 （近似为平面）

• 带修正的计算方法

$$d_f=R\sqrt{({\theta }_A-{\theta }_B{)}^2+\cos \left[\frac{{\theta }_A+{\theta }_B}{2}\right]\Delta {\lambda }^2}$$
其中 R 是地球平均半径（由参数 PROJ_MEAN_RADIUS 控制）， θ 是纬度， Δλ=λA−λB
是经度差。式中地理坐标的单位均是弧度，且需要考虑到跨越经度的周期性问题。

这个公式是用来计算平面地球模型下两个地点之间的距离的近似公式，其中：

• d_f：表示两个地点之间的平面距离 (flat distance)
• R：表示地球的半径
• θ_A、θ_B：表示两个地点的纬度 (latitude)，以弧度为单位
• Δλ：表示两个地点的经度差 (longitude difference)，以弧度为单位

公式中的第一项$$({\theta }_A-{\theta }_B{)}^2$$是计算纬度差的平方，代表纬度方向上的距离。

公式中的第二项$$\cos \left[\frac{{\theta }_A+{\theta }_B}{2}\right]\Delta {\lambda }^2$$是计算经度差的平方的修正项。其中，$$\Delta {\lambda }^2$$ 是经度差的平方，代表经度方向上的距离差。而$$\cos \left[\frac{{\theta }_A+{\theta }_B}{2}\right]$$是一个修正系数，用来考虑纬度对经度距离的影响。由于地球的经线在赤道处距离比较远，而在极地附近距离较近，因此需要对经度差进行修正。

在这个公式下，假设地球是一个平面，而不考虑其真实的球形曲度。这种计算方法仅适用于近距离的近似计算，并不能准确地表示地球表面两点之间的实际距离。对于较大距离或需要高精度的距离计算，应使用更精确的距离计算方法，比如球面三角计算公式（例如Vincenty公式）。

需要注意的是，公式中的角度单位为弧度，而不是度数。所以在计算之前需要将纬度和经度的度数转换为弧度。

该方法的特点是计算速度快但精度不高，适用于纬度相差不大且对计算效率要求比较高的情况。

• 勾股定理

Flat Earth距离的计算原理非常简单，即通过计算两个地点之间的直线距离来近似表示它们之间的距离。这可以通过使用两点之间的直角三角形的勾股定理来实现。

以下是一个使用C语言实现的计算两个地理坐标点之间Flat Earth距离的代码示例：

#include <stdio.h>
#include <math.h>

// 定义经纬度结构体
struct Coordinate {
    double lat;  // 纬度
    double lon;  // 经度
};

// 函数：计算两个坐标点之间的Flat Earth距离
double calculate_distance(struct Coordinate point1, struct Coordinate point2) {
    double lat_diff = fabs(point1.lat - point2.lat);
    double lon_diff = fabs(point1.lon - point2.lon);

    // 距离的计算使用勾股定理
    double distance = sqrt(pow(lat_diff, 2) + pow(lon_diff, 2));

    return distance;
}

int main() {
    // 定义两个地理坐标点
    struct Coordinate point1 = {50.0, 10.0};  // 第一个点的纬度和经度
    struct Coordinate point2 = {52.0, 14.0};  // 第二个点的纬度和经度

    // 计算两个坐标点之间的距离
    double distance = calculate_distance(point1, point2);

    // 打印距离结果
    printf("Flat Earth距离: %lf\n", distance);

    return 0;
}

• 应用范围讨论

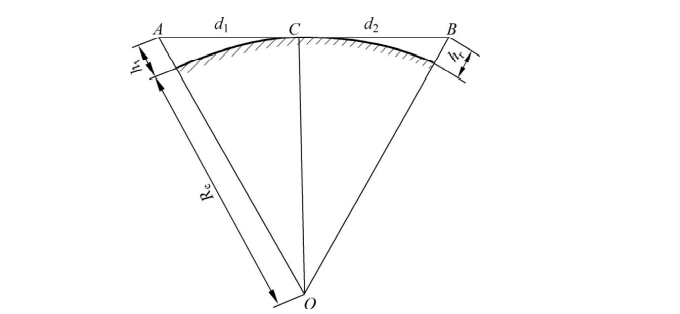
他山之石，可以攻玉石。
由于知晓一点无线电传输原理，在U段的无线电就是视距传输。
所以搞来关于Loro的计算成果无线电地面通信的极限距离问题

$$d_f=4.12\sqrt{h}$$
其中
h:人身高（m）
$d_f$:视距（km）
最终：1.5m的人4-5km的视距。

范围参考：结论：目视极限距离是 4515 米

大圆路径距离-Haversine 公式 （近似为球）

• Haversine公式

$$d=2R\cdot {\sin }^{-1}\left(\sqrt{{\sin }^2\left(\frac{\Delta \theta }{2}\right)+\cos ({\theta }_1)\cdot \cos ({\theta }_2)\cdot {\sin }^2\left(\frac{\Delta \lambda }{2}\right)}\right)$$
其中：
$d$ 表示两个地点之间的大圆路径距离（Haversine distance），
$\mathbb{R}$ 表示地球的半径，
${\theta }_1$和 ${\theta }_2$ 分别表示两个地点的纬度，
$\Delta \theta$表示纬度差，以弧度为单位。
$\Delta \lambda$ 表示经度差,以弧度为单位。
该方法将地球近似为一个半径为R的球，地球上任意两点 A 和 B 的大圆路径距离可以用 Haversine 公式 计算

• 代码

下面是使用C语言实现Haversine公式的示例代码：

#include <stdio.h>
#include <math.h>

#define R 6371 // 地球半径（单位：千米）

double toRadians(double degree) {
    return degree * M_PI / 180.0;
}

double haversine(double lat1, double lon1, double lat2, double lon2) {
    double dLat = toRadians(lat2 - lat1);
    double dLon = toRadians(lon2 - lon1);

    double a = sin(dLat/2) * sin(dLat/2) +
               cos(toRadians(lat1)) * cos(toRadians(lat2)) *
               sin(dLon/2) * sin(dLon/2);
    double c = 2 * atan2(sqrt(a), sqrt(1-a));
  
    double distance = R * c;
    return distance;
}

int main() {
    double lat1, lon1, lat2, lon2;

    printf("请输入第一个地点的纬度和经度（空格分隔）：");
    scanf("%lf %lf", &lat1, &lon1);
    printf("请输入第二个地点的纬度和经度（空格分隔）：");
    scanf("%lf %lf", &lat2, &lon2);

    double distance = haversine(lat1, lon1, lat2, lon2);
    printf("两个地点之间的距离为：%.2lf千米\n", distance);

    return 0;
}

这个示例程序首先定义了一个常量 R 表示地球的半径（单位：千米），然后实现了一个辅助函数 toRadians，用于将角度转换为弧度。接下来，haversine 函数接收两个地点的纬度和经度，并根据Haversine公式计算两者之间的距离。最后，在 main 函数中，用户输入两个地点的经纬度，然后调用 haversine 函数计算距离，并将结果输出到屏幕上。

测地距离-Vincenty 公式 （完全椭球公式）

参考

16.6 三种距离计算方式 — GMT中文手册
Vincenty solutions算法