Benders decompositon学习笔记记录

Benders分解作为3大分解算法之一，听过很久了。好像目前最新的是Benders逻辑分解，比着Benders分解又升级进步了。UTD24中有一些相关的文章，我也在慢慢拜读中。

1.常见的分解算法

经典的3大分解算法分别是：

（1）Benders decomposition (主要思想是行生成+割平面方法)；
（2）Dantzig-Wolfe decomposition (主要思想其实就是列生成)；
（3）Lagrangian decomposition (主要思想是 Lagrangian relaxation)。

分解算法指的是，把原来的问题拆分成若干小问题，拆分的原因是因为小问题求解起来比直接求解原来的大规模问题难度要低。求解问题往往规模一大，就很难进行求解了。拆分的学术用语是：分解。

但是，分解后的小问题和原来问题一致吗？如何保证是一致的，我们的目的是求解原来的问题，所以一定要保证分解后的模型和原来模型一致，从而保证全局最优。再者，分解后的若干问题彼此之间是否有交互？怎么建立交互关系？这些都是我们需要考虑的问题，也是分解算法的重心。其实，前面说的是分解拆解或者叫解耦，后面说的是耦合。也就是说，解耦+耦合是分解算法的核心。

其实，不同算法的区别就在于解耦+耦合的不同。如Dantzig-Wolfe decomposition和Benders decomposition是根据模型的特殊结构，将模型分解为更容易求解的小问题，通过小问题之间的迭代求解和交互，最终达到精确求解模型的目的的精确算法。但是二者的分解思路并不相同。Dantzig-Wolfe decomposition是基于一个表示定理得来的分解方法，该方法需要MIP的约束矩阵符合块角状的特征，通用性有限，使用之前需要考察模型是否符合该结构。而Benders decomposition实际上是较为通用的分解框架，CPLEX中也包含了Benders decomposition的算法组件，用户可以自己定制分解策略。Benders decomposition的主要思想是，将较复杂的模型分解成为两部分，分别求解两部分都较为容易，通过两部分之间的交互迭代，最终算法得到收敛，得到最优解。

2.Benders分解算法的思路

上面提到Benders分解算法的主要思想是行生成+割平面。简单问题每次返回或者说生成割平面，然后把这个割平面添加为复杂问题的约束中，也就是变为新的一行。因为模型中通常约束为行，解为列。同时，割平面根据简单问题（对偶问题）的求解结果不同，可以分为最优割和可行割，分别添加到复杂问题中。简单问题可以直接求出最优解的，对应为最优割；无界或者不可行的，对应为可行割。

也就是说，简单问题会生成割平面；然后割平面添加到复杂问题中；复杂问题求解得到的结果再传给简单问题；简单问题继续生成割平面......如此不断循环。同时，在循环的过程中，会不断更新原来问题的上下界，当上下界的Gap处于可以接受的误差范围时，求解终止，吐出最后的方案。

3.Benders算法的数学推导

因为自己也在学习过程中，所以写的可能偏简单。

考虑以下模型，其中x是连续变量，y是整数变量。那么我们可以把x看做是简单变量，y是复杂的变量。因为只单纯看x，模型是LP，可以在多项式时间求解，如单纯形法；而y是整数变量，当问题规模变大时，往往很难进行求解，因为大多数IP都是NP难的。也就是说，y这个复杂变量让问题变得不好求解了。

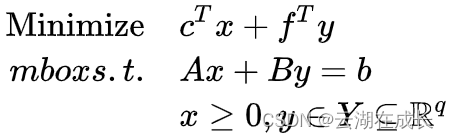
那么我们能不能先搞定复杂变量，那么只剩余简单变量的问题就好求解了。这就是Benders分解的思路来源。先搞定复杂变量，再求解简单变量的问题，再通过秋后算账的方式（割平面）把没考虑的因素再考虑进来，如此进行求解。

假如给定一个y为，那么上述问题可以表示为如下模型。很明显可以看出该LP问题很容易求解，比着原来问题求解难度降低了很多。其实这个模型又被称为子问题SP：subproblem。

那么，原来的模型可以写做如下模型。这个模型其实是主问题MP：master problem。

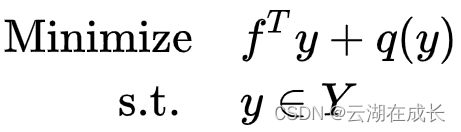
那么求解思路来了，就是不断在主问题和子问题中进行交互。如此来求解原问题。

同时，我们可以看到，因为每次MP都会生成新的y，那么SP的存在y的约束就在变化，对应着子问题的可行域也在不断变化。因此我们考虑SP的对偶问题Dual SP。如此以来，y会出现在目标函数上，那么求解上又变简单了。

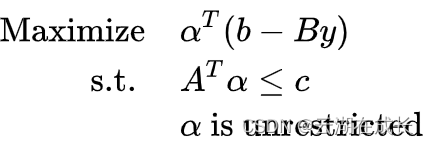
 注意到上述Dual SP的可行域是不变的（因为约束不变），每次传送不同的y只影响到目标函数值。根据LP理论，该问题对应的可行域是个多面体，有：

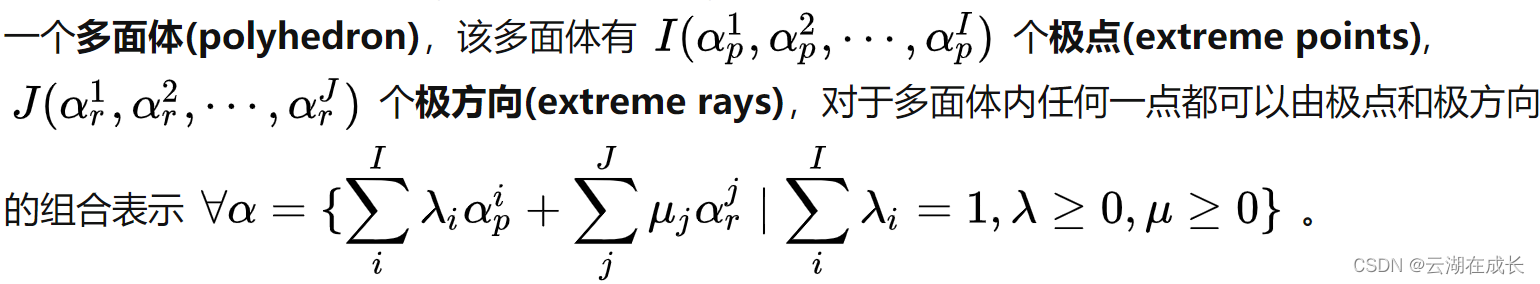
• 若可行域非空且无界，最优解一定可以由可行域的某个极方向表示。
• 若可行域非空且有界，最优解一定在可行域的某个极点上。
• 若可行域为空集，其对偶问题无界，则原问题也无界，模型目标值可以取到无穷小，失去求解意义。

 那么原问题可以转化为：

根据以上理论，那么可以列出以下求解过程：

（1）按照变量难易，拆分为一个主问题MP，和一个子问题SP。

（2）求解MP，得到对应的y*和z*，将y*传入到SP中。若SP得到无界解，说明对于该无界解对应的可行解是一个极方向，所有的极射线可以得到可行割，可以通过gurobi调用对应的命令直接获取。若SP得到有界可行解，则得到最优割。

因为Dual SP的解分为三种情形：无解、有可行解但无界（无界解）、有可行解且有界（有界解）。

第一种，当Dual SP存在无界解时，由弱对偶定理可得SP无解，说明给定的不合理，需要添加cut割掉  ，最简单的方法就是找到所违反的约束，加入master problem。而min问题存在无界解，那么添加极射线集合。

第二种，当Dual SP存在有界解时，SP也为有界解。即，来继续优化MP，让MP往更小的方向前进。

（3）将可行割/最优割添加到MP中进行求解，并更新模型上下界，若上下界误差在可接受的范围内，则获得最优解。

这里需要关注的是：上下界的更新方式。每次给定y*，求解SP得到的x，即（x,y），也就是说fy+q(y)得到的是原问题的一个可行解，也就是上界；同时因为每次只是添加一部分割平面，可以提供一个下界。换句话说，UB=min{UB，fy+q(y)}；而LB是通过cut进行更新的。

• 若添加 feasibility cut，求解 relaxed master problem最优目标函数值为MIP下界
• 若添加 optimality cut，求解 relaxed master problem最优目标函数值为MIP上界

后续再补充。

参考文章：

taskin_benders.pdf (boun.edu.tr)（最好看看这个）

优化 | Benders Decomposition - 知乎 (zhihu.com)

Benders Decomposition学习笔记 - 知乎 (zhihu.com)

【整数规划算法】Benders 分解（理论分析+Python代码实现）_王源WANGYuan的博客-CSDN博客 Benders分解(Benders Decomposition)算法：算法原理+具体算例_出淤泥的博客-CSDN博客_benders分解算法 优化算法 | Benders Decomposition: 一份让你满意的【入门-编程实战-深入理解】的学习笔记 (qq.com)