逻辑benders分解

目录

1.可行割

（1）组合benders割（本质是cover cut 覆盖割）

（2）最小可行割（minimal infeasible set，MIS） 

2.最优割

（1）常规最优割

（2）analytical benders cut——需要严格的数学证明

注：

LBBD的两种实现方式：

branch and check步骤：

---

前文综述：

benders分解算法 逻辑思路整理（加星）-CSDN博客

以下默认为min问题。

——本文主体内容和图片来自李延通老师的ppt。

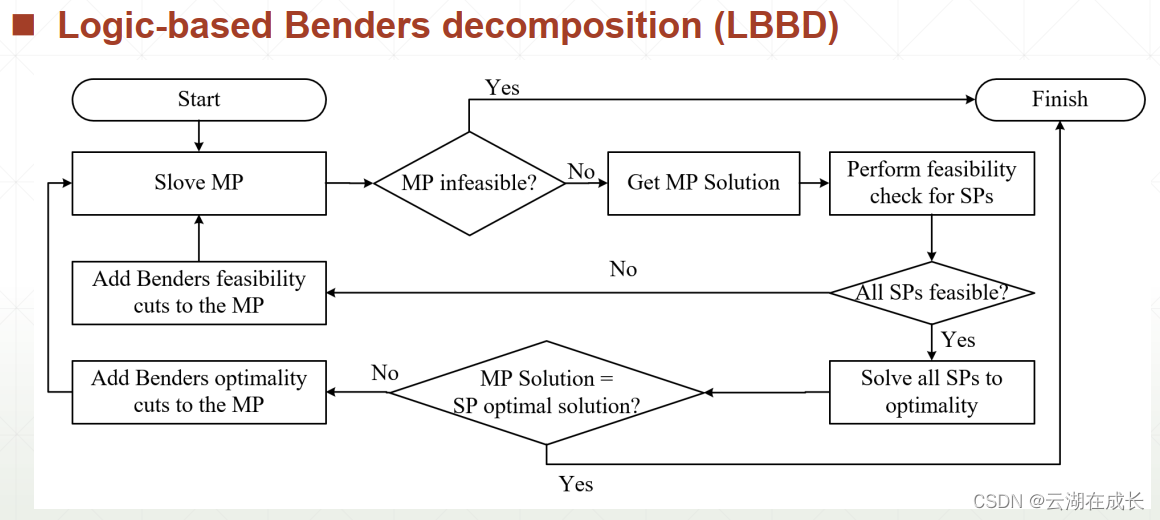
benders分解是指把问题分解为主问题和子问题。主问题松弛后得到的信息输入到子问题中，求解子问题后生成一些割加入到主问题中去。加入的割可以提升主问题的下界（主问题提供的解），继续反馈给子问题后，降低了上界（子问题提供的解），直到上下界相等，求解完成。

经典的benders分解，指的是子问题是线性规划问题；

基于整数的benders分解，指的是子问题是整数规划；

而基于逻辑的benders分解，指的是子问题返给主问题的割是根据逻辑得到的割。

对于调度问题，通常有以下几种。

1.可行割

类似背包约束。假设问题的上界是13。子问题得到的解为15，此时返回可行割。

（1）组合benders割（本质是cover cut 覆盖割）

即当前的解不合理，需要从当前被分配的工件集中去除至少1个工件。下图中M2机器至少得去除一个工件，。

将该cut加入到主问题中，告诉主问题下次必须得从中去除至少1个工件，使得新工件集合数量最多为3个。即下次主问题中必须有一个取值会有变化，从1变为0，即从原本的分配中被移除。

但是该cut效果有限，原因是，只能保证删除1个。删除1个后就失效了。需要我们继续添加割，此时迭代步骤会变多。

因此我们想要得到更好的可行割，更强的割，希望割去更多的工件，减少了迭代反复的次数，加速算法的收敛，求解效率会提高。

（2）最小可行割（minimal infeasible set，MIS） 

最小可行割就是为了解决上述问题而产生的。它计算了每个批次最多保存的工件的个数。

首先介绍最小子集：

即当前的≥上界，但再继续删除就＜上界了，寻找这样的一个边界集合。

需要从中依次移除工件，只要解≥上界，就依次移除，即变为。继续移除，直到移除后子问题的解（上界）＜上界了，就得到最终的最小可行割，如V2所示。

2.最优割

主问题因为松弛掉部分约束，得到的是下界，是基于部分信息得到的决策。我们希望子问题得到一些割进而能提升主问题的下界。

（1）常规最优割

普适性比较强：

若下一次主问题求解时：

a）分配给机器k的工件仍为相同的一组工件，即，此时有。

告诉主问题，假如下次你仍然分配这些工件给机器k，则最大完工时间如（V5）所示。

b）分配的解有变化，假如某工件从机器k上被移除，则右边为0或负数，此时V5是无效的。

总之该式给与了一个下界。

由于上述割在被移除的时候，不等式右边直接缩减为0，因此需要考虑增强技术。常用的是分析bender割。

（2）analytical benders cut——需要严格的数学证明

以带有设置时间的UPM问题为例，通常。

分析如下：假如将工件j移除，则。则最多减少了加工时间以及可能的最大设置时间。这是最多可能减少的部分，因此为主问题提供了一个更紧的下界。

注：

LBBD的两种实现方式：

branch and check步骤：

（1）因为子问题需要多次求解，因此当主问题复杂，子问题简单时，适合用本方法。特别是branch and check法，主问题只需要求解一次。更加的适用。

（2）其它的一些加强技术包括，提升主问题的下界。因为初始主问题包含的信息很少，所以最好加入一些有效不等式，得到一些较好的下界。换句话说，有效不等式加入主问题中很有用。

（3）其它的一些加强的benders cut。