目录
运筹我们最先接触分支定界算法，也就是由Land Doig和Dakin在20实世纪60年代初提出的branch and bound算法，用在整数规划（全部决策变量是整数）中。其实用在混合整数规划（部分决策变量是整数）中也是可以的（本身混合整数规划就能够转化为整数规划）。
目前很多求解器，如cplex和gurobi就是基于分支定界算法框架设计的。
没错，分支定界只是框架。
1.基础版的分支定界算法（假设是min问题）
首先阐述下分支定界算法的思路。不像纯粹的LP问题，可行域是无限的多面体。整数规划的可行域是由一系列点组成的，直观的思路是一个个列举点，但这显然不现实。于是我们的思路是，首先找到凸包，即围绕这一系列点的最小的多面体。松弛该问题求解，假如是整数解，也就是说整数规划等同于线性规划（具有整数最优性，即系数矩阵是全幺模矩阵）。假如不是整数解，那么我们把该凸包划分为一系列的小多面体进行求解。
也就是说核心的思路是不断切分，把可行域分成较小子区域的方法。但是不能无限的切分探测下去，不然会求解很久。因此我们面对一些不可能产生更好的区域，直接舍弃。即进行剪支操作（prune）。
接下来介绍几个定理（以下假设为min问题，因为min问题比较常见，假如是max问题，直接取镜像即可）：
（1）若上界和下界相等，且上界是整数可行解，那么上界对应的可行解就是最优解。
备注：假如上界和下界差距为，即上界-下界
，那么称上界对应的可行解是一个
近似最优解。最优解显然是
=0的情况。
（2）若松弛的LP不可行，那么对应的IP也不可行；
若LP的最优解满足整数可行性条件，那么LP的最优解也是IP的最优解。
（3）假如松弛的LP问题产生的解的质量弱于IP问题，对于min问题，即LP的解>IP的解，那么直接舍弃。因为不可能产生更好的解了，松弛LP的子问题肯定比它更差。
2.分支定界算法的步骤及其注意事项
根据上述定理可以进行branch分支和bound定界操作。
2.1 具体的分支定界方法的步骤：
先对问题A进行松弛，也就是整数决策变量松弛为连续型变量，对线性规划问题B进行求解，得到问题的下界（线性规划问题约束更少，因此可行域更大，会取到不弱于IP的解）。IP问题的解一定不好于LP的解，一定是。
若LP问题满足整数条件，那么恭喜，在这里就找到了最优解。停止。（这条是针对初始问题而言的）。
同时人工观察一个可行解（满足整数约束）上界，或者直接定为无穷大也可以。
注解：这里是min问题，因此可以总结为：
所有IP问题的最好的解即为上界，即min{f(整数可行解)}为上界；
而所有LP问题的最好的解为下界，即min{f(LP可行解)}。
2.2 迭代过程，也就是分支定界方法的核心操作：
a) branch 分支：在B（LP问题）中找到不满足整数条件的，然后对其向下取整B1和向上取整B2，分为两支。注意，此处并不会丢失任何整数可行点。
b) bound 定界：对每个后续问题为一个分支表明求解结果，与其它问题的解比较。
松弛问题的目标函数最小者记为新的下界；
从符合整数条件的各分支中，找到最小的可行解作为新的上界，若没有整数可行解，还保持旧的上界不变。
c) cutoff 比较与剪枝——可以提升效率，不必像枚举法一样使得二叉树以2的幂级膨胀，同时不断剪枝，使得目前的搜索树增长得慢一些，3种场景可以剪支：
prune by bound，边界剪支。若最优解大于等于上界，剪掉这支。因为是最小化问题，那么新支得到的解（无论是否是整数解，假如是LP解，因为对应的IP问题的解会更大；假如是IP，因为有比它更好的解。实际编程求解的时候只用看LP即非整数解即可，因为IP解的意义其实在于确定上界，该点质量不足以改变上界，会被忽略）会大于目前的上界，这个分支都可以不考虑。这种情况基本出现在后续迭代过程中，通过不断剪枝缩减树叶规模。
prune by optimility，最优性剪支。若求解该节点得到的解为整数解，那么也可以减掉该支了，因为该支已经求解完毕。
prune by infeasiblity，不可行剪支。若LP问题无解，那么可行域更小的IP更无解了，剪去此支。
以上三条为剪支的三种情形。
也就是说分支定界的精髓在于分支和定界过程，使得算法的求解效率高于枚举法，同时求解结果和枚举法一样。
这种方法十分好用，因此目前大规模问题中，使用的框架都是分支定界（这里的分支指的是一组变量，并不是前述中的单变量分支了）算法。每步只求解一个子问题，然后比较再放入到主问题中去，最后找到比较好的解。这部分留到第三部分讲。
2.3 分支策略：
分支定界法的影响点主要是选择哪一个子问题进行分支？也就是说从搜索树中剩下的节点（子问题）中选择的节点会影响整个分支定界的收敛速度。比如同时碰到x1=1.55；x2=2.55，选择哪条支进行分支呢？
常用的策略是近0.5规则，也就是谁离0.5近，选择谁分。
min_diff = 100
for var_name in current_node.branch_var_list:
if (abs(current_node.x_sol[var_name] - 0.5) < min_diff):
branch_var_name = var_name
min_diff = abs(current_node.x_sol[var_name] - 0.5)
print(var_name, ' = ', current_node.x_sol[branch_var_name])当然一般意义上，有三种搜索策略（具体的搜索方式对应着后续queue这个数据结构）：
a) 广度优先Breadth-First：也叫地毯式搜索。Breadth-first search (BFS)，就是横向搜索，先搜索同层的节点。再一层一层往下。这种搜索可以用FIFO queue实现。
b) 深度优先Deep-First：就是纵向搜索，先一个分支走到底，再跳到另一个分支走到底。这种搜索可以用LIFO queue也就是栈实现。具体来说，先对某条支进行搜索。对分支定界树的层数（已分支变量的个数）定位节点的深度，优先选择具有最大深度的节点进行分支，也就是单条路一直走到尽头。储存的信息会相对少些。（以下为示例，默认先搜索左节点）
c) 最优优先Best-First：启发式搜索。先对下界最小的节点进行分支，那么它对应的IP问题取得更好上界的可能性就更大。好处在于存储的节点个数最小，但是选择节点的方式是“跳跃式”的，需要储存的信息很多。其基于广度优先搜索算法，不同点是其依赖于估价函数对将要遍历的节点进行估价，选择代价小的节点进行遍历，直到找到目标点为止。这种搜索可以用优先队列priority queue来实现。
2.4 求整数可行解的方法：
比如设计出合理的启发式算法，如贪婪法；其它启发式或元启发式算法；然后将启发式的解通过callback函数推送给gurobi。也能够在比较和剪枝的过程中剪掉一部分枝，也能大大提高求解效率。
3.一般的分支定界方法
一般的非线性混合整数规划（MIP），比如：
其中，f，g_{i}，和h_{k}是n维实数集中的实值函数，是一个整数集合。
一般的求解框架为：
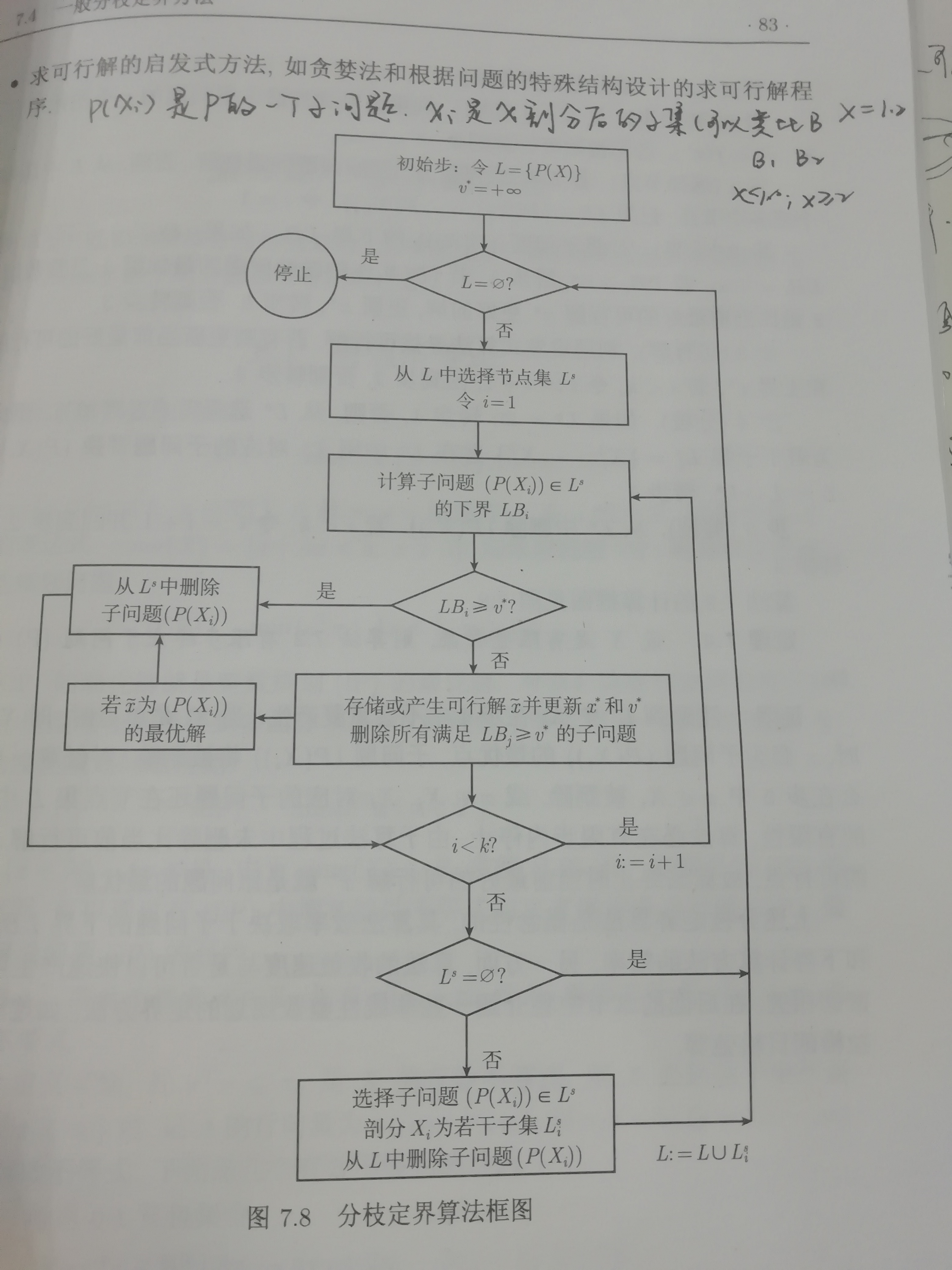
对问题定界的方法：比如凸整数规划问题的连续松弛、线性下逼近方法、可分离整数规划的拉格朗日松弛和二次0-1规划的半正定（SDP）松弛算法等等。
还有设计求可行解的启发式算法，如贪婪法和根据问题的特殊结构设计的求可行解程序。
分支定界算法框架的具体步骤为：
L记为分支定界树中存储的节点（子问题）的集合。所以会涉及到添入（增加节点）和删除（剪枝）。
4.编程关键
在实际编程的时候，
branch分支操作比较简单，可以通过添加约束来实现。但是branch的策略，比如选择深度，广度，还是最优，还是最基础的靠近0.5等策略需要斟酌确定，很可能需要反复推演对比。
会利用到ub=min{f(整数可行解)}，lb=min{f(非整数可行解)}。这点很好用，因此我们需要标注每一个节点（即子问题）的上下界情况。对于IP问题，该点的上下界即本身obj；不是整数解即小数解，上界=全局上界，下界=本身obj。同时我们需要对比每个点的上下界与全局上下界的关系，判断对该点进行剪支，或是进行更新全局上下界的操作。
终止条件通常有两个，一个是所有的节点探测完毕，我们通常会用Queue来标注当前需要探测的节点；另一个是上下界相等或是相距，也可以终止。
通常最好的整数解我们标记为incumbent_node，该点即是gurobi求解信息的incumbent那一列，也是我们最终输出的整数解。其实它的本质就是min{所有的整数可行解}（其实在实际操作中只需要对比（该点的上界<全局上界）否即可，因为全局上界是不断更新的，存储的就是先前最好的整数解）。
1. Using a heuristic, find a solution xh to the optimization problem. Store its value, B = f(x_h). (If no heuristic is available, set B to infinity.) B will denote the best solution found so far, and will be used as an upper bound on candidate solutions.
2. Initialize a queue to hold a partial solution with none of the variables of the problem assigned.
3. Loop until the queue is empty:
3.1. Take a node N off the queue.
3.2. If N represents a single candidate solution x and f(x) < B, then x is the best solution so far. Record it and set B ← f(x).
3.3. Else, branch on N to produce new nodes Ni. For each of these:
3.3.1. If bound(N_i) > B, do nothing; since the lower bound on this node is greater than the upper bound of the problem, it will never lead to the optimal solution, and can be discarded. 3.3.2. Else, store Ni on the queue.
编程的基本思路是：
（1）首先将原模型A松弛为B模型，先copy原模型，再relax即可。
（2）计算该点的解，更新全局上下界信息。上界=inf，下界即该点的解。把该点放在Quene队列中。
（3）判断终止条件，若满足，终止输出；若不满足，继续下述步骤。
（4）从Quene中拿出节点进行求解，若求解出不可行解，剪断该支（不可行剪支）；若求解出的是最优解，那么继续下述步骤。
（5）判断该解是否整数解：若是整数解，更新当前节点的上下界；假如该点是当前最好的整数解，即比较当前整数解的obj<全局上界否，若成立，标记该点为incumbent_node，同时更新全局上界；同时剪断该支（最优性剪支）并返回（3）。若不是整数解，即小数解，那么执行下述步骤。
（6）更新该点的上下界信息，即下界=当前节点的信息，上界=全局上界；同时对比该点的解是否>全局上界，若是，剪断该支（边界剪支）；若并没超，那么该点可以继续执行分支branch操作。
（7）branch操作，按照分支策略选择需要分支的变量或者变量集合；然后将当前节点复制两个，分别添加不同的整数约束（也可以添加边界约束）；然后放在Quene队列中。
（8）遍历Quene队列的模型，看是否有更好的下界，即下界提升否，然后返回到（3）。
现在用在大规模求解IP和MIP的精确算法，比如branch and price和branch and cut算法都是基于分支定界算法框架而设计的。
比如branch and price算法，是在基本的branch and bound的基础上，在求解子节点松弛问题的时候采用列生成的方法，一列一列的添加变量，让问题规模从小变大，而别的都没变。原始的基础的branch and bound中子节点松弛问题的求解直接采用的是单纯形法或内点法，但是对于大规模问题，变量数目是很多的（而一列一列添加可以避免变量数目特别多求解困难的情况）。但并不是说每一个节点每一次都完完整整调用一次column generation，重新构建一次RMP再求解。分支以后子节点的RMP可以直接将父节点的RMP挪过来，只不过由于加了分支约束，此时RMP需要重新添加column，再次求解以便得到最优。
而子节点的RMP重新添加column，再次求解的过程就是节点的bound操作了。那么，将以上的元素综合起来，就形成了我们的branch and price算法。
再比如branch and cut算法，是在基本branch and bound的基础上，在求解子节点松弛问题的时候添加cut，再次判断该点的上下界看是否要分支或者剪支。步骤肯定要比branch and bound要少。
五大常用算法之分支定界法_逍遥天扬的博客-CSDN博客_分支定界法有哪些
干货 | 10分钟掌握branch and cut（分支剪界）算法原理附带C++求解TSP问题代码_infinitor的博客-CSDN博客
干货 | 10分钟带你全面掌握branch and bound（分支定界）算法-概念篇 - 短短的路走走停停 - 博客园 (cnblogs.com)
914
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
