对于标准正态分布,其形式特别友好,而计算四次方数学期望,积分明显是最简单粗暴的方式,网上很多证明过程太过简陋,所以我就自己去尝试着证明了一下,因为是不可积函数,中间需要极坐标转换,证明过程如下,才疏学浅,如有疑问,欢迎留言:



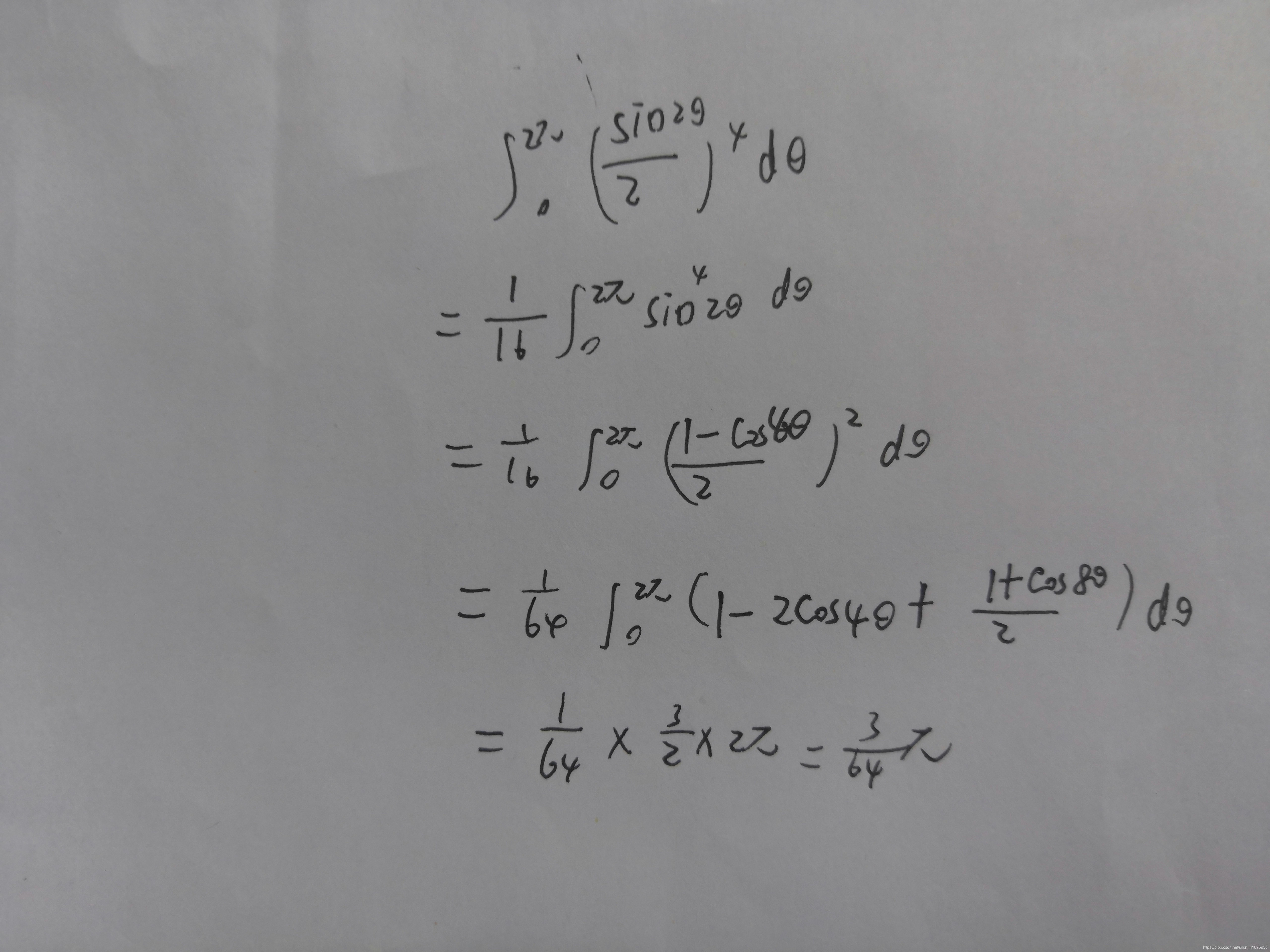

至此,证明完毕,字很潦草,因为证得太急,但是应该不影响,看完前两张图应该就能会证了,后面没有什么技巧性可言。
标准正态分布的E(X^4)积分求解
最新推荐文章于 2023-04-24 19:22:03 发布
对于标准正态分布,其形式特别友好,而计算四次方数学期望,积分明显是最简单粗暴的方式,网上很多证明过程太过简陋,所以我就自己去尝试着证明了一下,因为是不可积函数,中间需要极坐标转换,证明过程如下,才疏学浅,如有疑问,欢迎留言:



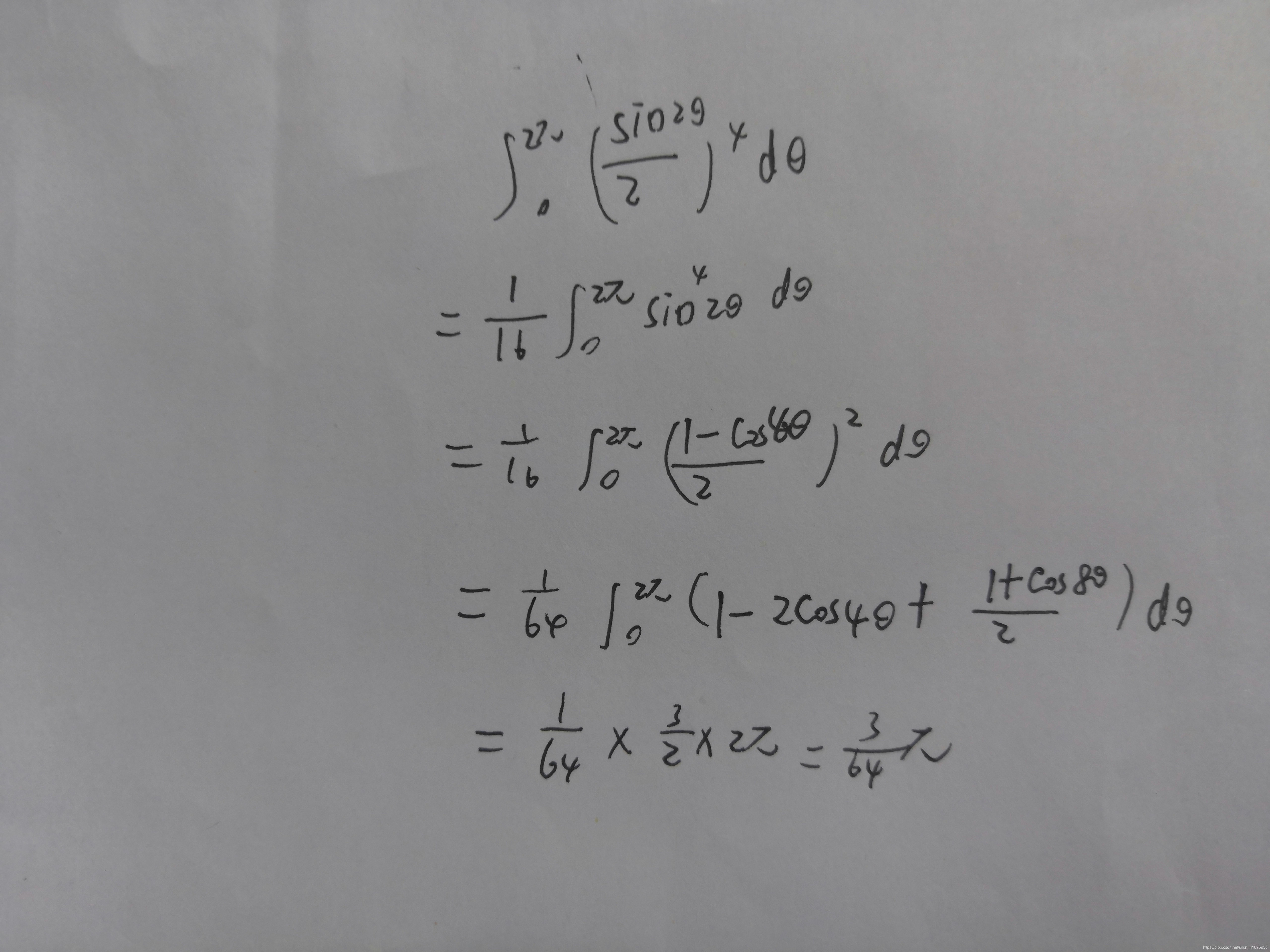

至此,证明完毕,字很潦草,因为证得太急,但是应该不影响,看完前两张图应该就能会证了,后面没有什么技巧性可言。
 1198
1198
 2244
2244
 2783
2783
 3694
3694
 4万+
4万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


