GRPO原理详解
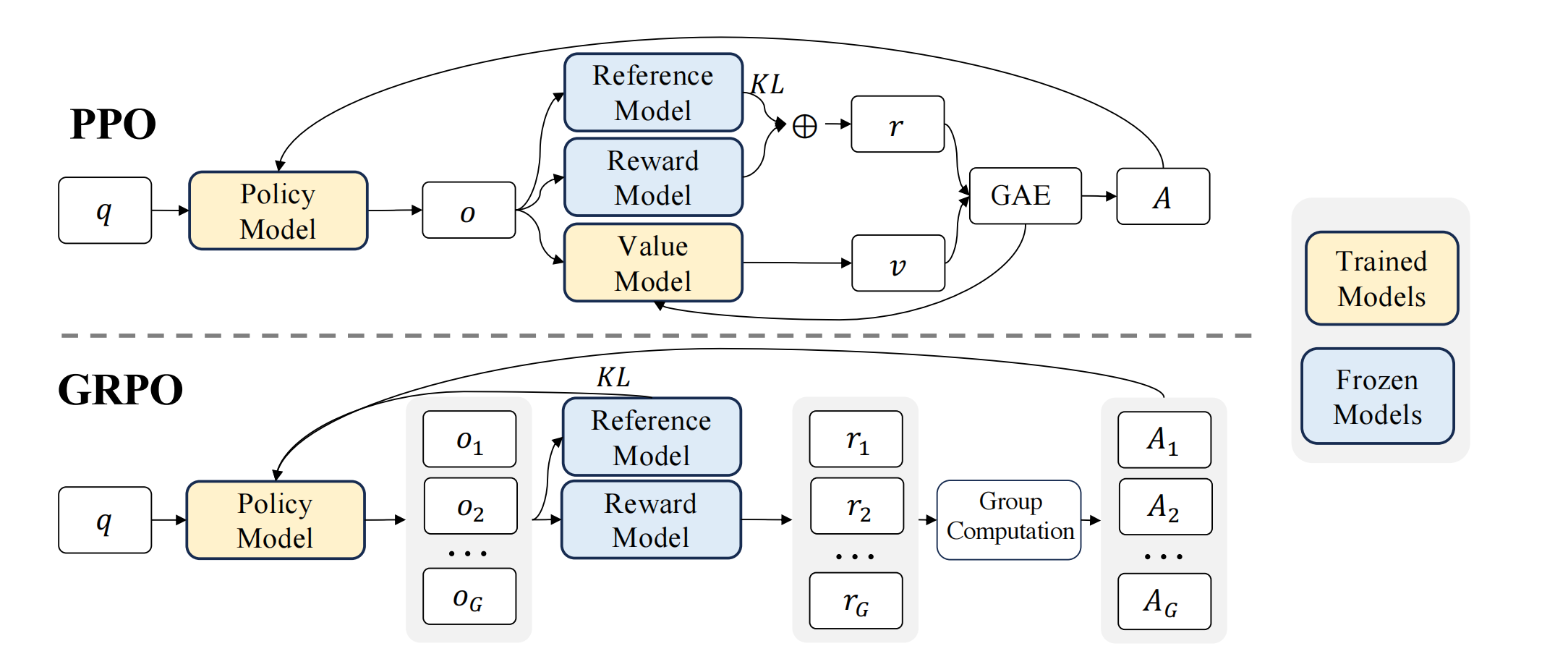
图1 PPO vs GRPO. GRPO处理Value Function(Critic网络),并从组内奖励得分计算基线baseline,大大减少了训练资源。
1. 背景
近端策略优化(Proximal Policy Optimization, PPO)(Schulman等人,2017)是一种actor-critic强化学习算法,被广泛应用于大语言模型(LLM)的强化学习微调阶段。他通过最大化以下损失函数优化LLM。其中πθ\pi_\thetaπθ, πθold\pi_{\theta_{old}}πθold分别时当前策略和旧策略,qqq, ooo是query和对应的πθold\pi_{\theta_{old}}πθold生成的response。AtA_tAt是广义优势估计GAE出来的优势,ttt代表response的token index。广义优势估计的计算需要value function,也就是Critic网络,通常Critic网络是和Policy网络大小一个量级,带来了很大的内存和计算开销。(也有省略Critic的蒙特卡洛PPO,但是效果不如Actor-Critic的PPO)
此外,在强化学习(RL)训练过程中,价值函数会被视为基线(baseline),用于在计算优势函数(advantage)时降低方差。然而,在大型语言模型(LLM)的场景中,通常只有最后一个标记(token)会被奖励模型分配一个奖励分数,这可能导致训练一个能在每个标记级别都保持准确的价值函数变得更为复杂。
JPPO(θ)=E[q∼P(Q),o∼πθold(O∣q)]1∣o∣∑t=1∣o∣min[πθ(ot∣q,o<t)πθold(ot∣q,o<t)At,clip(πθ(ot∣q,o<t)πθold(ot∣q,o<t),1−ϵ,1+ϵ)At]
\mathcal{J}_{PPO}(\theta) = \mathbb{E}[q\sim P(Q), o \sim \pi_{\theta_{old}}(O|q)]\frac{1}{|o|}\sum_{t=1}^{|o|}min\left[ \frac{\pi_\theta (o_t|q, o_{<t})}{\pi_{\theta_{old}}(o_t|q, o_{<t})}A_t, clip\left( \frac{\pi_\theta(o_t|q, o_{<t})}{\pi_{\theta_{old}}(o_t|q, o_{<t})}, 1-\epsilon, 1+\epsilon\right)A_t \right]
JPPO(θ)=E[q∼P(Q),o∼πθold(O∣q)]∣o∣1t=1∑∣o∣min[πθold(ot∣q,o<t)πθ(ot∣q,o<t)At,clip(πθold(ot∣q,o<t)πθ(ot∣q,o<t),1−ϵ,1+ϵ)At]
标准方法是在每个标记的奖励中加入来自参考模型的逐标记KL散度惩罚。因此PPO的奖励模型包含两部分,第一部分是reward per token,另一部分是KL(πθ,πref)KL(\pi_\theta, \pi_{ref})KL(πθ,πref)散度。一般情况下,rφ(q,o≤t)=0 if t<T else Rr_{\varphi}(q, o_{\leq t})= 0 \ if\ t<T\ else\ Rrφ(q,o≤t)=0 if t<T else R。即当t<Tt<Tt<T时,奖励是负的KL散度,当t=Tt=Tt=T(最后一个token)时,奖励是R−KLR-KLR−KL (稀疏奖励).
rt=rφ(q,o≤t)−βlogπθ(ot∣q,o<t)πref(ot∣q,o<t) r_t = r_{\varphi}(q, o_{\leq t}) - \beta \log \frac{\pi_{\theta}(o_t | q, o_{<t})}{\pi_{ref}(o_t | q, o_{<t})} rt=rφ(q,o≤t)−βlogπref(ot∣q,o<t)πθ(ot∣q,o<t)
2. GRPO损失函数
为了解决PPO的问题,如图1所示,Deepseek提出了组相对策略优化(Group Relative Policy Optimization, GRPO)。该方法无需像PPO那样额外进行价值函数近似,而是以针对同一问题生成的多个采样输出的平均奖励作为基线。具体而言,对于每个prompt qqq,GRPO从旧策略πθold\pi_{\theta_{old}}πθold中采样一组输出{oi,o2,⋯ ,oG}\{o_i,o_2,\cdots,o_G\}{oi,o2,⋯,oG},并通过最大化以下目标函数优化策略模型。其中Ai,t^\hat{A_{i,t}}Ai,t^是仅基于各小组内部输出的相对奖励计算的优势值。
GRPO采用群体相对的方式来计算优势函数,这与奖励模型的比较性质非常契合,因为奖励模型通常是在同一问题不同输出间的对比数据集上进行训练的。此外值得注意的是,GRPO并非在奖励中添加KL惩罚项,而是通过直接在损失函数中加入训练策略与参考策略之间的KL散度进行正则化,这种设计避免了复杂化优势函数A^i,t\hat{A}_{i,t}A^i,t的计算过程。
JGRPO(θ)=E[q∼𝑃(𝑄),{oi}i=1𝐺∼πθold(𝑂∣q)]1𝐺∑i=1𝐺1∣oi∣∑t=1∣oi∣[min(πθ(oi,t∣q,oi,<t)πθold(oi,t∣q,oi,<t)A^i,t,clip(πθ(oi,t∣q,oi,<t)πθold(oi,t∣q,oi,<t),1−ϵ,1+ϵ)A^i,t)−βDKL(πθ∥πref)] J_{GRPO}(\theta) = \mathbb{E}\left[q \sim 𝑃(𝑄), \{o_i\}_{i=1}^𝐺 \sim \pi_{\theta_{old}}(𝑂|q)\right] \frac{1}{𝐺} \sum_{i=1}^𝐺 \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left[ \min\left( \frac{\pi_\theta(o_{i,t}|q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q, o_{i,<t})} \hat{A}_{i,t}, \text{clip}\left( \frac{\pi_\theta(o_{i,t}|q, o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q, o_{i,<t})}, 1−\epsilon, 1+\epsilon \right) \hat{A}_{i,t} \right) − \beta D_{KL}(\pi_\theta \| \pi_{ref}) \right] JGRPO(θ)=E[q∼P(Q),{oi}i=1G∼πθold(O∣q)]G1i=1∑G∣oi∣1t=1∑∣oi∣[min(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t)A^i,t,clip(πθold(oi,t∣q,oi,<t)πθ(oi,t∣q,oi,<t),1−ϵ,1+ϵ)A^i,t)−βDKL(πθ∥πref)]
3. GRPO代码
3.1 伪代码

- GRPO的优势是在token级别上计算的
- GRPO同时维护ref,old,current三个策略,其中ref和current计算KL散度,old采样G个sample计算组相对策略奖励,current进行优化
- GRPO的ref策略也会不断使用最新的current策略迭代,因此当训练足够多epoch时,current策略可能离SFT比较远了,即使有KL约束。所以DeepSeek强化学习训练足够充分时可能会对生成语句通顺度、多语言一致性能力有所退化,DeepSeek在强化学习之后再次进行SFT微调,模型reasoning和生成能力都有较好的提升。
3.2 torch代码demo
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
import copy
import random
from collections import deque
class GRPODataset(Dataset):
"""处理提示文本的数据集"""
def __init__(self, prompts, tokenizer, max_length=128):
self.tokenizer = tokenizer
self.encodings = tokenizer(
prompts,
max_length=max_length,
padding='max_length',
truncation=True,
return_tensors='pt'
)
def __len__(self):
return self.encodings.input_ids.size(0)
def __getitem__(self, idx):
return {
'input_ids': self.encodings.input_ids[idx],
'attention_mask': self.encodings.attention_mask[idx]
}
class GRPOTrainer:
def __init__(self, policy_model, ref_model, reward_model, tokenizer,
I=10, M=5, mu=3, G=4,
batch_size=32, clip_epsilon=0.2, beta=0.1,
max_seq_len=128, replay_ratio=0.1):
"""
GRPO算法训练器
参数说明:
- I: 外层总迭代次数(epoch数)
- M: 每个epoch内的训练步数
- mu: 每个训练步的策略更新次数
- G: 每组生成的响应数量
- replay_ratio: 历史数据回放比例
"""
# 模型组件初始化
self.policy = policy_model.to('cuda') # 当前策略模型
self.ref_model = ref_model.to('cuda') # 参考模型(用于KL计算)
self.old_policy = copy.deepcopy(policy_model) # 旧策略(用于轨迹采样)
self.reward_model = reward_model # 奖励模型
self.tokenizer = tokenizer
# 超参数设置
self.I = I
self.M = M
self.mu = mu
self.G = G
self.batch_size = batch_size
self.clip_eps = clip_epsilon
self.beta = beta
self.max_seq_len = max_seq_len
# 优化器
self.optimizer = torch.optim.AdamW(self.policy.parameters(), lr=1e-5)
# 历史数据管理
self.replay_buffer = deque(maxlen=10000) # 历史轨迹存储
self.replay_ratio = replay_ratio
def train(self, dataset):
"""外层主训练循环"""
for epoch in range(self.I):
# 阶段1: 同步参考模型
self._sync_ref_model()
# 阶段2: 执行M个训练步
for _ in range(self.M):
# 采样数据批次
batch = self._sample_batch(dataset)
# 执行单步训练
self._train_step(batch)
def _train_step(self, batch):
"""单训练步核心逻辑"""
# 阶段1: 冻结旧策略用于轨迹采样
self.old_policy.load_state_dict(self.policy.state_dict())
# 阶段2: 生成响应组
responses, old_logprobs = self._generate_responses(batch)
# 阶段3: 奖励计算
rewards = self.reward_model(responses) # (B, G)
advantages = self._compute_advantages(rewards) # (B, G)
# 阶段4: μ次策略优化
for _ in range(self.mu):
loss = self._update_policy(responses, old_logprobs, advantages)
# 阶段5: 奖励模型更新(含历史回放)
self._update_reward_model(responses, rewards)
def _generate_responses(self, prompts):
"""使用旧策略生成响应组"""
self.old_policy.eval()
batch_size = prompts['input_ids'].size(0)
all_tokens, all_logprobs = [], []
with torch.no_grad():
# 为每个prompt生成G个响应
for i in range(batch_size):
prompt = {
'input_ids': prompts['input_ids'][i:i+1].to('cuda'),
'attention_mask': prompts['attention_mask'][i:i+1].to('cuda')
}
# 生成响应
outputs = self.old_policy.generate(
**prompt,
max_length=self.max_seq_len,
num_return_sequences=self.G,
output_scores=True,
return_dict_in_generate=True
)
# 提取生成内容
tokens = outputs.sequences[:, prompt['input_ids'].size(1):] # 去除prompt
logprobs = self._compute_seq_logprobs(outputs.scores, tokens)
all_tokens.append(tokens)
all_logprobs.append(logprobs)
return torch.stack(all_tokens), torch.stack(all_logprobs) # (B, G, L), (B, G)
def _compute_seq_logprobs(self, scores, tokens):
"""计算序列对数概率"""
logprobs = []
for step, step_scores in enumerate(scores):
logp = F.log_softmax(step_scores, dim=-1)
token = tokens[:, step]
logprobs.append(logp.gather(-1, token.unsqueeze(-1)).squeeze())
return torch.stack(logprobs, dim=1).sum(dim=1) # (G,) per sequence
def _compute_advantages(self, rewards):
"""组内标准化优势计算"""
mean = rewards.mean(dim=1, keepdim=True)
std = rewards.std(dim=1, keepdim=True) + 1e-8
return (rewards - mean) / std # (B, G)
def _update_policy(self, responses, old_logprobs, advantages):
"""策略模型更新"""
# 转换数据维度
B, G, L = responses.shape
flat_responses = responses.view(B*G, L)
# 计算新策略概率
new_logprobs = self.policy.log_prob(flat_responses).view(B, G) # (B, G)
ratio = torch.exp(new_logprobs - old_logprobs)
# PPO裁剪目标
clipped_ratio = torch.clamp(ratio, 1-self.clip_eps, 1+self.clip_eps)
policy_loss = -torch.min(ratio*advantages, clipped_ratio*advantages).mean()
# KL散度惩罚项(当前策略 vs 参考模型)
kl_penalty = self._compute_kl(flat_responses)
# 综合损失
total_loss = policy_loss + self.beta * kl_penalty
# 反向传播
self.optimizer.zero_grad()
total_loss.backward()
torch.nn.utils.clip_grad_norm_(self.policy.parameters(), 1.0)
self.optimizer.step()
return total_loss.item()
def _compute_kl(self, responses):
"""计算当前策略与参考模型的KL散度"""
# 参考模型输出
with torch.no_grad():
ref_logits = self.ref_model(responses).logits # (B*G, L, V)
# 当前策略输出
policy_logits = self.policy(responses).logits
# 逐token计算
kl = F.kl_div(
F.log_softmax(policy_logits, dim=-1),
F.log_softmax(ref_logits, dim=-1),
log_target=True,
reduction='batchmean'
)
return kl
def _update_reward_model(self, responses, rewards):
"""带历史回放的奖励模型更新"""
# 转换数据格式
B, G, L = responses.shape
flat_res = responses.view(B*G, L).cpu().numpy()
flat_rew = rewards.view(B*G).cpu().numpy()
current_data = list(zip(flat_res, flat_rew))
# 历史数据采样
replay_samples = []
if self.replay_buffer:
replay_size = int(len(current_data)*self.replay_ratio)
replay_samples = random.sample(self.replay_buffer, replay_size)
# 组合训练数据
train_data = current_data + replay_samples
# 更新奖励模型
self.reward_model.train_on_data(train_data)
# 更新历史缓存
self.replay_buffer.extend(current_data)
def _sync_ref_model(self):
"""同步参考模型参数"""
self.ref_model.load_state_dict(self.policy.state_dict())
def _sample_batch(self, dataset):
"""动态批次采样"""
dataloader = DataLoader(
dataset,
batch_size=self.batch_size,
shuffle=True,
collate_fn=lambda b: {
'input_ids': torch.stack([x['input_ids'] for x in b]),
'attention_mask': torch.stack([x['attention_mask'] for x in b])
}
)
return next(iter(dataloader))
# 使用示例
if __name__ == "__main__":
from transformers import AutoTokenizer, AutoModelForCausalLM
# 初始化组件
tokenizer = AutoTokenizer.from_pretrained("gpt2")
policy_model = AutoModelForCausalLM.from_pretrained("gpt2")
ref_model = AutoModelForCausalLM.from_pretrained("gpt2")
# 定义简单奖励模型(实际需自定义)
class RewardModel(nn.Module):
def __init__(self):
super().__init__()
self.scorer = nn.Linear(768, 1)
def forward(self, input_ids):
# 实际需要实现奖励逻辑
return torch.randn(input_ids.size(0))
# 创建训练器
trainer = GRPOTrainer(
policy_model=policy_model,
ref_model=ref_model,
reward_model=RewardModel(),
tokenizer=tokenizer,
batch_size=4,
G=2
)
# 模拟训练
prompts = ["Explain quantum physics in", "Write a poem about"]*100
dataset = GRPODataset(prompts, tokenizer)
trainer.train(dataset)
4. 总结
- GRPO相比标准RLHF-PPO,采用了组内相对奖励作为优势函数,符合奖励函数的定义
- GRPO省略了Critic网络,节省了计算资源,同时避免了PPO采用Critic网络在稀疏奖励下学习高质量价值函数的问题
- GRPO将KL散度直接作为正则项优化,简化了优势函数的计算
- RLHF-PPO也可以优化省略Critic网络,比如采用蒙特卡洛方法,方法不固定,重要的是思想
参考文献:
DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models https://arxiv.org/abs/2402.03300




























 902
902

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










