Basic Concept and Theorem of Statistical Learning(一)

I. Preface

  为了学习统计学习基础课程，需要将本科阶段的概率论与数理统计的基本概念和思想复习。这里主要就是复习这本书的记录。这次的复习更加注重其中的统计思想和其应用。

II. Catalogue

1. 随机事件、概率以及基本统计概念

2. 随机变量的数字特征

3. 常见的分布及其数字特征

4. 极限定理

5. 数理统计基本概念

6. 参数估计

7. 假设检验

III. Content

一. 随机事件、概率以及基本统计概念

1. 随机事件
当事件的发生不是直接能够利用某些确定性理论来确定事件发生与不发生。
2. 概率
1) 古典概率
如果事件的发生可能只有两种，那么称这种事件为古典概型。
2) 几何概率
通过几何建模的方式，利用面积的比例来进行概率计算。这种概型当然只适合用于一些分布情况均匀的概型。
3) 概率的频率定义
频率作为概率的随机事件的体现；当实验的次数足够大的时候频率会不断的接近概率。
4) 主观概率
对于那些无法进行重复实验的事件，比如明天的天气是晴朗的概率等等。而利用合理的信念的测度进行概率的定义。
5) 条件概率和独立性
独立同分布 IID(Independent identically distribution) 
6) 全概率公式
7) 贝叶斯概率模型
贝叶斯概率模型是基于条件概率和全概率公式提出的。主要是提出了基于先验概率来进行后验概率的计算和估计。
3. 随机变量、分布函数和概率密度函数
1) 随机变量
随机变量是对随机事件中某一个方向的研究体现，例如掷硬币中的正面的次数、反面的次数等等。
2) CDF
Cumulative distribution function，也就是书上所讲的分布函数。
这是描述一个随机变量分布的一个累积特征。直观定义上就是随机变量小于某一个数值的概率大小。
3) PDF
Probability distribution function，也就是书上的概率密度函数。是分布的”单位”概率，也就是概率密度。
4) PMF
Probability mass function，是离散概率分布的概率质量函数 P(X=k)

二. 随机变量的数字特征

1. 一维随机变量的数字特征
1) 期望(Expectation)
直观意义上说数学期望反映一个随机变量分布的平均情况。
数学期望的一些性质
2) 方差(Variance) 标准差(Standard Variance)
方差在直观意义上就是反应一个随机变量分布的波动性，也就是其稳定性的表现。
标准方差是由于方差的单位与随机变量的单位不一致因此通过开平方将两者弄成一致！
方差的一些性质
3) 中位(Median)
当随机变量=x是发生的概率为0.5则x称为其中位. 推展开来还有分位数.
4) 矩(Moment)
Kth Origin Moment  K阶原点矩 X的k次方的期望. First Origin Moment -- 数学期望
Kth Central Moment k阶中心矩X-E(X)的K次方的期望
矩是很重要的数字特征之一，在参数估计中的点估计常常利用K阶矩进行参数估计. Method of Moment.

2. 二维随机变量
1) 协方差
其定义E((E(x)-x)(E(y)-y)).
2) 相关系数
由于协方差的大小还由两个随机变量的大小决定，因此对于两者之间的联系的描述没有那么强烈。因此引入了相关系数来表示.
定义
这里定义的相关系数事实上是线性相关的大小，当两个随机变量的相关系数等于1时候，两者线性相关。等于0时则不相关。
柯西-施瓦茨不等式; 事实上就是证明上述所说的线性相关的本质。
两个随机变量不相关并不能推出两个随机变量互相独立; 但是有如下的性质:
Cov(x, y) =0
E(XY)=E(X) * E(Y)
D(XY) = D(X) * D(Y)
正态分布如果不相关则可以推出独立！

三. 常见的分布以及数字特征

Reference: http://www.pyrtvu.cn/jinjishuxue/lesson/ch08/0802.html

1. 连续型随机变量(Continuous)
1) 高斯分布/正太分布(Normal Distribution)
概率密度函数:
期望: u
标准差:
标准正态分布 --- 正态分布的标准化
高斯分布十分重要，因为一则高斯分布有很多研究成果可以利用，有很多特性。二则，很多分布可以用高斯分布来进行逼近。
应用: 在测量误差、人的身高、工厂产品的尺寸等问题; 通常对于一个随机变量有很多独立的因素共同决定，则这个随机变量通常符合高斯分布.
2) 均匀分布(Uniform Distribution)
概率密度函数;
期望: (a + b)/2
方差: (b − a)²/12
应用: 几何概率中就是基于这种均匀的分布特点.
3) 指数分布(Exponential Distribution)
http://zh.wikipedia.org/zh/%E6%8C%87%E6%95%B0%E5%88%86%E5%B8%83


无记忆性(Memoryless Property), 这表示如果一个随机变量呈指数分布，它的条件概率遵循：

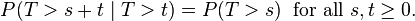
应用：在排队理论和可靠性理论中有重要的应用，通常的一些"寿命"模型可以用这个分布来模拟。

4) 伽马分布(Gamma Distribution)
其中Gamma Function在组合数学和概率论中很重要
Mark! ---- 这个分布、对应的一个分布类以及伽马函数等需要复习！
2. 离散型随机变量分布(Discrete)
1) 两点分布(Bernouli Distribution)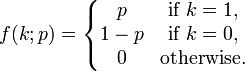

E(X) = p
V(X) = p(1-p)
常见的掷硬币的实验就是Bernouli Distribution
2) 二项分布(Binomial Distribution)
是Bernouli分布的拓展.
http://zh.wikipedia.org/zh-cn/%E4%BA%8C%E9%A1%B9%E5%88%86%E5%B8%83

E(X) = np
V(X) = np(1-p)
问题: 当N很大的时候f(X)变得很难求解，此时使用泊松定理来解决.
3) 泊松分布(Poisson Distribution)
http://en.wikipedia.org/wiki/Poisson_distribution

E(X) = λ
V(X) = λ
应用：当某一个容器或者时间段可以划分成n小块，n趋向于无穷大，每一块中事件发生的概率都很小.
4) 几何分布(Geometric distribution)和超几何分布（Hypergeometric distribution ）
几何分布（Geometric distribution）是离散型概率分布。其中一种定义为：在第n次伯努利试验，才得到第一次成功的机率。详细的说，是：n次伯努利试验，前n-1次皆失败，第n次才成功的概率。


超几何分布; 产品抽样检查中经常遇到一类实际问题，假定在N件产品中有M件不合格品，即不合格率p=M/N.在产品中随机抽n件做检查，发现X件是不合格品，可知X的概率函数为P(X=k)=C(k,M)*C(n-k,N-M)/C(n,N),k=max{0,n-N+M},...,min{n,M}通常称这个随机变量X服从超几何分布。这种抽样检查方法等于无放回抽样。数学上不难证明，N--无穷，limC(k,M)*C(n-k,N-M)/C(M,N)=B(n,p) (二项分布) 因此，在实际应用时，只要N>=10n，可用二项分布近似描述不合格品个数。
超几何分布的均值：
对X~H(n，M，N)，E(x)=nM/N
超几何分布的方差：
对X~H(n，M，N)，D(X)=nM(N-M)(N-n)/[(N^2)(N-1)]