一、特征值和特征向量
1、计算 λ 和 ξ
A ξ = λ ξ
| A - λE | = 0
(A - λE 化为行最简)
取 λ1 时,A X = 0 ⇒ ξ1 =
取 λ2 时,A X = 0 ⇒ ξ2 =

2、 λ 和 ξ 线性关系
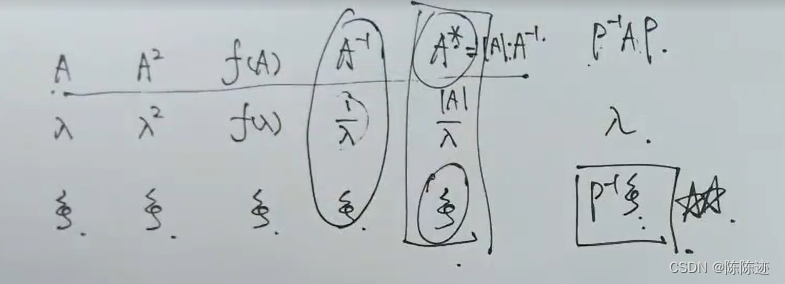
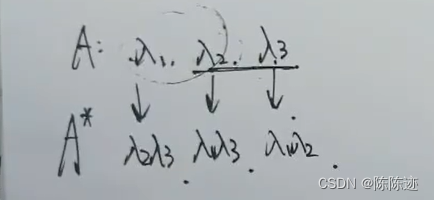
3、秩一方阵
二、矩阵相似
若
=
,则 |A - λE| = 0。
若普通矩阵 A、B 相似,则 r(A) = r(B)、tr(A) = tr(B)、 |A| = |B|、|A - λE| = |B - λE| 即 A 和 B 的 特征值 相同。
=
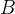
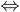
和
相似。

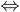

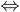
和
相似。
若两矩阵相似,则它们的秩相等。如果秩不等,则不相似。
三、
Q = (α1,α2,α3)
A Q = Q B
A (α1,α2,α3) =( α1+α2+α3,2α2+α3,2α2+3α3 )
所以
对 B 进行| B-λE | = 0,得到 B 的特征值,
因为 A 和 B 相似,所以B的特征值等于A的特征值。
由 (B-λE)X=0 得 B 的特征向量 α ,
因为
的特征向量为 α ,所以 A 的特征向量为 Q α。
矩阵 P 由 A 的特征向量组合得到。
四、谱分解定理
题眼:A为实对称矩阵,求A
五、二次型 → 标准型
正交变换法


配方法










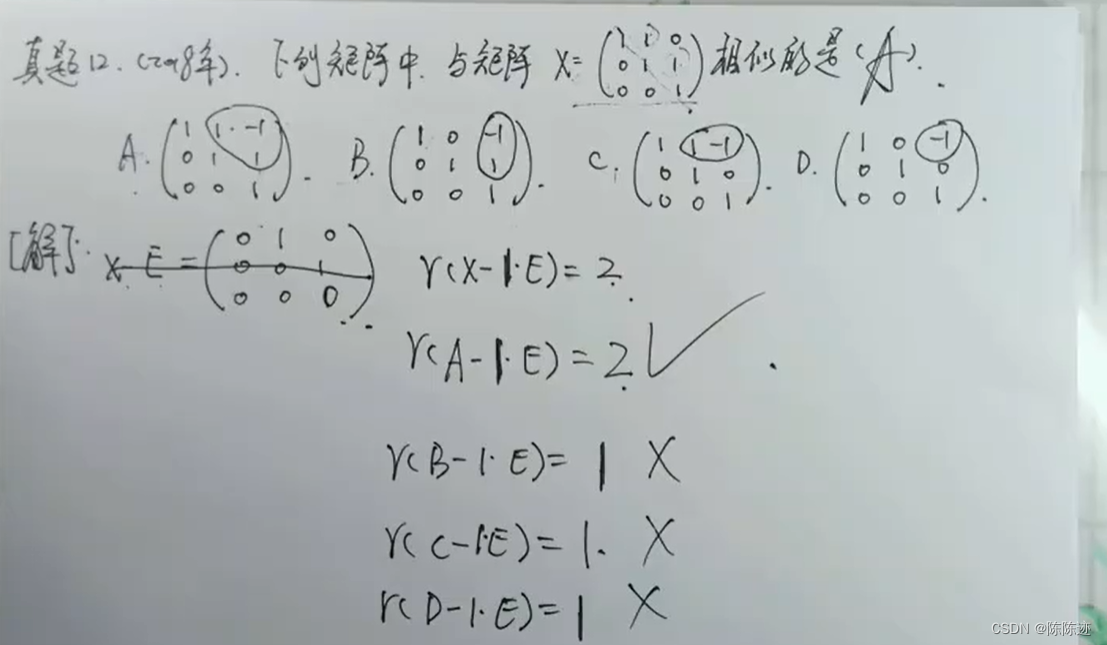



















 11万+
11万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








