题意:给定一个集合A{1…n},计算集合的美丽值(mod 258280327):
Mr.Zstu的算法:将集合变成序列,一个序列的美丽值是这个序列所有区间GCD之和,一个集合的美丽值是这个集合所有可能序列的美丽值之和。例如:集合{1,2,3}可以是6种不同的序列:{1,2,3},{1,3,2},{2,1,3},{2,3,1},{3,1,2},{3,2,1}。
Mr.Hdu的算法:对于k(取值为1~n),从集合中选择k个数字,计算它们的GCD。k个数字的美丽值是k*GCD。一个集合的美丽值是所有k个数字的美丽值之和。
题解:
nlogn预处理出1~100000的因子。
nlogn预处理出1~100000的莫比乌斯系数。
对于集合A,求出cnt[i](表示集合中 i 的倍数的个数)
对于ZSTU:
F1[ x ]表示gcd为x的倍数的区间的个数;
f 1[ x ]表示gcd为x的区间的个数;
F[ i ] = sigma(A(cnt[i],j)* (n-j+1)!) (先选出j个元素的排列,然后捆绑法计算总数 )
对于HDU:
F2[ x ]表示gcd为x的倍数的选法的系数;
f 2[ x ]表示gcd为x的选法的系数;
F2[ i ]=sigma(k* c(cnt[i],k))=cnt[i] * (2^(cnt[i]-1))
直接套莫比乌斯反演,计算 f [ ] ,ans=sigma(i * f [ i ])
知识积累: 莫比乌斯反演 链接 http://blog.csdn.net/acdreamers/article/details/8542292
莫比乌斯反演的两种形式:
定理: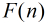
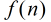
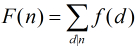
在上面的公式中有一个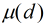
(1)若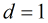
(2)若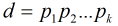
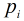
(3)其它情况下
对于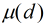
(1)对任意正整数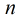
利用该性质,可O(NlogN)的求出1~N的μ值
(2)对任意正整数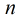
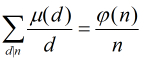
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>
#include <map>
#define clr(x, y) memset(x, y, sizeof x)
using namespace std;
typedef long long LL;
const LL mod=258280327;
const int MAXN=1e5+10;
int mu[MAXN];
int a[MAXN];
int cnt[MAXN];
vector <int> fac[MAXN];
LL po[MAXN];
LL jc[MAXN];
LL F1[MAXN],f1[MAXN];
LL F2[MAXN],f2[MAXN];
int n;
void init()
{
//预处理1~100000的莫比乌斯系数
for(int i=1;i<MAXN;i++)
{
int target= i==1 ? 1:0;
int delta=target-mu[i];
mu[i]=delta;
for(int j=i+i;j<MAXN;j+=i)
mu[j]+=delta;
}
//预处理阶乘和2的幂
jc[0]=jc[1]=1;
po[0]=1; po[1]=2;
for(int i=2;i<MAXN;i++)
{
jc[i]=(jc[i-1]*i)%mod;
po[i]=(po[i-1]*2)%mod;
}
//预处理1~100000的因子
for(int i=1;i<MAXN;i++)
{
fac[i].clear();
}
for(int i=1;i<MAXN;i++)
{
for(int j=i;j<MAXN;j+=i)
{
fac[j].push_back(i);
}
}
}
void cal(int maxn,LL &sum1,LL &sum2)
{
for(int i=1;i<=maxn;i++)
{
F1[i]=0;
LL temp=cnt[i];
for(int j=1;j<=cnt[i];j++)
{
F1[i]=(F1[i]+temp*jc[n-j+1]%mod)%mod;
temp=temp*(cnt[i]-j)%mod;
}
F2[i]=cnt[i]*po[cnt[i]-1]%mod;
}
for(int i=1;i<=maxn;i++)
{
f1[i]=0; f2[i]=0;
for(int j=i;j<=maxn;j+=i)
{
f1[i]=(f1[i]+mu[j/i]*F1[j])%mod;
f2[i]=(f2[i]+mu[j/i]*F2[j])%mod;
}
}
sum1=sum2=0;
for(int i=1;i<=maxn;i++)
{
sum1=(sum1+f1[i]*i)%mod;
sum2=(sum2+f2[i]*i)%mod;
}
sum1=(sum1+mod)%mod;
sum2=(sum2+mod)%mod;
}
int main()
{
init();
while(scanf("%d",&n)!=EOF)
{
memset(cnt,0,sizeof(cnt));
int maxn=0;
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
maxn=max(maxn,a[i]);
for(int j=0;j<fac[a[i]].size();j++)
cnt[fac[a[i]][j]]++;
}
LL sum1,sum2;
cal(maxn,sum1,sum2);
if(sum1>sum2)
printf("Mr. Zstu %I64d\n",sum1);
else if(sum1<sum2)
printf("Mr. Hdu %I64d\n",sum2);
else
printf("Equal %I64d\n",sum2);
}
return 0;
}








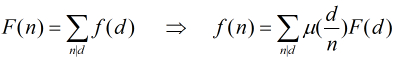

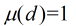
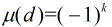
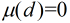
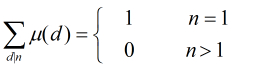














 981
981

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








