直线的黑塞范式（hesse normal form of a line）

再见小菜鸡

于 2024-03-20 20:36:19 发布

阅读量232

点赞数 6

文章标签： matlab python 计算机视觉人工智能数学建模

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/snikerlii/article/details/136886569

版权

直线的黑塞范式是由数学家奥斯卡·黑塞提出，便于表示某点到直线的距离。

一般表达式

黑塞范式的一般表达式为：

$\alpha x+\beta y+\gamma =0$
其中： $\alpha ^{2}+\beta^{2}=1$

或表示为：

$xcos\varphi+ysin\varphi-p=0$

其中角 $\varphi$ 为直线与 $y$ 轴的夹角， $p$ 为直线到原点的距离。

推导过程

下面给出推导过程，

假设有一直线 $l$ ，如图所示：

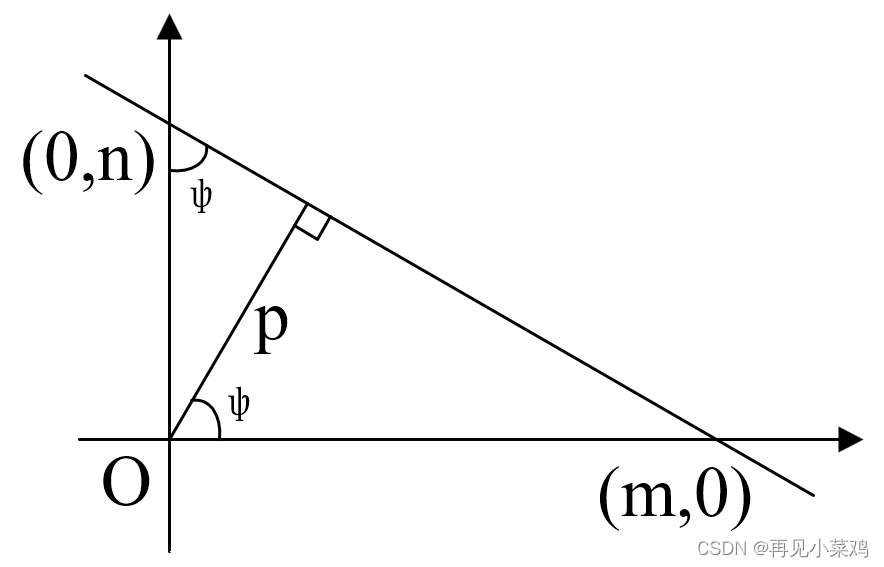
由图可知：

$cos\psi =\frac{p}{m}$

$sin\psi =\frac{p}{n}$

即：

$m=\frac{p}{cos\psi }$

$n=\frac{p}{sin\psi }$

根据直线截距式，可以将直线表示为：

$\frac{x}{m}+\frac{y}{n}=1$

将 $m n$ 代入，即：

$x cos\psi + y sin\psi -p =0$

即：

$\alpha x+\beta y+\gamma =0$

$\alpha =cos\psi$

$\beta =sin\psi$

$\gamma =-p$

与一般式之间的转换

将直线表示的一般式改为：

$\lambda Ax+\lambda By+\lambda C=0$

$\lambda A=cos\psi$

$\lambda B=sin\psi$

即：

$(\lambda A)^{2}+(\lambda B)^{2}=1$

$\lambda^{2}(A^{2}+B^{2})=1$

$\lambda=\pm \frac{1}{\sqrt{A^{2}+B^{2}}}$

即可以将一般式表示为黑塞范式：

$\frac{Ax+By+C}{\pm\sqrt{A^{2}+B^{2}}}=0$

点到直线的距离

若线外有一点 $M(x_{0},y_{0})$ ,求该点到直线的距离：

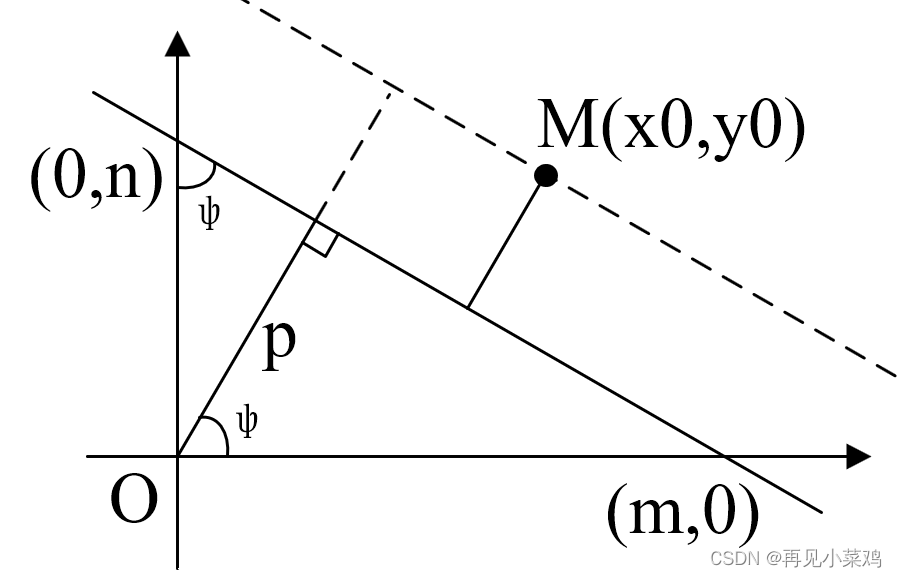
则该点所在平行线与原点的距离为：

$x_{0}cos\psi+y_{0}sin\psi-p_{0}=0$

$p_{0}=x_{0}cos\psi+y_{0}sin\psi$

该点到直线的距离为：

$\Delta p=p_{0}-p=x_{0}cos\psi+y_{0}sin\psi-p$

转化为一般式即：

$\Delta p=\frac{Ax0+By0+C}{\pm\sqrt{A^{2}+B^{2}}}$

再见小菜鸡

关注

6
点赞
踩
5

收藏

觉得还不错? 一键收藏
0
评论
直线的黑塞范式（hesse normal form of a line）

直线的黑塞范式是由数学家奥斯卡·黑塞提出，便于表示某点到直线的距离。
复制链接

扫一扫

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。