Machine Learning 之 Learning

最新推荐文章于 2024-11-06 14:17:31 发布

snow_lyy

最新推荐文章于 2024-11-06 14:17:31 发布

阅读量260

点赞数 1

分类专栏： Machine Learning 文章标签：机器学习算法

本文链接：https://blog.csdn.net/snow_lyy/article/details/75212601

版权

Machine Learning 专栏收录该内容

2 篇文章 0 订阅

订阅专栏

Machine Learning 之 PLA

总结自台大林轩田老师的machine learning 课程：https://www.youtube.com/playlist?list=PLXVfgk9fNX2I7tB6oIINGBmW50rrmFTqf

Learning Model

由银行是否发放信用卡为例引入机器学习模型，如图1所示：

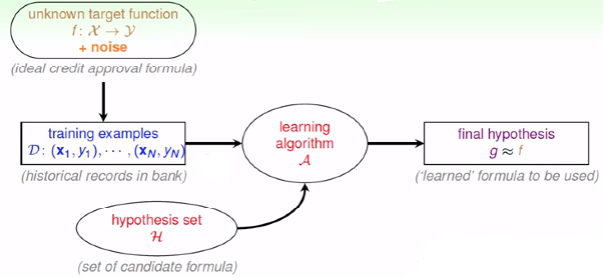
图1：Learning Model

学习的前提有：

输入x与输出y之间存在可以学习的规则f；
在学习之前，我们不知道x与y之间的规则（我之前觉得这是显然的事情，不然还学什么~）
有数据data

所以学习的目标就是通过演算法A选择合适的假设h使得规则g与f尽可能的接近。所以g是演算法从很多规则H中选择出来的，它认为最接近f的规则。依然以银行为例，H中可能是以用户收入大小作为规则，或者以用户年龄、用户职业能作为规则，所以演算法就是种种规则中选择出最优的h作为g。所以整个过程就是： A takes D and H to get g that approximates target f.

Machine Learning and other Fields

Machine Learning VS Data Mining

ML: use data to compute hypothesis g that approximates target f. 可以说目标是很明确的

DM: use ( huge) data to find property that is interesting. 可能仅仅是希望找到数据间的有趣联系

Machine Learning VS Artificial Intelligence

AI: compute something that shows intelligent behavior. 例如chess playing. ML是实现AI的一种方法。

Machine Learning VS Statistics

S: use data to make inference about an unknown process. 统计相对机器学习更注重数学推论，统计的很多方法可以用于实现ML。

Classification: Perceptron Learning Algorithm (PLA)

是否题的学习过程，依然以银行是否发放信用卡为例。Data中每一个用户信息可以包括多方面的特征，如年龄，工龄，收入，职业等。在决定发放信用卡的时候不同的特征我们可以赋予不同的权重。如果银行更关心年收入，那么年收入的权重会大一些，相对而言年龄的权重可能会小一些。在判断是否题的时候，可以利用这些特征*权重的综合与阈值之间的关系来决定是或者否。如图2所示：

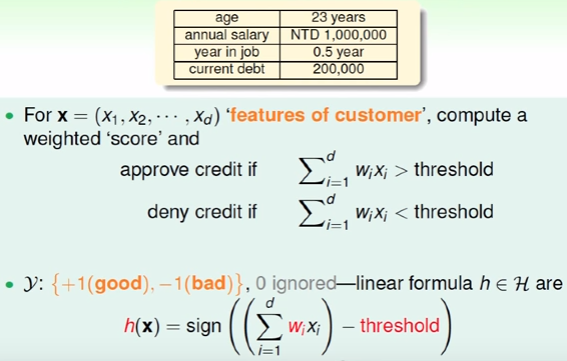
图2：Classification

如图2所示，不同的权重值，不同的threshold就会对应一个 h。为了方便计算，引入x0和w0

图3：Vetor Form of Perceptron Hypothesis

所以我们的演算法从H中选择的g就是将data完美分割为两类：是、否。以2维空间为例，W'x=0就是平面上的一条线。而PLA就是以一个点为起始，画一条线，不断判断（xi,yi）是否分类正确，当发现分类不正确的点时开始修正w，画新的线，再去找不正确的点... 修正的方法如图4所示：

图4：Correction of weight

如果期望值为正，sign(w'x)确是负的，wxcos(angle)说明夹角太大，修正。修正过程到所有data都被h正确分割才会停止。这里就有一个问题：这个演算法会停下来吗？哪些情况下会停下来，哪些时候永远不会停下来？如图5所示，只有线性可分的数据才会存在一条线可以将数据分割。

那么如果data线性可分，演算法PLA会停下来吗？这里依然截图林老师的推导过程，主要思想即：如果停会有一个wf完美分割data，那么应该存在一个wt=wf。这就转化为了衡量两个向量是否接近，衡量两个向量是否接近可以用內积来判断。內积越大可以是向量长度引起的，也可以是角度上越来越接近，所以如果可以证明不是长度引起的，则两个內积越来越大就可以肯定wt与wf越来越接近，最终停止。

图5：內积越来越大

然后只需要证明wt的长度不会增长太快，那么內积越来越大就可以认为是由角度引起的，wt与wf越来越接近。

图6：Not Grow Too Fast

这里的constant我是真的没有推导出来

PLA有个问题就是1.首先我们是假设data是线性可分的，实际上并不知道；2.data中一般是由noisy的，不可能完美分割的情况下我们可以期望找到一个错误最小的w，错误最小的求解过程是NP-hard to solve。解决方法 modify PLA by keeping best weights in pocket. 将更好的w抓在手中。比PLA费时间：a.存一个w，然后计算下一个；b.计算得到w后要遍历所以数据，然后决定哪个w更好。而PLA只需要找到一个错误的点就可以开始修正。

到目前开始林老师课程思想的精髓我应该还是get到了！！开心:-)