Asymmetric Non-local Neural Networks

Asymmetric Non-local Neural Networks

论文：Asymmetric Non-local Neural Networks for Semantic Segmentation,ICCV,2019.

链接：paper

代码：github

本文是在Non-local Neural Networks（cvpr,2018) 这篇论文的基础上改进得来的，non-local block Non-local模块作为语义分割任务中很有用的技术，但因为计算量较大，需要较大的显存开销，这阻碍了non-local network在实际应用中的使用。本文提出了APNB来减少non-local block的计算量和显存开销,AFNB通过提升分割性能增强non-local block的学习能力。我们着重分析这篇论文的改进点。

Revisiting Non-local Block

输入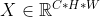

1.经过3个1x1的卷积Query，Key和Value变换之后，分别得到 : ，，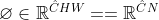

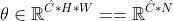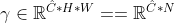
2.计算所有空间位置特征向量的相似度：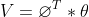

3.归一化：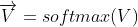

4.根据所有空间位置特征向量的相似度加权求和：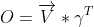

5.新特征经过1*1卷积变换后与原输入特征拼接：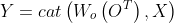

计算复杂度：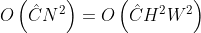

Asymmetric Pyramid Non-local Block(APNB)

Non-local 的计算复杂度主要来自第2步和第4步：

可以看出经N（红色）改变为S，不会改变输出的size。