一道初等平面几何竞赛题的暴力解法

问题

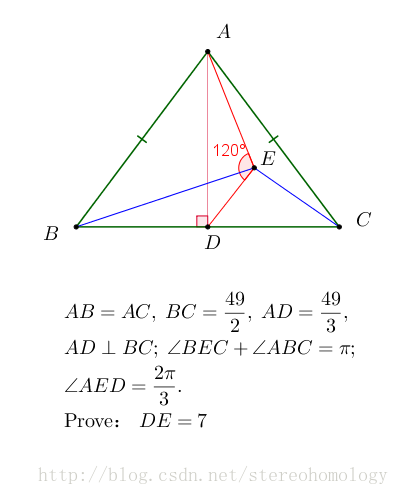
一道初中数学竞赛，平面几何题计算：

这里改成了证明题，反正思路是一样的。

暴力解法

中学的题就应该有中学的解法。但是，看习惯了高等数学的内容之后，更习惯暴力解法。暴力破解的方法是怎样的？

首先，代数方法对很大一部分这类问题都是可以算的；在教学中，可以建议学生，如果其它的几何的解法走不通，不妨尝试代数的、解析的方法。

但是应该注意下面几点，尤其是已经学习了高等数学知识、持有“可以因此俯视甚至藐视任何初等问题”的看法者：
1. 并不是所有初等几何问题都是容易代数化的；
2. 直接代数化并不总能保证所用代数方法不超出初等数学范畴；
3. 代数化之后的代数求解方法也不总能起到简化求解的作用。

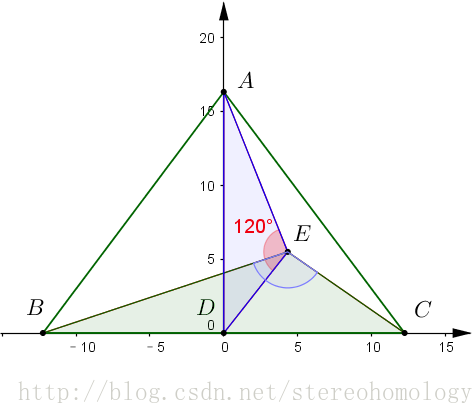
对这个问题，先建立如下图的坐标系：

可以容易（计算量很小、难度初等）得到如下点的坐标：

$$A:(0,\dfrac{49}3),B:(-\dfrac{49}4,0),C:(\dfrac{49}4,0)$$

然后假设 $E: (x,y)$。

根据已知，容易知道 $\cos\angle AED=-\dfrac{1}2$ 以及$\cos\angle BEC=-\dfrac{3}5$,

对图中的两个三角形$\Delta BEC$ 和 $\Delta AED$ 以$E$ 为顶点的角及其对边，使用余弦定理，整理可以得到下面两个看上去吓人的式子：

$$\left\{ \begin{array}{rl} 6 x^2+6 y^2-98 y+\sqrt{\left(9 x^2+(49-3 y)^2\right) \left(x^2+y^2\right)}&=0 \\ 80 x^2+80 y^2+3 \sqrt{256 x^4+512 y^2 x^2-76832 x^2+256 y^4+76832 y^2+5764801}&= 12005 \\ \end{array} \right.$$

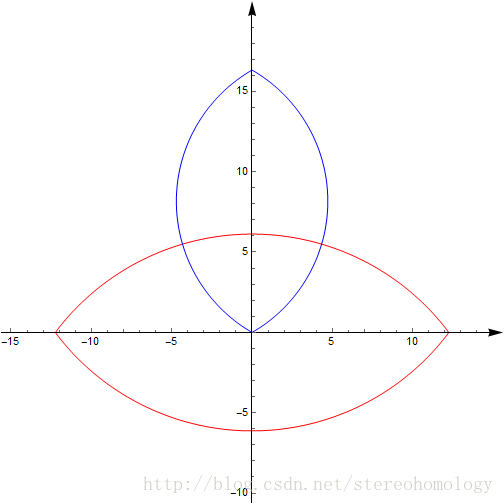
它们对应于两个曲线的隐函数方程，画出来是这样的：

之所以说方法是“暴力”的，主要体现在，如果考场上用初等方法，到这里就该差不多放弃了，但现实中可以用一系列的符号计算工具轻松求解。可以用的工具包括，Maxima, Axiom, Mupad in matlab, maple, mathematica等等。于是得到跟曲线图上两个交点对应的两个解：

$$x=\pm\dfrac{5 \sqrt{3}}{2},y=\frac{11}{2}$$

从坐标看也能发现， $E$ 在 $\Delta ABC$内可以有互为镜像的两个位置，它们都能满足题设条件。

回到初等几何能够轻易求解的内容： $DE=\sqrt{x^2+y^2}=7$

当然，如果严格用Geogebra作图，把$E$ 画出来之后测量线段 $DE$，会发现长度刚好是 7 <script type="math/tex" id="MathJax-Element-15">7</script> ( 但Geogebra给出的测量都是近似值，只有确认是初等几何竞赛题、了解命题的一贯作风，才能判断出7不是近似值，而通常是精确值，所以这种办法有参考作用但不严格）