综述
刚开始接触机器学习就提到了正则化,一直没有把里面东西搞清楚。今天决定写一篇关于正则化的文章将里面的问题讲讲清楚。
从多种角度认识正则化
正则化的作用
正则化作用补充
正则化参数选择
从多种角度认识正则化
1、贝叶斯角度的正则化
LR正则化对应数据先验的分布。比如L1(LASSO)先验对应高斯分布,L2(Ridge)对应拉普拉斯分布。现在通过一个案例说明LR正则化代表对模型参数引入先验分布,来看线性回归:
y=Wx+ϵ
y
=
W
x
+
ϵ
,之前线性回归已经了解到
y−Wx=ϵ
y
−
W
x
=
ϵ
对于
ϵ
ϵ
服从高斯分布因此:
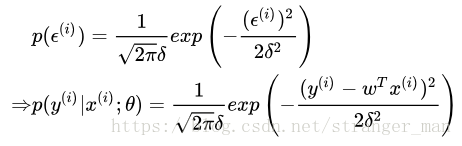
接下来就是按照最大似然的方法求解似然函数啦,但是这一次我们贝叶斯公式对参数
w
w
添加一个先验。这个先验可以从似然函数的共轭先验中选(共轭先验最后一部分)择均值0,方差为的高斯先验。得到新的似然(或者成为后验)函数:
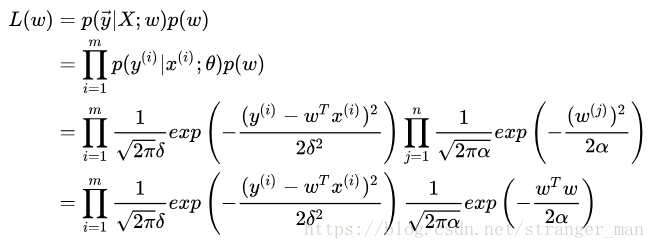
对似然函数取对数:
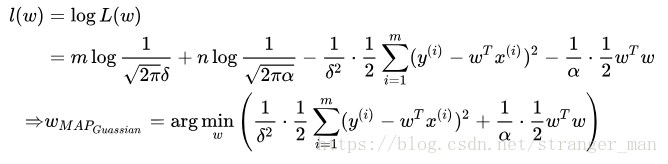
观察得到的最后一项不就是L2正则化项吗?于是我们说对参数引入高斯先验等价于进行L2正则化。相同的问题,怎么从贝叶斯角度看待这个正则化项解决过拟合问题呢?其实模型之所以出现过拟合是因为学习到了过多噪声,也就是模型过于复杂。通过引入一个先验知识可以在一定程度上抑制模型的复杂度,让模型在一个预先定义的模型框架学习。
上文说完了L2接下来再来看一下L1,首先看一下拉普拉斯分布是个什么鬼?
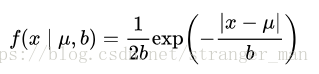
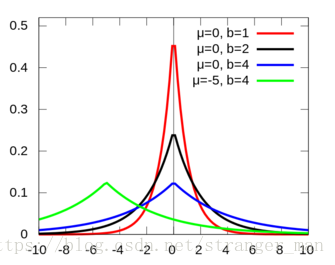
观察一下发现与正态分布间的图像很像,有兴趣的可以去查一下与正态分布的关系。我们重复L2中的推导很容易得到:
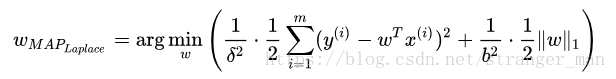
观察表达式的右侧得到了L1的正则化项。我们知道贝叶斯模型中可以有效的缓解过拟合问题,通过前面的分析发现,其实贝叶斯学派中对也是有过拟合处理的模块的。贝叶斯的似然函数相当于损失函数,先验分布相当于正则化项。想深入了解的同学可以查看这篇文章——Lazy Sparse Stochastic Gradient Descent for Regularized Mutlinomial Logistic Regression
2、结构风险最小化
这里的想法很简单,就是为了缓解风险加上一个正则化项,通过添加一个正则化项降低参数的大小,让各个参数起的作用小点那么整体的模型趋于简单。但是通过这个角度我们可以很好的解释不同正则化项起的作用。
正则化的多种作用
我们经常使用的正则化参数有L0,L1,L2三种,其中L0与L1作用相似,但是L1更易于优化所以我们一般直接使用L1,本文也就常用的两种正则化项进行说明。
1. L1——(Lasso regularization)的作用
L1范数是指向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)。为什么L1范数会使权值稀疏?任何的规则化算子,如果他在
wi=0
w
i
=
0
的地方不可微,并且可以分解为一个“求和”的形式,那么这个规则化算子就可以实现稀疏。这说是这么说,
w
w
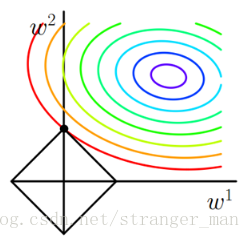
的L1范数是绝对值,在w=0处是不可微,但这还是不够直观。通过一张大家都见过但是没见过有人讲清楚的图的说明一下。
在说明这张图之前我们先来分解一下原来的似然函数,我们可以把正则化看做是损失函数的一个约束。这样逆推拉格朗日乘子法得到如下表达式:
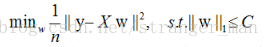
这样把又表述一个带约束的线性规划问题。但是问题的目的一定要清晰就是通过调整参数
w
w
的值来得到最小化的优化目标值。以二维问题为例,将两个方程分别画在一个以为坐标轴的平面内,其中黑色方框表示约束条件的形状。右上角一圈一圈的是损失函数的图像,损失函数是凸函数所以越往外层是函数值增大的方向,图中的方向选择等高线的法向量方向。
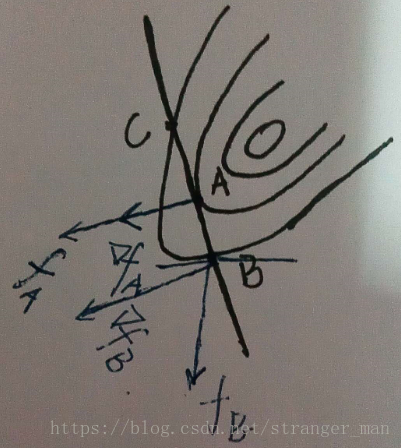
现在的问题就转化成了求解两个图像的交点问题,因为参数值没有确定我们仅能构建出一个大致的形状,通过求解出交点后才可以确定最终图像的精确模样。那么为什么最有解一定在约束图像的顶点处呢?(在凸优化课程中有对于这一命题的详细论证,感兴趣的可以查看Boyd的书)我们看一个案例:
观察上图,黑色的直线表示约束方程,方程与等高线相切于A点
fA
f
A
表示A点的法向量方向也就是函数值增大的方向,
∨fA
∨
f
A
表示A点的梯度方向,梯度方向表示损失函数在这一点坡度最大的方向。观察图中的B点,
fB
f
B
表示B点的法向量方向,
∨fB
∨
f
B
表示该点的梯度方向。B点所处的等高线要高于A点,也就是A点的得到的损失函数值要小于B点。我们的目标就是要最小化损失函数,所以A点要比B好的多。但是A点是不是最终的解,这里先给出答案——是的,是最好的点。观察A、B两点的等高线法向量方向和梯度方向有什么不同呢?A点法线和梯度共线了!B点成为一个夹角了!也就是说当法向量与梯度方向共线了这个点就是我们所要求解的点。也就是说当法向量与梯度方向存在夹角时就还有优化的空间,上图中如果在A,B两点所在的等高线间再加入一条等高线并在等高线上再选一点D发现,D的法向量与梯度的夹角又变小了,我们不断的优化一直到法向量与梯度的夹角为0时获得了最好的结果。
那好现在重新回头来看这个问题,现在再添加一条登高线(勿喷):
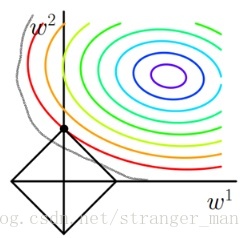
新添加的等高线,与约束区域有多个交点,用上文分析的方法发现只有图中的顶点时得到函数值是最小的。
终于大体说明白了为啥图中交点最小的问题。现在来看问啥L1正则可以得到稀疏解呢?观察图中最小值点的坐标
(0,w2)
(
0
,
w
2
)
发现
w1
w
1
为0,也就是得到的最优值的点只有
w2
w
2
起作用,设想在高维的情况下,会有更多的参数等于零。这样就是L1得到稀疏解的来源!换种说法就是L1范数可以自己选择重要的特征参与运算。
1. L2的作用
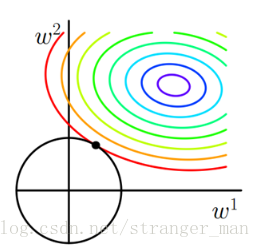
说清楚L1的作用再说L2就轻松多了。还是直接上图:
观察约束是个圆形,这个时候最优解取到坐标轴上的可能性是比较小的。所以L2正则化最大主要目的是使得各个参数趋向于0,这样会得到一条更加光滑的函数。因为一般认为参数值小的模型比较简单,能适应不同的数据集,也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程,若参数很大,那么只要数据偏移一点点,就会对结果造成很大的影响;但如果参数足够小,数据偏移得多一点也不会对结果造成什么影响,专业一点的说法是『抗扰动能力强』。
接下来通过公式再来看一下这个问题,最小化损失是通过梯度下降一步步求解的,我们先看L2的梯度更新公式:
没有L2正则项时,参数更新公式没有公式右侧的第一项。加入正则化后,发现参数先乘上一个小于1的数然后再减去后面的一坨。这样参数下降的就更多了。而只有L1正则时,
公式后面仅仅是个很小的常数因子,对参数的下降作用并不明显。
正则化的作用补充
正则化参数选择
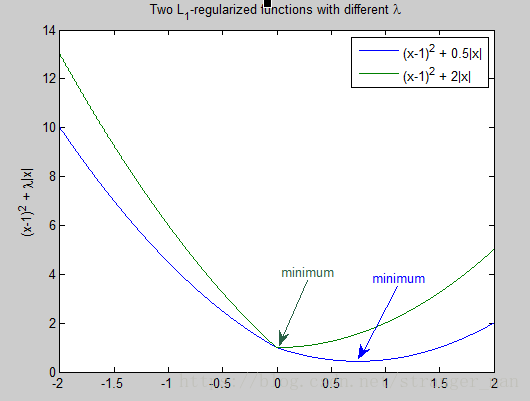
通常越大的λ可以让代价函数在参数为0时取到最小值。下面是一个简单的例子,这个例子来自Quora上的问答。为了方便叙述,一些符号跟这篇帖子的符号保持一致。
假设有如下带L1正则化项的代价函数:
其中x是要估计的参数,相当于上文中提到的 w w 以及. 注意到 L1 L 1 正则化在某些位置是不可导的,当 λ λ 足够大时可以使得时取到最小值。如下图:
分别取 λ=0.5和λ=2 λ = 0.5 和 λ = 2 ,可以看到越大的 λ λ 越容易使时取到最小值。
L2正则化参数;参考图2,λ越大,L2圆的半径越小,最后求得代价函数最值时各参数也会变得很小。








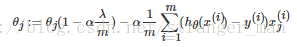













 228
228











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








