四色猜想与连连看

四色猜想与连连看

前言： 

         1. 以下仅是个人对于四色猜想论证的思路，本人并未证明四色猜想，且其以下过程或结果可能是不严谨、甚至是错误的。

         2. 本人希望通过这篇文章能够起到抛砖引玉的效果，给予他人启发。

        3.  另如有其它文章其内容与本文雷同，则纯属巧合，特此说明。

正文：

         参考连连看游戏，任意两个图案如相同，且无其它图案分隔，则可以消除。那么四色问题可转换为任意两个相同颜色之间是否一定有其它颜色分隔，即需要多少颜色可以达到任意两个相同颜色的图形之间一定存在不相同颜色的图形进行分隔。

         但在连连看游戏中，每个图案的形状大小都固定，即都是等边的正方形，故只需两种颜色即可达到分隔的作用，但实际情况是图案的形状与大小都不固定。

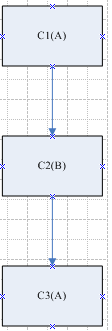
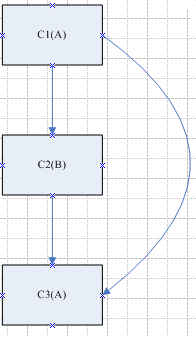
         先假设我们有A、B两种颜色分别对C1、C2、C3这三个图形进行着色，那么我们很容易画出以下图案：

            

         以上三个图案中由于C1、C2、C3形状固定， 故用两种颜色即可做到两个相邻图形的颜色不一致，等同于连连看游戏中的图案。

 

         我们先将以上图案转换为树，具体如下：

           

     以上树表示C1先用颜色A着色，之后与其相邻的C2用颜色B着色，最后与C2相邻的C3用颜色A着色。(其树枝可认为是连通路径，即两个图案可相邻)

     但实际情况中，图形的形状不固定，那是否可在上述的树结构中进行修改，将形状不固定这一因素体现在以上模型中。

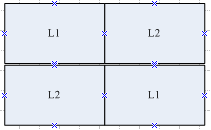
     我们还是从连连看游戏出发，请看下图：

         

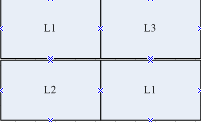
       假设某个连连看游戏中，有四个方块，且这四个方块满屏，即没有剩余空间可放入第五个图案。此时L1与L2图案都无法消除，因都被另一个图案分隔。

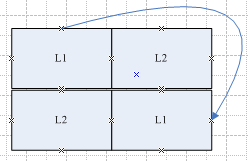
       则形状不固定可视为有一隐藏路径，可连接两个相同的图案，如下所示：

           

       将L1对应之前树中的C1、C3图形，则可看作C1、C3围绕C2旋转，结果C1、C3可以相碰，如下所示：

            

       上述旋转（左图）在连连看游戏中则是某个L1方块发生变形，使其同时与另两个图案分别为L1、L2的方块相邻（右图），对于之前的树结构可认为存在C1、C3连通路径，如下图：

           

      此时由于C1与C3之间有一连通路径，故在两色情况下，必定存在两个相邻图形颜色相同的颜色。

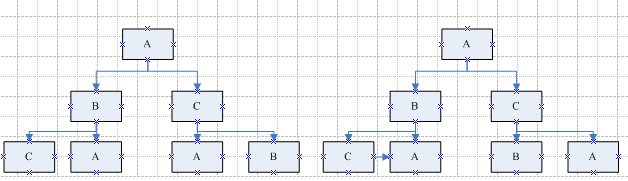
      现假设有A、B、C三种颜色，用以上模型对三色进行验证，具体如下：

          

       以上是三色时图形着色情况，即先任选一个图形进行用A着色，则相邻图形可用B或C颜色着色，再相邻图形可用C、A或A、B颜色着色。

       对于右图，根据两色时的推论，已存在连通路径，即：

         

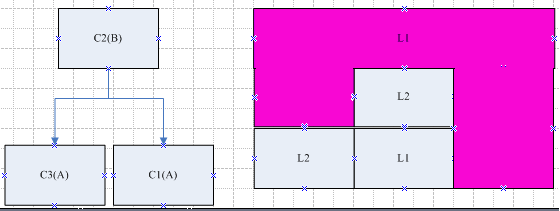
      对于左图我们还是根据连连看游戏进行说明，假设在连连看游戏中存在三种图案L1、L2、L3，则将两色时的四个方块的图案稍作变化，如下图：

           

       在上图中我们将某个方块的图案变为了L3，其实根据两色时的情况，某个图案为L1的方块发生形状变化时，依旧存在连通路径，将此情况体现在刚才左图的树结构中：

            

        上图已说明在三色时，总存在路径可使两个颜色相同的图形连通(通过图形变化实现)，那么我们可以提出以下推论即：

        任一不是顶点或叶子节点的节点T，如T的父节点的颜色与T某个最左或最右子节点的颜色相同，则存在相同颜色的图形相邻的情况。

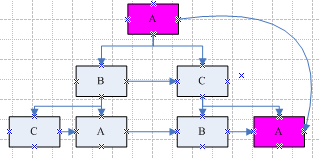
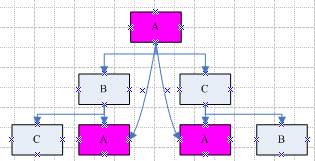
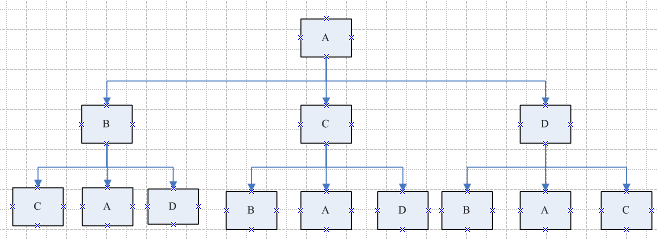
        最后假设有A、B、C、D四种颜色，使用以上模型进行演示：

           

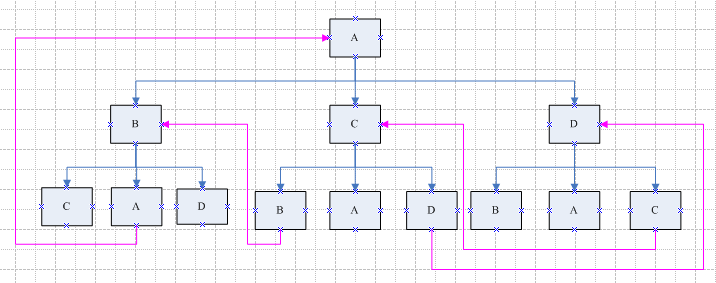
         在四色的情况下，我们发现没有符合上述推论，即四色时不存在相同颜色的图形相邻的情况，且此树可以无穷迭代，即：

             

         由上图可知，任意图形被三种不同颜色的图形包围，且可无穷迭代，使相邻两个图形的颜色始终不一致。